б) Термодинамическая и информационная энтропии

Термин "энтропия" заимствован из термодинамики и статистической физики. Известно, что движения молекулы в жидкостях и газах подчинены вероятностным законам распределения. Для характеристики состояния системы, состоящей из молекул, вводят понятие энтропии. Формула для нее имеет тот же вид, только под величиной pi понимается вероятность существования в некотором состоянии i-й подсистемы исходной системы. Так же как и в теории информации, в статистической физике эта величина является мерой необратимости процесса преобразования тепловой энергии в механическую. Если процесс обратимый, то его энтропия равна нулю. В необратимых процессах величина энтропии определяет энергию, потерянную безвозмездно при ее преобразовании.

В теории информации имеют место такие же закономерности, что и в термодинамике [Л. 50]. Наибольший интерес с точки зрения теории информации представляет статистическая трактовка второго начала термодинамики, данная Больцманом: во всякой изолированной системе происходят такие изменения, которые приводят систему к ее наиболее вероятному состоянию.

Аналогичные закономерности имеют место в кибернетике при исследовании больших систем. Так, работа телефонной сети города может быть исследована как набор систем массового обслуживания, и такая большая система стремится к наиболее вероятному состоянию. Необратимые процессы В замкнутых системах приводят к наиболее вероятному состоянию, при этом возрастает энтропия, которая становится максимальной в равновесном состоянии системы. Поэтому вполне естественно предположить, что энтропия является функцией вероятности состояния системы, т. е.

Можно показать [Л. 50], что

Величину К достаточно определить для любого частного случая, так как для всех систем она должна иметь одно и то же значение:

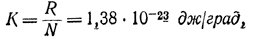
т. е. равна постоянной Больцмана. Теперь, если в формуле (6-6) положить аддитивную постоянную равной нулю, то выражения для термодинамической S и информационной Н энтропий совпадут с точностью до множителя, т. е.

Разницу в множителях можно рассматривать как результат разных единиц измерения термодинамической и информационной энтропии. Если число возможных состояний в системе N и все они равновероятны, то N=1/р и формулы (6-7) и (6-8) перепишутся в виде

Иногда в физике величину N называют числом популяций в системе (числом микросостояний).