7-3. Понятие избыточности сообщения

Выделение полезного сигнала из шумов - одна из основных проблем передачи сообщения при наличии помех. Чтобы восстановить полезный сигнал, приходится в ряде случаев передавать дополнительные символы, дополнительные значения сигнала, т. е. вводить в сообщение избыточность.

Можно привести много примеров применения этого метода. Так, в сообщении "Весна пришла" можно исключить две последние буквы и передать "Весна приш..", но из-за больших шумов может получиться искажение, например "Весна прошла". Для гарантии надо передать "Весна пришла, но еще не кончилась".

По теореме Котельникова непрерывные сообщения можно передавать дискретными значениями минимальным количеством N=2f_ct₀, однако при наличии помех следует брать N>2f_ct₀. Эти особенности сообщений и характеризуют избыточность R.

Пусть сигнал из n символов содержит количество информации I. Если он обладает избыточностью, то его можно передать меньшим количеством символов n₀. При этом если ввести количество информации на один символ сообщения I₁ то во втором случае оно будет больше:

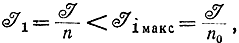
и очевидно, что

За меру избыточности принимают относительное удлинение сигнала при данной избыточности

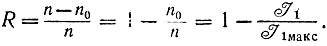
Очевидно, могут встречаться различные случаи. Так, если требуется устранить избыточность, вызванную статистическими связями между символами, сохранив при этом разную вероятность появления символов, с помощью количества информации на один символ

то можно ввести избыточность, обусловленную связью между символами:

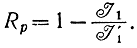
Кроме этой может быть избыточность, вызванная не экстремальным распределением символов. Известно, что при конечном числе символов m максимальная информация на символ получается при равномерном их распределении и равна I₀=log m. Поэтому избыточность, вызванная не экстремальностью распределения,

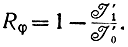
Полная избыточность

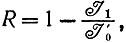
где I₁- информация на один символ при наличии связей и не экстремальности распределения символов. Рассмотренные характеристики частной избыточности связаны между собой соотношением

Если частные избыточности малы, то

и