7-2. Пропускная способность каналов связи

Рассмотрим канал связи, представленный на рис. 5-1. На его передающий конец подается сигнал x(t), который поступает на вход приемника в искаженном шумом n(t) виде y(t) [Л. 47, 53]. Введем понятие пропускной способности канала связи. Пропускная способность канала связи определяется как максимальная величина относительной информации выходного сигнала относительно входного:

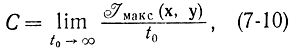
где I(x, y) - относительная информация, задаваемая формулой (7-8), причем все сигналы рассматриваются как эквивалентные дискретные (рис. 7-1), так что

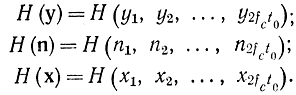
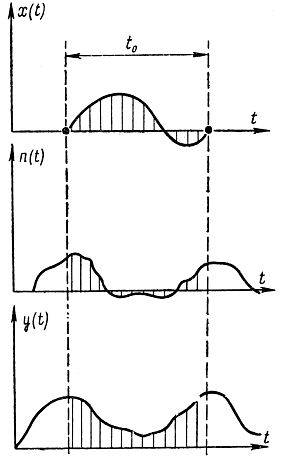
Рис. 7-1. Пояснения к определению пропускной способности канала связи

Иногда величина 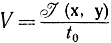называется скоростью передачи информации по каналу связи. Эта величина равна количеству относительной информации, передаваемой в единицу времени. За единицу времени при дискретном канале связи удобно считать время передачи одного символа. В этом случае в формулах для скорости передачи информации понимают энтропии и количества информации на один символ. Для непрерывных каналов связи используются две единицы измерения или обычная единица (к примеру, секунда), или интервал времени между отсчетами 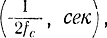, в этом последнем случае в формулах понимаются дифференциальные энтропии на один отсчет (или степень свободы). Нередко в руководствах специально не указывается, какая конкретно из двух единиц применяется. В связи с этим часто используют другую формулу для средней скорости передачи информации

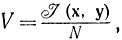
где N=2f_ct₀. Если отсчеты независимы, то V=I₁(х, y). Очевидно, что с помощью величины V пропускная способность канала связи может быть определена по формуле

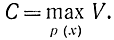
Для энтропии шума можно написать:

где

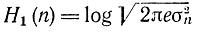
- энтропия шума на один отсчет для нормального шума.

Аналогичные формулы можно записать для нормальных сигналов х и y.

Формулу (7-10) для единицы отсчета можно записать в виде

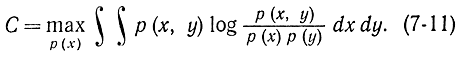
Смысл этого определения требуется разъяснить. Отметим, что максимум здесь взят по множеству распределений вероятности входных сигналов при неизменном шуме, которое предполагается заданным. В частном случае это множество распределений может состоять из одного нормального, как это часто и считается.

Если пропускная способность одного канала связи больше, чем другого (С₁>С₂) при остальных одинаковых условиях, то физически это означает, что в первом случае совместная плотность распределения вероятности входного и выходного сигналов больше, чем во втором, так как с помощью формулы (7-11) нетрудно убедиться, что пропускная способность определяется в основном величиной совместной плотности распределения вероятности. Если относительная информация (или энтропия) выходного сигнала относительно входного больше, то канал обладает большей пропускной способностью. Ясно, что если шумы возрастают, то пропускная способность падает.

Если вероятностная связь выходного и входного сигналов пропадает, то

и в формуле (7-11) логарифм и, следовательно, пропускная способность становятся равными нулю.

Другой случай, когда

стремится к нулю, требует детального рассмотрения, так как log р(х,y) стремится к - ∞. Если р(y)→0, то

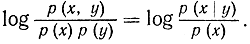
Рассуждения можно продолжить следующим образом. Так как вероятность появления выходного сигнала стремится к нулю, то можно положить, что вероятность появления сигнала х не зависит от y, т. е.

и

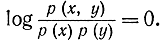
В этом случае пропускная способность равна нулю, что согласуется с физической интерпретацией, т. е. если на выходе канала связи не появляется никакого сигнала [ни полезного x(t), ни шумов n(t)], это означает, что в канале есть "пробка" (разрыв). Во всех остальных случаях пропускная способность отлична от нуля.

Естественно определить пропускную способность канала связи так, чтобы она не зависела от входного сигнала. Для этого введена операция максимизации, которая в соответствии с экстремальными свойствами энтропии чаще всего определяет входной сигнал с нормальным законом распределения. Покажем, что если x(t) и n(t) независимы и y(t)=x(t)+n(t), то

где Н(y) и Н(n) - дифференциальные энтропии принимаемых сигнала и шума. Условие (7-12) означает линейность канала связи в том смысле, что шум просто добавляется к сигналу как слагаемое. Оно непосредственно следует из

Так как x и n статистически независимы, то

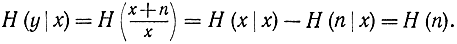
Подставив это соотношение в предыдущее, получим (7-12). Очевидно, если шум аддитивен и не зависит от входного сигнала, то максимальная скорость передачи сообщений по каналу связи (максимальная пропускная способность) достигается при maxН(y), так как

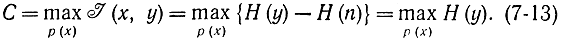
Рассмотрим гауссов канал связи, исходя из следующих предположений: ширина полосы частот канала ограничена частотой f_с; шум в канале - нормальный белый со средней мощностью на единицу полосы S_n=S_n²; средняя мощность полезного сигнала Р_x; сигнал и шум статистически независимы; выходной сигнал равен сумме полезного сигнала и шума.

Очевидно, что в соответствии с формулой (7-4) пропускная способность такого канала определится как

Далее согласно первым двум условиям имеем для энтропии на единицу времени (t₀=1)

Так как сигнал и шум статистически независимы, то они не коррелированы между собой, поэтому средняя мощность суммарного сигнала

В соответствии с формулой (7-13) необходимо найти максимум энтропии сигнала y(t) на один отсчет при заданной средней мощности. В силу экстремальных свойств энтропии (см. гл. 6) сигнал y(t) должен быть распределен нормально. Белый шум в полосе f_c эквивалентен сигналу в этой же полосе со спектральной плотностью S, если равны их средние мощности, т. е.

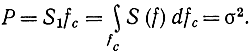
Действительно, для нормального сигнала была доказана формула для энтропии на один отсчет

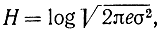
из которой видно, что характер сигнала (белый шум или нет) здесь безразличен, важна только дисперсия. Из физических соображений очевидно, что энтропия белого шума будет максимальной при прочих одинаковых условиях (законе распределения), так как в белом шуме отдельные отсчеты независимы. При этом неявно предполагается, что непрерывный сигнал заменяется эквивалентным дискретным сигналом, отсчеты которого независимы. Поэтому можно считать, что сигнал y - белый шум в полосе f_c. Из формулы

следует, что и сигнал х(t) имеет вид белого шума. Обозначив

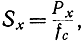
запишем:

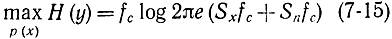
и, вычитая из формулы (7-15) формулу (7-14), получаем:

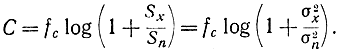
Это - формула Шеннона для пропускной способности, реализуемой в гауссовом канале связи. Практически пропускная способность всегда меньше главным образом из-за различных статистических свойств сигнала и помех.

Передача сообщений возможна и в случае, когда P_n>P_x,только пропускная способность будет мала. В случае малого отношения сигнал/шум можно функцию логарифма разложить в ряд Маклорена

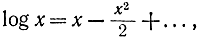
в результате

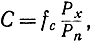
т. е. при малом отношении сигнал/шум пропускная способность пропорциональна этому отношению. При большом отношении сигнал/шум

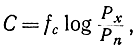
т. е. пропускная способность пропорциональна логарифму отношения сигнал/шум.

В любом случае для увеличения пропускной способности необходимо увеличивать мощность полезного сигнала и уменьшать уровень шумов на входе канала.