в) Корреляционный метод приема

Вычисление корреляционной функции позволяет выделить синусоидальное напряжение в шумах, даже если последние в 100-1 ООО раз превышают амплитуду синусоиды. Рассмотрим случай с полезным сигналом х(t)=aсosω₀t и стационарной помехой ξ. Корреляционная функция полезного сигнала - косинусоиды (рис. 7-3):

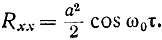
Корреляционная функция помехи затухает со временем. В случае независимости полезного сигнала и помехи корреляционная функция суммарного сигнала определяется как

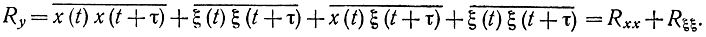
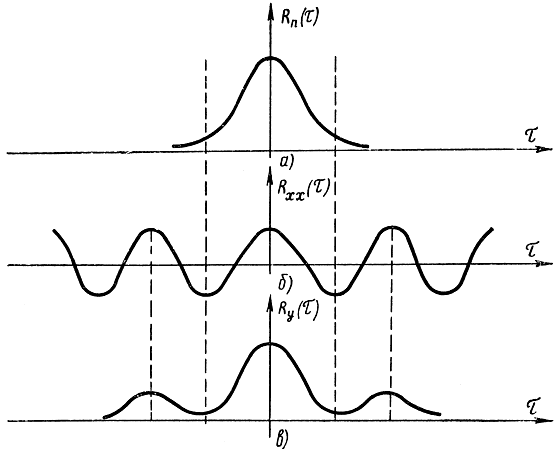
Рис. 7-3. Корреляционные функции шума (а), периодического (б) и суммарного (в) сигналов

Но, очевидно, необходимо долго ждать, и тем дольше, чем медленнее затухает функция корреляции помехи (чем уже спектр) и чем больше мощность помех

Однако в отличие от предыдущего здесь теряется начальная фаза синусоиды.