7-5. Общая теория помехоустойчивости
Геометрическая интерпретация в теории информации широко используется для представления любых сообщений и сигналов. Чаще всего к ней прибегают в случае непрерывных сообщений. Различают пространства сообщений и сигналов [Л. 48, 56]. Если сообщение дискретно, то при конечном времени передачи оно характеризуется конечным числом своих значений, если сообщение непрерывно, то согласно теореме Котельникова его можно полностью определить дискретными значениями. В силу этого каждое сообщение можно представить некоторой точкой в пространстве. Число измерений пространства равно числу N отсчетов или степеней свободы. Система координат - прямоугольная. Вся совокупность сообщений в пространстве сообщений отражается некоторым объемом. Как уже указывалось, для передачи сообщений их необходимо преобразовать в сигналы. Например, в сигналы преобразуются сообщения, поступающие в виде давления воздуха у микрофона р=f(t) (телефония); в виде тока звуковой частоты, повторяющего форму f(t) (телефония - сигнал после микрофона); тока высокой частоты, амплитудно-модулированного по закону f(t) (радиосвязь); в виде освещенности последовательно передаваемых элементов (фототелеграфия, телевидение).
Если сообщение непрерывно, то, как правило, сигнал тоже непрерывен.
Для сигнала тоже вводят пространство сигналов размерностью N.
С геометрической точки зрения процесс передачи заключается в том, что каждой точке пространства сообщений должна однозначно соответствовать определенная точка пространства сигналов. В пространстве сообщений точки располагаются неравномерно с разной плотностью. Распределение точек определяется статистикой сообщений. При преобразовании пространства сообщений в пространство сигналов распределение точек меняется. Пусть u - сообщение, передаваемое с помощью сигнала, x - принятый сигнал. В общем случае они связаны некоторым преобразованием x=ψ(u). Символ ψ - преобразование, которое не обязательно задается аналитически. Однако для простоты суждений предположим, что ψ - некоторая функция.
Допустим, имеется функция сообщения u(t), квантованная на m. Уровней, с пределами изменения 0<u<uмакс. В случае амплитудно-импульсной модуляции можно написать:
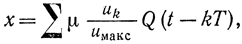
где uk=(kT); μ≤1 - глубина модуляции; Q(t) - функция, описывающая отдельный импульс. Для случая, когда та же функция
сообщения преобразуется в сигнал с фазо-импульсной модуляцией, имеем:
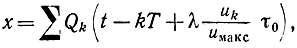
где λ≤1 - глубина фазовой модуляции; τ0 - наибольшее смещение импульсов, которое можно принять равным T, если пренебречь длительностью импульса по сравнению с периодом чередования Т.
Таким образом, процесс передачи сообщений можно представить в виде, показанном на рис. 7-5. При передаче сообщения и преобразуются в сигналы х, т. е. пространство U преобразуется в пространство X. На приемном конце из сигналов х вновь восстанавливается сообщение v, т. е. пространство X преобразуется в пространство V. При передаче на сигнал накладывается помеха, которая тоже представляется некоторым вектором. В отсутствие помехи
v=ψ-1(х)=ψ-1[ψ(u)]=u.
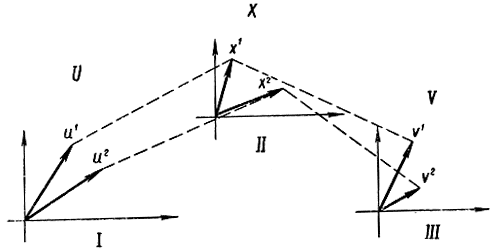
Рис. 7-5. Геометрическая интерпретация передачи сообщений. I - пространство передаваемых сообщений; II - пространство сигналов; III - пространство принимаемых сообщений
Однако помеха существует, и в результате ее воздействия происходит искажение сигнала. Можно построить приемник, который будет воспроизводить сообщение v1=u1 всякий раз, когда конец результирующего вектора х=х1+ξ, где помеха ξ ближе к концу вектора- сигнала х1, чем к концу ближайшего вектора-сигнала х2. Такой приемник по Котельникову называется идеальным. Его действие характеризуется тем, что пространство X оказывается разбитым на области, границы которых представляют собой места точек, равноотстоящих от точек различных сигналов (концов векторов). Ошибка приема идеальным приемником, т. е. замена переданного сообщения другим, возможным, происходит лишь тогда, когда результирующая точка, представляющая сигнал с наложенной помехой, переходит границу данной области и оказывается в соседней. Вероятность появления такого события характеризует помехоустойчивость связи. Для идеального приемника вероятность ошибки оказывается наименьшей, а, следовательно, помехоустойчивость - наибольшей. По Котельникову предельно достижимая помехоустойчивость называется потенциальной. Очевидно, что помехоустойчивость будет тем больше, чем больше расстояние d между соседними сигналами (рис. 7-6), т. е. расстояние между концами векторов, представляющих эти сигналы. Это расстояние зависит не только от расстояния между соседними сообщениями, но и от функции преобразования, т. е. помехоустойчивость системы связи зависит от способа модуляции. Ока тем выше при данном способе модуляции, чем больше d.
Условие правильной передачи сообщения u1 при идеальном приемнике следующее:
|х- х1|<|х-х2|;
Здесь ξ - помеха; х1 - сигнал, соответствующий сообщению u1; х=х1+ξ - сигнал х1, искаженный аддитивно независимой от сигнала.
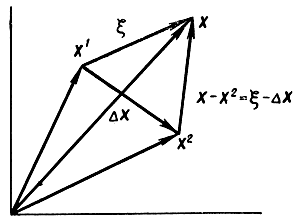
Рис. 7-6. Пояснения к вывода соотношения для идеального приемника
Условие безошибочного приема можно записать в виде
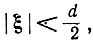
где
d=|Δx|.
Учитывая, что
х=ψ(u)
и
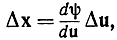
получаем:
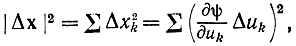
откуда, усредняя, находим:
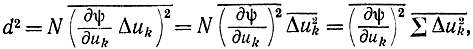
где N - число дискретных отсчетов сигнала. Здесь предполагается, что частные производные от функции ψ по координатам и приращения по ним - независимые величины. В общем случае
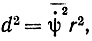
где r - среднее расстояние между сообщениями в пространстве сообщений. Если сигнал квантован, то минимальное расстояние между сигналами
rмин=δ
где δ - расстояние между уровнями квантования, поэтому
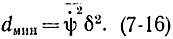
Вероятность ошибки
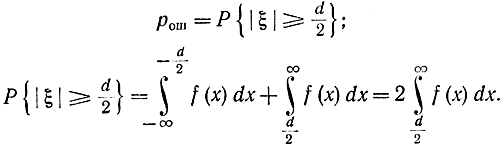
Учитывая, что для нормально распределенного шума
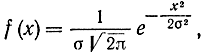
где σ2 - дисперсия шума (помехи), в соответствии с формулой (7-16) получаем:
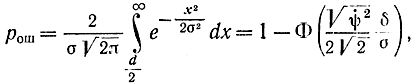
где интеграл вероятности, для которого составлены таблицы (см. приложение 1), равен:
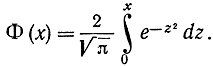
При этом следует учитывать, что
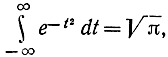
т. е.
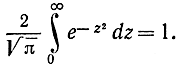
Пример 7-1. Рассмотрим пространства сигналов для трех случаев (рис. 7-6) модуляции:
амплитудно-импульсной (АИМ);
импульсной модуляции по длительности (ДИМ);
фазо-импульсной (ФИМ).
Допустим, что с помощью этих трех видов сигналов передается ансамбль из трех сообщений: 1, 2, 3. Необходимо выбрать координаты в пространстве сигналов. Выберем их в соответствии с рис.. 7-7. Для сравнения этих трех случаев сравним средние энергии сигналов (табл. 7-1). За единицу примем мощность одного импульса единичной амплитуды.
Для уравнивания средних мощностей возьмем за единицу линейного масштаба величину, обратно пропорциональную корню квадратному из средней мощности. В результате получим отношения для длин масштабов
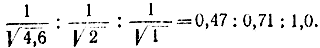
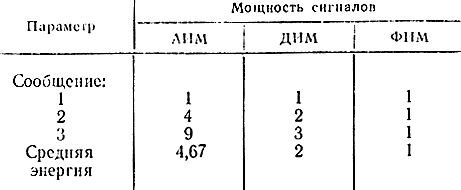
Таблица 7-1
Когда передается сообщение, то в пространстве сообщений вектор описывает некоторую линию сообщений. Под линией сигнала понимается совокупность точек сигнала при передаче сообщения. Можно сказать, что чем длиннее линия сигнала, тем более помехоустойчива система. Фактически величина
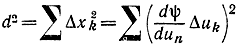
есть приращение квадрата длины линии сигнала. Очевидно, помехоустойчивость будет больше при ФИМ.
Для нашего примера в случае АИМ: 3*0,47= 1,41;
ДИМ: 3*0,71 = 2,13;
ФИМ: 3*1 = 3.
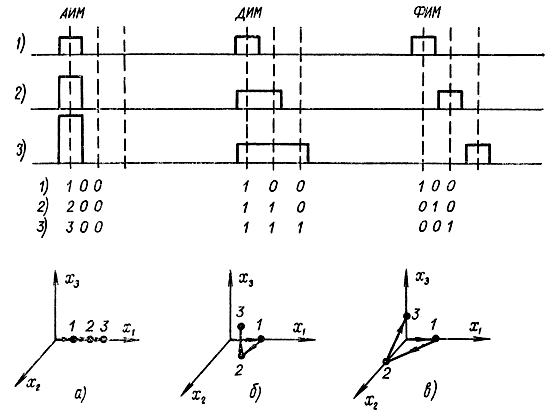
Рис. 7-7. Примеры пространства сигналов для разных случаев модуляции. а - АИМ; б - ДИМ; в - ФИМ
В общем случае N-мерного пространства сигнал с фазовой модуляцией изображается некоторой сферой. При непрерывном изменении
сообщения вектор описывает на этой сфере некоторую кривую. В наших примерах мы имеем дело с линией сигналов. Если сигнал квантован, то непрерывная линия заменяется совокупностью точек. Пояснить резкое изменение помехоустойчивости для ФИМ, начиная с некоторого значения помехи, можно следующим образом (рис. 7-8). Для ФИМ все точки сигналов лежат на сфере, квадрат радиуса которой равен средней энергии сигнала. Если помеха возрастает, то она может охватить всю сферу сигнала и помехоустойчивость резко падает. При АИМ включение точек сигнала в сферу помехи происходит постепенно и резкого изменения помехоустойчивости нет. Говорят, что резко порога помехоустойчивости при АИМ не наблюдается.
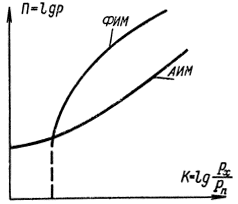
Рис. 7-8. Зависимость помехоустойчивости от превышения сигнала над шумом случаев ФИМ и АИМ.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'