8-2. Оптимальный код Шеннона - Фено

Для построения оптимального кода Шеннона - Фено все символы алфавита располагаются в порядке убывания вероятности их появления. Символу, встречающемуся чаще всего, присваивается наиболее короткая комбинация. В английском языке чаще всего встречается буква E(р=0,13). Этой букве отведена самая короткая кодовая комбинация - точка. В русском языке наиболее повторима буква О (р=0,11), но ей отведена далеко не самая короткая кодовая комбинация - три тире. В этом смысле для русского языка принятая система кодирования в азбуке Морзе не является оптимальной.

Оптимальным считается код, имеющий минимальную среднюю длину

причем

где суммирование выполняется по всем символам алфавита; l_k - длина кодовой комбинации, равная числу ее элементов, соответствующая k-y символу алфавита; p_k - вероятность появления в сообщениях данного ансамбля k-то символа; Σp_k=1.

Здесь будут рассмотрены только двоичные коды, хотя все изложенное справедливо для троичных и других кодов.

Пример 8-1. Рассмотрим табл. 8-1, в которой приведен алфавит, состоящий из шести Символов.

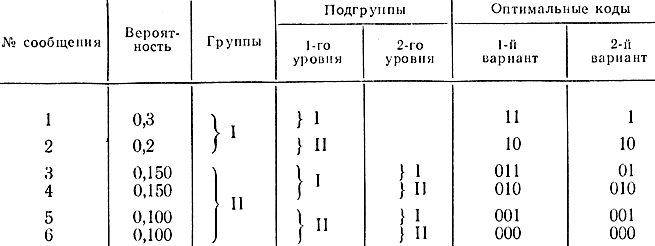
Таблица 8-1

Во втором столбце даны вероятности появления символов, в третьем, четвертом, пятом - разбиение на группы и подгруппы, в шестом и седьмом - кодовые комбинации, которые строятся так: все символы разбиваются на две группы, чтобы суммарные вероятности в каждой группе были примерно равны. В нашем примере в первую группу попали два первых символа, во вторую - все остальные. Первой группе присваивается символ 1 в первом слева разряде, второй -0. Далее процесс повторяется: первая группа разбивается на две подгруппы примерно с одинаковыми суммарными вероятностями и т. д. То же самое делается со второй группой. Процесс деления заканчивается, когда в каждой подгруппе остается по одному символу. Графически этот процесс можно изобразить в виде ветвящегося дерева (графа), представленного на рис. 8-3. В кодовой комбинации каждой левой ветви из какой-нибудь вершины соответствует единица, правой - нуль. Каждому законченному коду соответствует так называемая висячая вершина на вертикальных линиях, обозначающих различные вероятности.

В предпоследней колонке табл. 8-1 представлен оптимальный код. Его средняя длина l_ср=2,5. Очевидно, что возможны модификации рассмотренной процедуры. Так, в последнем столбце представлен код, обладающий меньшей средней длиной, однако его составление требует более сложной процедуры (алгоритма), что затруднительно при большом алфавите, насчитывающем сто, тысяча символов.

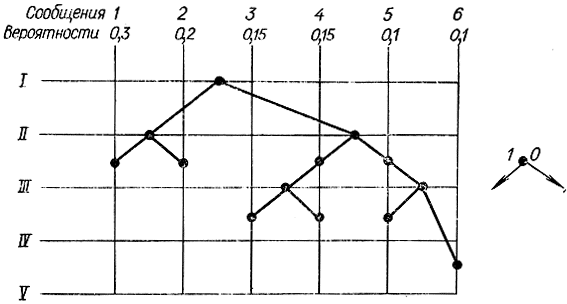
Рис. 8-3. Граф построения кода Шеннона - Фэно, требующего разделительного знака

По поводу рассмотренной процедуры составления кода можно сделать два замечания. Во-первых, с точки зрения помехозащищенности предпочтительнее передавать единицы, а не нули, так как в предположении, что единице соответствует посылка сигнала, а нулю - ее отсутствие, искажение нуля помехами более вероятное событие, чем искажение единицы. Во-вторых, одну кодовую комбинацию необходимо выделить для обозначения разделительного знака между символами, так как в противном случае, если принимается последовательность из единиц и нулей, ее невозможно правильно расшифровать, т. е. рассмотренный выше код, так же как и коды Морзе и Бодо, относится к категории кодов, требующих разделительных знаков.

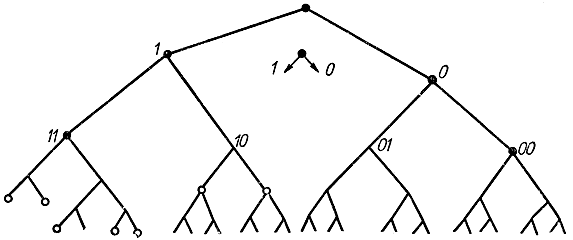
Рис. 8-4. Граф построения кода Шеннона - Фэно, не требующего разделительного знака

Однако можно построить код, не требующий разделительных знаков. Для этого уже применявшаяся комбинация не должна служить началом следующей комбинации, т. е. можно применять 10 и 001, но нельзя 10 и 100. Такую процедуру лучше всего выполнять графически с помощью дерева кода (рис. 8-4). Кружочками изображены используемые комбинации 0, 101, 100, 1111, 1110, 11011, 11010, 11001, 11000. При таком кодировании, например, последовательность 11011000110001011001110 легко расшифровывается как комбинация символов 11011-0-0-0-11000-101-100-1110.