а) Корректирующие коды Хэмминга

В простейшем случае такой код получается добавлением к кодовой комбинации единицы с тем, чтобы сумма всех единиц была четной (нечетность означает появление ошибки). Построим его на примере кода Бодо:

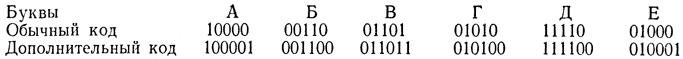
Такой код позволяет обнаружить одиночную ошибку, но не в состоянии ее локализовать и исправить.

Не только обнаружить, но и исправить ошибку можно с помощью более мощных кодов, которые строятся следующим образом. Пусть имеется n₀-значный двоичный код. Общее число комбинаций

Каждый из таких кодов отличается один от другого хотя бы одним знаком. Дополним код еще одним знаком, а число кодовых комбинаций оставим неизменным, тогда

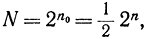
и можно так подобрать кодовые комбинации, что они будут отличаться двумя знаками. При этом будет использована только половина всех возможных комбинаций от 2ⁿ, вторая половина образует запрещенные комбинации: любое появление одиночной ошибки превращает ее в запрещенную и тем самым ошибка обнаруживается. Дополним теперь код таким количеством знаков, которое даст возможность двум кодовым комбинациям отличаться тремя знаками при неизменном числе N=2^n₀. Такой код позволит не только обнаружить, но и исправить одиночную ошибку. Действительно, если случилась одиночная ошибка в какой-то комбинации, то эта комбинация от других будет отличаться на два знака, а от своей - на один и ее легко исправить.

Определим общее число дополнительных знаков, необходимых для обнаружения и исправления одиночных ошибок. Пусть из общего числа позиций n для передачи информации используется n₀, которое будем считать фиксированным. Остальные позиции k=n-n₀ используются в качестве проверочных. Символы, которые ставятся на k проверочных позициях, определяются при кодировании проверкой на четность каждой из k групп информационных символов. Как будет далее показано, на каждой проверочной позиции при кодировании ставится 0 или 1, смотря по тому, какая сумма единиц - четная или нечетная получается при каждой из n проверок на четность. Сигнал кодируется так, чтобы в результате в каждой из n проверок получалось четное число. На приемном конце появляются на некоторых позициях единицы вместо нулей и, наоборот, нули вместо единиц. При приеме также производится проверка на четность.

Построим код, который позволял бы обнаруживать и исправлять одиночную ошибку (если произошли две ошибки сразу, код бессилен). Пусть принята кодовая комбинация с ошибкой или без нее. Произведем, в ней последовательно k проверок. После каждой проверки запишем 0, если результат свидетельствует об отсутствии ошибки на проверяемых позициях (сумма единиц четная), и 1, если результат свидетельствует о наличии ошибки (сумма единиц нечетная). Запись справа налево полученной последовательности единиц и нулей дает двоичное число. Потребуем, чтобы это число, называемое проверочным, давало номер позиции, на которой произошло искажение. Отсутствию ошибки в принятой кодовой комбинации будет соответствовать число, составленное из нулей. Проверочное число должно описывать (n₀+k+1) событий. Следовательно, число k определяется на основании неравенства

и так как n=n₀+k, то

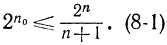
Это соотношение позволяет определить максимальное n₀ при данном n или минимальное n для данного n₀. Приведем соответствующие значения в табл. 8-2.

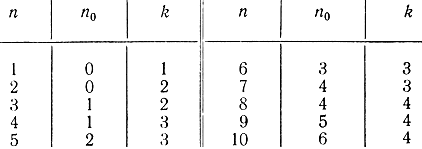
Таблица 8-2

Определим теперь позиции, которые надлежит проверить в каждой из k проверок. Если ошибок нет, то на всех проверяемых позициях

будет 0, если в низшем разряде числа стоит 1, это значит, что в результате первой проверки обнаружена ошибка. Будем при первой проверке проверять те номера позиций, двоичные представления которых имеют в первом разряде единицы, т. е.

1=1

3=11

5=101

7=111

9=1001 и т. д.

Таким образом, первая проверка охватывает позиции 1, 3, 5, 7, 9. Для второй проверки выберем такие позиции, двоичные представления которых имеют единицу во втором разряде:

2=10

3=11

6=110

7=111

10=1010

Для третьей проверки имеем:

4=100

5=101

6=110

7=111

12=1100

13 =1101

14 =1110

Такой выбор проверяемых позиций дает возможность определить номер позиции, в которой произошла одиночная ошибка. Напомним, что при каждой проверке сумма единиц должна быть четной. Если произошла ошибка на одной из позиций первой проверки, то в проверочном числе в низшем (правом) разряде появится единица, как это и должно быть. Дальнейшую расшифровку проверочного числа дает вторая проверка: если среди всех позиций второй проверки ошибок нет, то будет появляться нуль. Если на третьей позиции произошла ошибка, нарушившая четность как в первой, так и во второй проверке, то после двух проверок в двух низших разрядах появятся единицы. В третьей и следующих проверках третья позиция уже отсутствует. Каким образом, в нашем примере проверочное число равно 0011=3, что и дает номер позиции, на которой произошла ошибка. Аналогично можно убедиться, что любая одиночная ошибка на любой позиции может быть устранена проверками, дающими проверочное число, равное номеру позиции, на которой произошла ошибка.

Остается решить, какие позиции использовать под проверочные символы. Выбор для проверки позиций 1, 2, 4, 8 ... обеспечивает появление хотя бы одной их этих позиций при каждой проверке, и это позволяет независимо от знаков передаваемого числа получить при каждой проверке четное число единиц. Соответствующие проверяемые числа приведены в табл. 8-3.

Таблица 8-3

Пример 8-2. Построим код Хэмминга для n=7. Из табл. 8-3 находим, что n₀=4, k=3. Позиции 1, 2, 4 будут использоваться для передачи проверочных символов. На остальных четырех позициях разместим двоичные представления чисел от О до 15. В результате получим кодовые комбинации, приведенные в табл. 8-4.

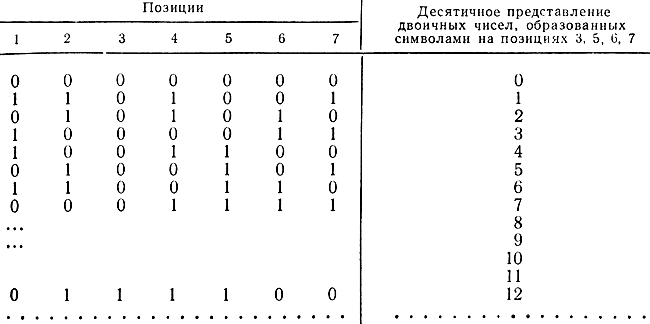
Таблица 8-4

Как видно, семизначный код с обнаружением и исправлением одиночной ошибки допускает передачу 16 сообщений, при этом 2⁷-16=112 комбинаций не используются. Рассмотрим комбинацию 0111100, которая соответствует числу 12 в нашей таблице. Пусть при передаче символ на пятой позиции изменился (1 перешла в 0). Искаженная кодовая комбинация стала равной 0111000. Определим ошибку по изложенной выше методике. Из табл. 8-4 найдем позиции первой проверки 1, 3, 5, 7. Проверка дала нечетное число - ставим 1. Вторая проверка на позициях 2, 3, 6, 7 Дала четное число - ставим 01. Третья проверка дала четное число - ставим 1. В итоге проверочное число 101 =5. Следовательно, на 5-й позиции произошла ошибка. Знак на этой позиции необходимо изменить на обратный: 0→1.

Корректирующую способность кода можно повышать и дальше: строить коды для обнаружения r-кратной и исправления s-кратной ошибок. Конечно, при этом будет расти число дополнительных знаков и общая длина кодовой комбинации (при неизменном N=2^n₀). Обозначим через d наименьшее число знаков, которыми различаются между собой две кодовые комбинации. Очевидно, что

Возможности различных кодов видны из табл. 8-5.

Таблица 8-5