б) Геометрическая интерпретация корректирующих кодов

При построении корректирующих кодов часто прибегают к геометрической модели. Допустим, есть алфавит, состоящий уз трех символов. Из них можно составить следующие комбинации: 000, 001, 010, 011, 100, 101, 111. Возьмем три оси и будем откладывать точки с координатами, равными коду (рис. 8-5). Помеха может исказить сигнал, т. е. вместо 0 появится 1 или наоборот. Очевидно, что когда кодовые комбинации друг от друга отличаются на длину ребра d=1, то помеха переведет один сигнал в другой и обнаружить ошибку в этом случае нельзя. Ее можно обнаружить, если кодовые комбинации отстоят друг от друга на два ребра, т. е. 0, 011, 101, 110. Для исправления необходимо, чтобы комбинации отличались на три единицы: 000, 111.

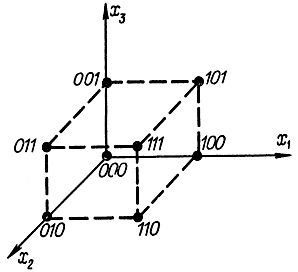
Рис. 8-5. Геометрическая интерпретация корректирующих кодов

Пространство, представленное на рис. 8-5, называется пространством Хэмминга, а величина d - расстоянием по Хэммингу. Очевидно, что это расстояние всегда целое число, равное числу разрядов, в которых отличаются двоичные числа, соответствующие точкам в пространстве Хэмминга. В более общем случае пространство Хэмминга имеет n координат и изображается n-мерным кубом.