в) Групповые коды

Набор кодов называется групповым кодом, если он составляет группу в точном математическом смысле [Л. 58]. Основное свойство группы заключается в замкнутости относительно некоторой заданной операции G. Это означает, что если к двум кодовым комбинациям или словам, принадлежащим группе, применить эту операцию, то получится слово, также принадлежащее этой группе, и сколько бы раз эта операция ни применялась к словам группы, она не дает слов, не принадлежащих к ней. Если операция G линейная, то код называется линейным или матричным.

Кроме свойства замкнутости для группы характерно свойство ассоциативности, которое для операции сложения записывается следующим образом;

В групповом коде всегда разрешается нулевой код или слово, состоящее из нулей.

Количество элементов в группе определяет порядок группы. Порядок может быть равен бесконечности. Операции сложения и умножения образуют группу с бесконечным порядком, состоящую из всех целых чисел и нуля. Мы ограничимся двоичными кодами, которые образуют группу по отношению операции сложения. Логические функции двух переменных образуют конечную группу. Если кодовое слово конечно, то группа разрешенных слов тоже конечна.

Групповые коды строят, исходя из количества информационных символов n₀ и минимального кодового расстояния по Хэммингу d_мин. В соответствии с требуемыми свойствами корректирующего группового кода выбирают d_мин минимальную общую длину кода n и число проверочных символов k согласно формуле (8-1). Однако часто ради простоты реализации алгоритмов идут на некоторую избыточность. Построим группу по отношению к операции сложения. Для этого выберем g ненулевых я-разрядных разрешенных кодовых слов и произведем сложение по два, по три и т. д. и, наконец, по g слов в соответствии с формулой

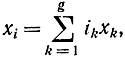
где x₁, x₂,..., x_k - исходные n-разрядные кодовые слова, состоящие из 0 или 1; i₁,i₂,...,i_g - коэффициенты, которые принимают значения 0 или 1. Суммирование в этой формуле осуществляется по модулю

2. Общее количество слов, получаемых с помощью этой формулы, равно:

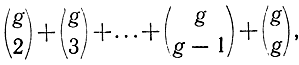
где

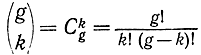
- число сочетаний из g по k. Если еще добавить g исходных слов, причем

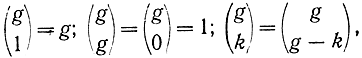
и 1 в счет нулевого слова, то получим:

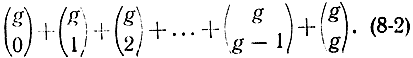
По исходным условиям код должен содержать

разрешенных кодовых слов. Для этого достаточно положить g=n₀, так как известно, что

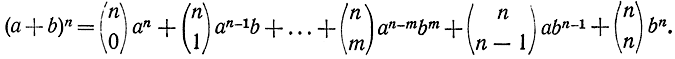
Положив в этой формуле а=b=1, получим:

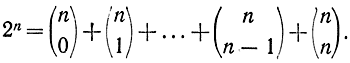
Естественно потребовать, чтобы все кодовые слова, количество которых определяется выражением (8-2), были оригинальными, т. е. отличались от нулевого слова и исходных g слов. Для этого необходимо, чтобы результат сложения по модулю два был равен нулю при равенстве между собою обоих слагаемых. Отсюда вытекает требование различности исходных слов. Нулевое слово не должно входить в состав исходных слов, так как при сложении с ним получается результат, совпадающий со слагаемым. Чтобы производные слова не совпали с исходными, должно выполняться условие

для любых c_i отличных от нуля. Это соотношение является условием линейной независимости кодовых слов x₁, x₂,..., x_n0 которые полностью определяют групповой код и называются базовыми словами или базой.

Для обеспечения заданного минимального кодового расстояния необходимо выполнение двух условий: каждое базовое слово должно содержать не менее d_мин единиц, и расстояние между любой парой базовых слов должно быть не меньше d_мин. Число единиц двоичного слова иногда называется весом слова v_i. Тогда первое условие может быть записано как

Второе условие для всех 1≤i≤n₀, 1≤j≤n₀ запишется в виде

Алгоритм построения базовых слов, обеспечивающих это условие при минимальной избыточности, на сегодняшний день не найден. Базовые слова принято записывать в виде матрицы

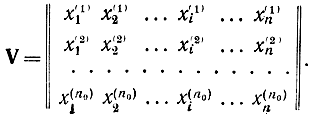
Эта матрица содержит n столбцов и n₀ строк и называется производящей матрицей кода (n, n₀).

Пример 8-3. Рассмотрим [Л. 58] случай с n₀=3 и d_мин=3. Очевидно, что следует выбрать k=3 в соответствии с формулой (8-1), чтобы n=n₀+k=6 тогда гарантируется d_мин=3. Образуем производящую матрицу

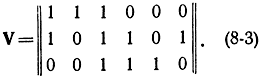
Нетрудно убедиться, что базовые слова удовлетворяют всем пяти необходимым условиям:

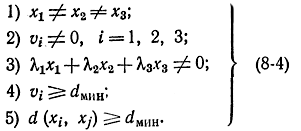
Первые три разрешенных слова совпадают с базовыми:

x₁=111000, x₂=101101, x₃=001110; четвертое слово - нулевое:

x₄=000000.

Остальные слова получаются суммированием базовых слов в различных сочетаниях:

Этот код обеспечивает d_мин=3, так как все ненулевые разрешенные слова имеют вес не менее d_мин. Однако если выбрать базовые слова 000111, 111000, 011110, удовлетворяющие всем пяти требованиям, то получим коды с d_мин=2. Действительно, сложив все три числа, получим 100001 с d_мин=2. Дело в том, что минимальное расстояние в подмножестве разрешенных слов равно минимальному весу:

так как в состав разрешенных слов входит нуль, и, кроме того, при сложении двух базовых слов x₁ и x₂ получается третье x₃ с единицами, стоящими на тех разрядах, в которых цифры не совпадают.

Так как операции сложения в групповых кодах осуществляются поразрядно, то можно произвольно перемещать столбцы производящей матрицы. При этом свойства кода (избыточность и корректирующие способности) не меняются, хотя разрешенные кодовые слова будут Другими. Поэтому всегда можно сосредоточить информационные символы в первых n₀ позициях, а проверочные - в последних n позициях. Эта возможность используется для записи производящей матрицы в каноническом виде. Такая матрица состоит из квадратной единичной матрицы ранга n₀, соответствующей не избыточному коду Длиной n₀. Она составляет левую под матрицу производящей матрицы. Справа от нее пишутся k столбцов проверочных символов.?

Таким образом, производящую матрицу для кода (n, n₀) можно записать в следующем каноническом виде:

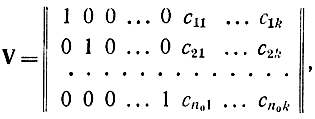
где c_ij - коэффициенты в линейной форме, с помощью которых из информационного символа получается контрольный, т. е.

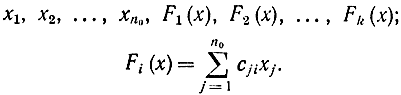
Нетрудно из производящей матрицы канонического вида получить проверочную или контрольную матрицу

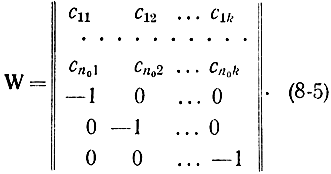
Корректирующий код (n, n₀, d) будет построен, если будет найдена соответствующая матрица ||c_ij||. Очевидно, если базисные кодовые слова выбраны правильно, то, представив производящую матрицу в каноническом виде, получим полное решение задачи.

Пример 8-4. Для кода, рассмотренного в примере 8-3, матрица для которого определяется формулой (8-3), получим:

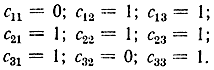
Нетрудно убедиться, что здесь правило составления корректирующих символов удовлетворяется:

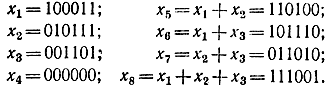
Для x₈ в первом корректирующем символе имеем: 0=1*0+1*1+1*1, во втором 0=1*1+1*1+1*0, в третьем 1=1*1+1*1+1*1. Напомним, что в соответствии с формулой

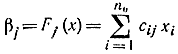
суммирование производится по первому индексу c_ij.

Рассмотрим с общих позиций построение групповых корректирующих двоичных кодов. Обозначим любое кодовое слово на входе линии

на выходе линии

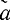₁,...,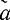_i,...,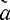_n0, β₁,...,β_i,...,β_k

где α_i - информационные, β_j - контрольные символы. Вектор шума представим в виде

Тогда

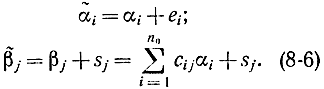
На приемном конце линии связи вычислим проверочные символы по информационным

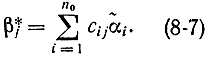
Нетрудно убедиться, что контрольное число (или синдром)

где y_j определяется в соответствии с формулой

Контрольное число z должно указывать позицию, на которой произошел сбой. Если подставить в равенство (8-8) соответствующие выражения (8-6) и (8-7) для β*_j и 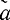_i, получим:

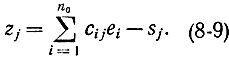
Отсюда следует, что синдром не зависит от комбинаций кода и определяется только вектором шума. Нетрудно убедиться, что все элементы синдрома равны нулю тогда и только тогда, когда принятая комбинация совпадает с одной из комбинаций кода. Действительно, если z_j=0, то из выражения (8-9) следует, что

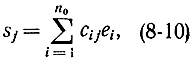
т. е. эта шумовая комбинация совпадает с одной из комбинаций кода, поэтому принятая комбинация принадлежит коду. Если в векторе помехи е только одна компонента e_i в информационной части отлична 0т нуля, то

Наконец, если ошибка происходит только в одном из контрольных разрядов, то

в частности, если элемент ошибки совпадает с обратным единице элементом s_j=-1, то

Обратные элементы необходимо вводить для ошибки даже в случае двоичного кода, чтобы получить формальный математический аппарат, причем условно считается, что в Группе кодов 1=-1.

Соотношение (8-11) указывает на то, что номер позиции контрольного числа, на которой располагается отличный от нуля элемент, совпадает с номером искаженного проверочного символа в случае, когда происходит однократная ошибка в контрольных символах. Отсюда не трудно получить правила составления элементов контрольной матрицы W [формула (8-5)1. Первые n₀ строк этой матрицы определяют контрольные числа, соответствующие изменению на +1 i-го информационного символа, а последние k строк определяют контрольные числа, соответствующие изменению на ту же величину j-го проверочного символа. Это при однократных ошибках. Так как для вычисления j-го элемента синдрома используются линейные операции, то контрольное число, которое соответствует многократным ошибкам, может быть найдено в виде линейной комбинации строк контрольной матрицы. Из матрицы W видно, что при умножении искаженного вектора х' на каждый ее столбец происходит проверка правильности линейной связи j-го контрольного символа со всеми информационными символами. Например, если произошел сбой на i-и позиции информационных символов и все c^ij(r = 1, 2, ..., k) отличны от нуля, т. е. эта позиция участвует во всех проверках, то во всех разрядах контрольного числа появится единица (при единичной ошибке). Действительно, можно доказать следующее положение. Если найдена линейная комбинация строк матрицы W, совпадающая с вычисленным контрольным числом, то номера этих строк совпадут с номерами искаженных позиций, а коэффициенты, с которыми они складывались, определят, как искажен символ на соответствующей позиции. Для исправления искаженных позиций необходимо найти элемент, противоположный каждому из указанных коэффициентов, и прибавить к соответствующему символу принятой комбинации. Очевидно, что одно и то же корректирующее число может быть получено в результате различных линейных комбинаций строк матрицы W. Поэтому в общем случае задача отыскания ошибки неоднозначна. Задача определения множества ошибок, которое корректируется данным кодом, в настоящее время не решена. Однако ясно, что множество шумовых комбинаций будет корректироваться данным кодом, если ошибкам, вызываемым в кодовой комбинации, будет соответствовать свое, отличное от нуля, контрольное число. Для этого шумовая комбинация е^r(r= 1, 2, ..., 2^k-1) не должна совпадать ни с одной из комбинаций данного кода, так же как и разность любых векторов е^r и e^s. Необходимость первого условия следует из доказательства, связанного с отношением (8-10).

Теперь докажем, что если разность двух векторов ошибок не образует комбинацию кода, то разным ошибкам, порождаемым разными шумовыми комбинациями, соответствуют разные синдромы. Пусть имеются два вектора шума

разность их

причем

Соответствующие синдромы, как следует из формулы (8-9), определяются соотношениями:

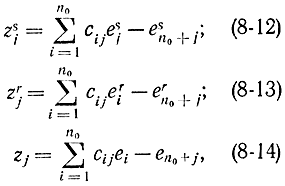
где j=1, 2,..., k. Из этих формул следует, что

поэтому синдромы (8-12) и (8-13) не будут совпадать, если среди элементов числа (8-15) хотя бы один отличен от нуля. Нетрудно убедиться, что правая часть соотношения (8-14) не обращается в нуль, так как по условию разность векторов ошибки не принадлежит коду. Отсюда можно утверждать, что каждое контрольное число может быть получено в результате 2^n₀ искажений символов кодовой комбинации. Действительно, если помехе e₁ соответствует некоторый синдром, тот же самый синдром соответствует помехе e₂, для которой

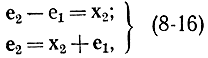
где х₂ - произвольная комбинация кода. Но, как уже указывалось, вектор х₂ (при фиксированном e₁) может принимать 2^n₀ комбинаций (контрольные символы определяются информационными). Таким образом, имеется 2^n₀-я неоднозначность, которую следует ликвидировать. Для этого с помощью соотношения (8-16) однозначно разбивают множество всех n-значных комбинаций на 2к непересекающихся подмножеств, каждому из которых соответствует свое контрольное число. Причем одно из этих подмножеств совпадает с кодовым словом и соответствует нулевому синдрому. Эти подмножества обладают всеми свойствами так называемых классов смежности. Из общей алгебры известно, что группу можно разбить на классы смежности, которые совпадают или не содержат ни одного общего элемента. В каждом смежном классе насчитывается 2^n₀ элементов, а всего классов, не считая класс, соответствующий нулевому коду, 2^k-1. Это значит, что 2^k-1 классов смежности или (2^n₀)^2k-1 кодовых комбинаций запрещено. Все это позволяет по-иному сформулировать ранее встречавшееся утверждение: множество шумовых комбинаций (имеется в виду искаженная шумом кодовая комбинация) корректируется данным кодом, если каждая из комбинаций принадлежит разным классам смежности. Процесс исправления ошибок происходит следующим образом. На приемном конце линии связи выписываются контрольные числа и соответствующие им искаженные комбинации (составляющие определенный класс смежности). При этом каждому синдрому ставится в соответствие только одна помеха. По принятому числу вычисляется контрольное число, которое с помощью специально составленных таблиц позволяет исправить код.

Пример 8-5. Рассмотрим [Л. 57] семизначный двоичный код

Составим код с d_мин=4. Отведем для контрольного числа четыре позиции, т. е. на одну больше, чем требуется для семизначного кода Хэмминга. Опять путем подбора и догадки выбираем базовую систему кодов в виде

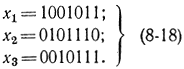
Нетрудно убедиться, что эта база удовлетворяет всем пяти условие (8-4). С помощью формул (8-17) получаем еще четыре кодовые комбинации, которые вместе с нулевым кодовым словом составляют нулевой класс смежности, состоящий из разрешенных кодовых комбинаций. Справа в соотношениях (8-18) стоит производящая матрица канонического вида. Поэтому подматрица, составленная из-четырех последних столбцов с добавлением единичной квадратной матрицы, составит контрольную матрицу, которая запишется в виде

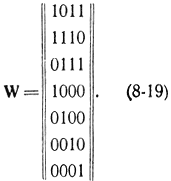
Первый класс смежности получается прибавлением к первой кодовой комбинации всех кодовых слов нулевого класса. Первая кодовая комбинация этого класса совпадает с кодом, помехи е=1000000 искажающей первый символ.

Второй класс смежности получается аналогичным образом с помощью помехи е=0100000 и соответствует контрольному числу, составленному из второй строки контрольной матрицы. Таким образом получаются все классы" до седьмого включительно. Классы смежности с восьмого по четырнадцатый соответствуют двукратной ошибке. Так, 11-й класс смежности соответствует ошибке е=0001100. Его контрольное число 1100 получается в результате сложения четвертой и пятой строк контрольной матрицы. Заметим, что то же самое контрольное число может быть получено в результате сложения первой и последней строк контрольной матрицы, что соответствует ошибке е = 1000001. Таким образом, в части обнаружения и исправления двукратных ошибок корректирующий код не является однозначным. 15-й класс смежности соответствует трехкратной ошибке вида е=0001101.

В результате получаем корректирующий код, исправляющий семь одиночных, семь двукратных и одну трехкратную ошибку, причем следует иметь в виду, что допускается любая одиночная ошибка, семь двукратных и только одна трехкратная.

Результаты построения кода сведены в табл. 8-6.

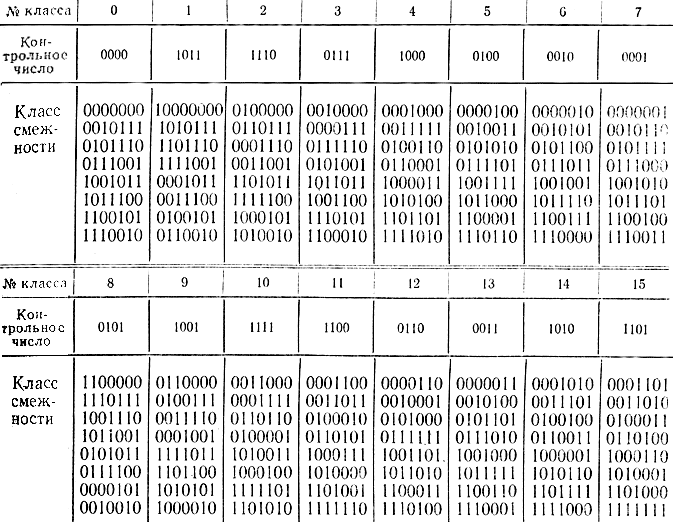
Таблица 8-6