10-2. О критериях оптимизации

Вопрос о критериях оптимизации - один из самых .важных в кибернетике, и в то же время он далек от удовлетворительного решения.

В последнее время- интенсивное развитие получила наука, называемая прагматикой, которая занимается определением целей и задач управления, изучением значения и ценности результатов поведения, движения, развития и управления системами. До последнего времени эта наука носила чисто качественный, не формализованный характер. Однако с развитием кибернетики появились первые попытки формализации методов прагматики с помощью семиотики и математической лингвистики. В качестве практической реализации кибернетических методов в этой области можно указать на американскую человеко- машинную систему "Паттерн",, предназначенную для научно-технического прогнозирования и определения оптимальных по значению и по времени реализации целей [Л. 15, 68J. Следует заметить, что, по-видимому, прагматика никогда не станет полностью формализованной наукой, так как с формализацией целей низшего уровня будут появляться новые цели целей на качественном уровне и такой процесс будет бесконечным. Тем не менее именно прагматика является той наукой, с помощью которой можно достаточно грамотно формулировать критерии управления.

В настоящее время выделяют два вида критериев оптимизации. Это, во-первых, выработанные практикой качественные или количественные характеристики оптимальности работы различных систем и, во-вторых, разработанные математиками математические критерии оптимальности, положенные в основу аналитических, графоаналитических, численных и машинных методов оптимизации. Однако они часто далеки от потребностей практики. В последнее время наблюдается сближение этих двух видов критериев: с одной стороны, появляются новые математические методы оптимизации, такие как принцип максимума и динамическое программирование, которые лучше приспособлены для решения практических задач оптимизации, с другой стороны, практика проектирования все чаще пользуется критериями оптимальности, удобными в математическом смысле. Так произошло с критерием среднеквадратичной ошибки, принятым в качестве оценки точности работы АСР, и критерием вероятности, утвердившимся как количественная оценка эффективности работы системы. Такой процесс стал возможным в связи с ростом математических знаний инженеров.

Критериев оптимизации в кибернетике много. Выбор того или иного критерия зависит от конструктура системы управления, и в этом содержится элемент нестрогости. Однако все чаще практика предлагает типовые критерии, которые становятся общепринятыми и заносятся в технические задания.

Наиболее распространенные в кибернетике методы оптимизации используют понятие минимума (или максимума) функции или функционала. В первом случае находят значение n переменных x₁,x₂,...,x_n, при которых функция F(x₁, x₂, ....,xⁿ) принимает экстремальное значение F=min (max). В простейшем случае дифференцируемости функции и неравенства нулю вторых производных задача сводится к решению n алгебраических (в общем случае нелинейных) уравнений

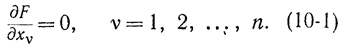
При оптимизации управления приходится оперировать с большим числом переменных (n=10³-10⁵). В этом специфика задач оптимизации, и это затрудняет решение уравнений (10-1) даже с помощью ЦВМ.

В качестве оптимизируемой функции могут выступать, например, величина дохода промышленного предприятия в рублях, количество энергии, потребляемой системой. Однако часто требуется определить закон управления в виде некоторой функции времени или других переменных. Если функция F(x), где х={х₁, х₂,...,x_n} помимо переменных x₁,x₂,...,x_n зависит еще (параметрически) от другой переменной λ (или переменных λ₁, λ₂,...,λ_n) то решение для каждого значения λ соотношения (10-1) дает оптимальный закон управления

Здесь мы уже переходим, по существу, к понятию функционала, частным случаем которого является функция. Методы оптимизации, использующие этот критерий, возникли задолго до кибернетики и составили содержание раздела математики, названного вариационным исчислением. Понятие функционала в математике является дальнейшим обобщением понятия функции. Не очень строго функционал можно определить как функцию от функции, т. е. функцию, в которой в качестве независимой переменной выступает функция. Это определение ошибочно относят к функционалам функции вида F[φ(x)], [x²]³ и т. д., которые, однако, являясь функциями, представляют частный случай функционала.

Если одному множеству М значений величины х(х∈М) соответствует другое множество N значений величины y, то говорят, что у является функцией х, т. е. y=f(х). Например, М {1, 4, 9, 8} и N {20, 70, 90, 110}. Каждому значению из множества М соответствует одно значение из множества N. Это - метод задания функции в виде таблиц. Он чаще всего встречается в кибернетике. Аналитически функция может быть задана в виде y=x³, y=sin х.

Если М - множество функций и каждой функции f(х), принадлежащей М {f (х)∈ М}, ставится в соответствие определенное значение величины у из множества N, то говорят, что на множестве М задан функционал. Например,

и

Другим примером функционала может служить определенный интеграл

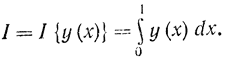
Каждой функции y(х) будет соответствовать числовое значение I. Так, при y=хI=1/2, при y=x²I=1/3. Можно поставить задачу отыскания такой функции y(х), которая обращала бы этот функционал в минимум (максимум), т. е.

В общем случае подынтегральное выражение в функционале может зависеть явно от аргумента х, y и производной yx:

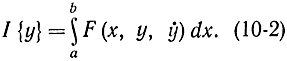
Интеграл в формуле (10-2) может пониматься в смысле Лебега - Стильтьеса или интеграла от обобщенной функции (в частности, содержащей дельта-функции). Тогда нетрудно показать, что запись (10-2) включает в себя функцию. Так, если положить

то

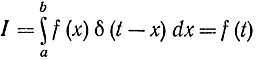
при a<t<b.

Аналогично, если положить

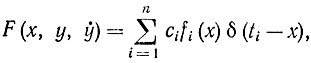
то

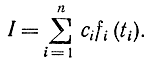
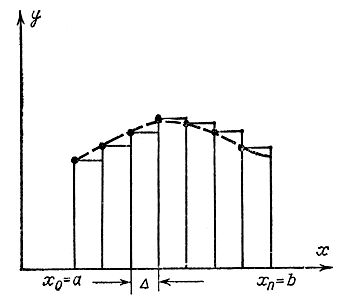
Рис. 10-1. К замене функционала суммой

Иногда считают, что функционал является функцией бесконечного числа переменных. Соответственно вариационное исчисление можно рассматривать как обобщение методов отыскания экстремума функции на случай большого или бесконечного числа переменных. Действительно, функцию y(х) в формуле (10-2) можно заменить приближенно ломаной линией (рис. 10-1) с вершинами y₀=y(х₀)=y(а), y₁=y(x₀+Δx),...,y_n=y(x₀+nΔx)=y(b), а функционал - суммой

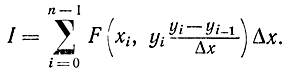
После этого вариационная задача приближенно решается как обычная задача на отыскание экстремума функции n переменных: I=(y₁,y₂,...,y_n). Именно так выводил свое основное уравнение вариационного исчисления Эйлер [Л. 69, 70].

Особое место в методах оптимизации занимает критерий оптимизации с ограничениями. В случае функционала этот критерий может?

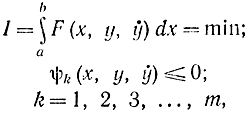
где ψ_k- некоторые функции. Смысл этих соотношений состоит в том, что отыскивается не любая функция y(х), обращающая функционал в минимум, а такая, которая удовлетворяет системе ограничений. Нетрудно убедиться, что тем самым значение условного экстремума не может быть меньше значения абсолютного экстремума (без ограничений). Аналогичным образом формулируется критерий оптимальности (с ограничениями) для функции

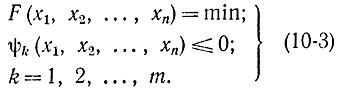
В классическом вариационном исчислении в функционале интеграл понимается в обычном смысле как предел сумм Дарбу, а не как интеграл Лебега -Стильтьеса [Л. 69]. В целях соблюдения инженерного уровня изложения здесь будет использовано это классическое понятие функционала (если не дано специальных оговорок).

Следует заметить, что во всех приведенных формулах переменные х и y могут быть векторами

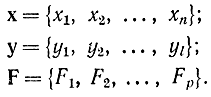
Такая форма записи широко используется, и, в частности, она учитывает случаи оптимизации функции многих переменных и оптимизации нескольких функций.

Задачи оптимизации при наличии ограничений, по существу, привели к пересмотру классических методов и созданию новых методов, известных под названием методов программирования. Если в формулах (10-3) все функции линейные, налицо задача линейного программирования. В общем случае эти соотношения определяют задачу нелинейного программирования.