15-2. Пассивный поиск

Не во всех ситуациях можно реализовать последовательную про- Цедуру поиска. Так, при управлении доменным или химическим процессом, когда нет времени на последовательный анализ, делается одновременный параллельный замер параметров. При этом возникает необходимость определения новых значений управляющих параметров, которые обеспечили бы оптимальную близость к экстремуму.

Или, например, группа из десяти экономистов должна решить задачу оптимального распределения ресурсов в условиях ограниченного заказчиком времени (одна неделя). Такое условие заставляет построить работу по параллельной схеме, т. е. каждый экономист ведет поиск в отдельности по заданной ему программе распределения ресурсов. Если бы заказчик не торопил с решением вопроса и выделил вместо одной недели четыре, то десять экономистов могли бы совместно последовательным поиском рассчитать четыре варианта и получить ту же точность, что и при пассивном поиске при расчете десяти вариантов. Если бы в их распоряжении было десять недель, то совместная работа по последовательной схеме дала бы эффективность в 18 раз большую, чем при пассивном поиске (см. табл. 15-1). В этой модели условно считалось, что при совместной работе десяти экономистов по последовательной схеме время расчёта одного варианта остается равным неделе. Однако можно составить другую модель, предположив, что при совместной работе время расчета одного варианта сокращается в 10 раз. Тогда уже к концу второго дня получился бы тот же самый результат, что и при пассивном поиске к концу недели (считается, что рабочих дней в неделе пять).

Для случая двух экспериментов пассивная стратегия ничем не отличается от активной, так как информацию, полученную от одного эксперимента, нельзя использовать для уточнения второго эксперимента. Пусть имеются результаты двух экспериментов (N=2): x¹, х², причем 0≤х¹<х²≤1. С помощью соотношений (15-1) - (15-3) можно написать:

На рис. 15-4 показаны кривые L²=const в зависимости от х¹=х₁ и х²=х₂. Из-за условия x¹>x² оптимальное на первый взгляд значение L²=0,5 при х¹=х²-0,5 отвергается. Поэтому вводится минимальная величина ε, которая определяется погрешностью измерительной аппаратуры, позволяющей при различии между х¹ и х², равном ε, обнаружить разницу между соответствующими y¹ и y². Тогда в результате экспериментов х¹ =0,5-ε/2 и х²-0,5+ε/2 можно получить не только требуемое разделение y¹ и y², но и минимально возможное значение L²_опт

Только что рассмотренная стратегия носит наименование ε-минимаксной.

Теперь рассмотрим случай трех экспериментов и постараемся улучшить довольно плохой план, ранее рассмотренный и представленный на рис. 15-3 (х¹=0,2; х²; x²=0,6; х³=0,9). Ранее было получено максимальное значение интервала неопределенности, равное 0,7. Из рис. 15-3, б видно, что можно уменьшить L³, сблизив х¹ и х³, в связи с чем, уменьшив х³ и увеличив х¹ на 0,1, получим (рис. 15-5):

При этом

Теперь, перемещая х² влево, можно еще уменьшить L³, однако одновременно будет увеличиваться х⁴-х²=1-х². Поэтому для выбора х² следует рассмотреть график функции

в интервале 0,3=х¹<х²<x³= ,8. В соответствии с рис. 15-6 минимальное значение функции (15-4) получается при х₂=х²=0,5. Это значение и выбирается в оптимальной минимаксной стратегии. Таким образом, оптимальной стратегией будет всякая пассивная стратегия (х¹, х², х³), для которой х²=0,5 (рис. 15-7, а) и х³-х

≤0,5 (рис. 15-7, б) и которая дает оптимальное значение L³_опт= 0,5.

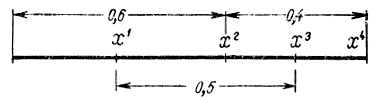
Рис. 15.5. Улучшенный вариант пассивного поиска при трех экспериментах

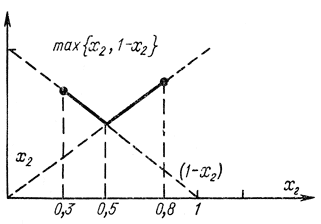
Рис. 15-6. К определению эффективности пассивного поиска при трех эксперементах

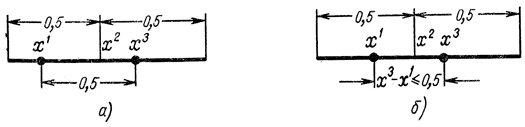
Рис. 15-7. Оптимальные пассивные стратегии при трех экспериментах

Определение минимаксной стратегии с помощью рис. 15-7 практически совпадает с геометрическим методом отыскания оптимальной стратегии в теории игр [Л. 35].

Из рассмотренных двух примеров следует, что добавление третьего эксперимента, требующего дополнительных средств и усилий, в случае пассивного поиска мало себя оправдывает, так как разность L³_опт-L²_опт составляет малую величину ε/2. Оказывается, что это положение остается справедливым [Л. 92] для любого числа опытов N, т. е. использование нечетного числа опытов целесообразно только при большой погрешности измерений ε, поэтому часто на практике используют поиск парами экспериментов. Можно показать, что наилучший выбор получается при разделении экспериментальных точек на равноотстоящие пары. При таком распределении процедура носит название поиска однородными парами. Так, при n=2 (рис. 15-8, а) эксперимент состоит из двух значений: 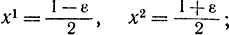при n=4 (рис. 15-8, б) — из четырех значений:

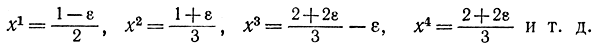
Аналитически значения x^k при поиске однородными парами можно задать с помощью формулы

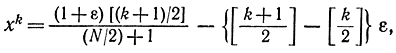
где квадратные скобки [а] обозначают наибольшее целое число, не превышающее а[π]=3, [4]= 4 и т. д.

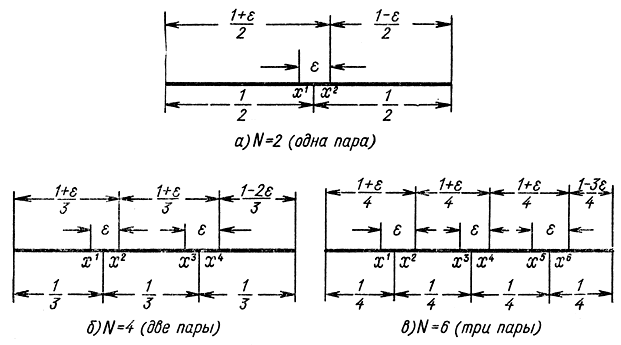
Рис. 15-8. Поиск однородными парами

Из предыдущего следует, что такая схема для четного числа опытов представляет ε-минимаксную стратегию, так как смещение любого из экспериментов только увеличивает L^N. Величина оптимального интервала неопределенности задается формулой.

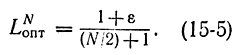
Нетрудно показать [Л. 92], что для числа опытов N+1

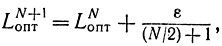
где N - четное, т. е. с увеличением числа опытов разница между оптимальными интервалами неопределенности при четном и нечетном числе опытов уменьшается примерно обратно пропорционально числу опытов.