15-1. Особенности одномерного поиска

Рассмотрим три случая с тремя экспериментами (рис. 15-3). Значения x в каждом эксперименте отстоят от левого конца исходного интервала неопределенности [0,1] соответственно на величины х¹=0,2; x²=0,6; x³=0,9. Каждая из трех позиций рисунка содержит три возможных результата экспериментов. В каждом из трех случаев максимальное значение достигается соответственно в первом (рис. 15-3,а), втором (рис. 15-3, б) и третьем (рис. 15-3, в) экспериментах. Обозначим через К номер эксперимента, в котором получен наилучший в смысле максимума результат:

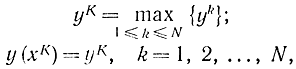
где N - число экспериментов. Для каждого из трех случаев можно указать новый, более узкий интервал неопределенности, в котором лежит оптимальное значение х. Действительно, при К=1 0≤х_опт<x²; при К=2 х¹<х_опт<х³; при К=3 x²<x_опт≤1

Можно получить общую формулу для экспериментов, если обозначить через х⁰ начало исходного интервала неопределенности, т. е. х⁰=0, и через x^N+1 его конец x^N+1=1 Тогда для интервала неопределенности l^N после

причем

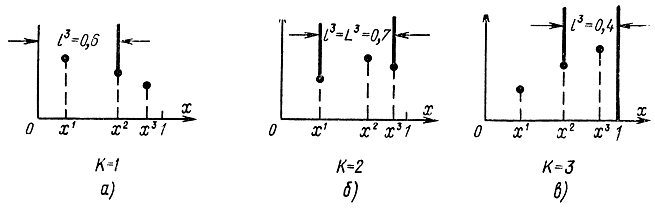
Рис. 15-3. К определению меры эффективности поиска при трех экспериментах

В зависимости от стратегии поиска (выбора x^k) получаются разные значения интервалов x^k+1-х^k-1(k=1, ..., N). Из результатов эксперимента (значений y^k) видно, при каком k=К получается наилучший результат y^k и соответственно наилучшее значение интервала неопределенности lⁿ. Таким образом, l^N определяется, с одной стороны, распределением x^k и, с другой стороны, номером К:

Эта величина является хорошей мерой эффективности поиска после завершения всей серии из N экспериментов. Но нам нужна априорная мера эффективности, a l^N до серии экспериментов неизвестна. Поэтому введем в рассмотрение наибольший из l^N (т. е. наихудший) интервал неопределенности

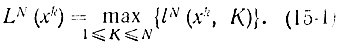
Нетрудно убедиться, что L^N зависит только от стратегии поиска (выбора x^k), и, конечно, от унимодальной зависимости y(x) и не зависит от интервала, в котором окажется значение x_опт, т. е. величины К. Для нашего примера имеем:

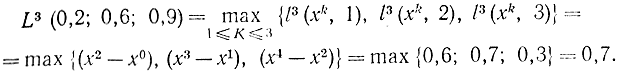
Величина L^N - единственная при заданной стратегии поиска (выборе x^k), так как среди возможных значений l^N только одно или, в крайнем случае, несколько равных между собой значений будут наибольшими. Выбор в качестве меры величины lN для наихудшего случая избавляет нас от нежелательной зависимости от результатов испытаний и дает априорную, хотя и пессимистическую оценку эффективности поиска. При реальном поиске может получиться лучший результат.

После того как введена мера эффективности поиска, можно указать критерий выбора оптимального поиска, в качестве которого берется минимум величин:

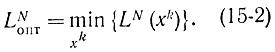
Оптимальная стратегия х^k_опт определяется соотношением

Величина L^N_опт - постоянная и единственная для данной унимодальной зависимости. Она определяет минимальный интервал неопределенности, хотя оптимальных стратегий х^k_опт может быть несколько. Стратегия х^k_опт может быть названа минимаксной, так как

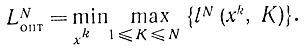
Нетрудно убедиться, что

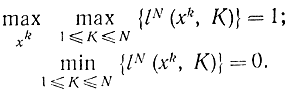
По существу, изложенный выше метод определения оптимальных стратегий характерен для теории игр. В данном случае ведется игра против природы.