б) Метод Фибоначчи

В современной интерпретации этот метод был предложен Кифером, хотя корни его восходят к математику XIII века Фибоначчи и даже к более ранним исследованиям Евклида.

Будем считать, что для исследования исходного интервала неопределенности единичной длины было выделено N экспериментов, N - 1 из которых выполнены. В последнем эксперименте требуется исследовать интервал неопределенности L^N-1_опт держащий точку-эксперимент Е₊^N-1 для которой получено самое большое значение y при первых N - 1 испытаниях (рис. 15-10). Положение точки E₊^N-1 целиком зависит от стратегии поиска. Последнюю точку E^N можно выбрать произвольно, но не ближе, чем на расстоянии ε от точки E^N-1. Ситуация на этом последнем шаге полностью совпадает с обычным поиском при наличии двух экспериментов. Минимальное значение последнего интервала L^N_опт получается, если точки Е^N-1₊ и E^N расположить симметрично на расстоянии ε/2 относительно середины интервала L^N-1_опт. Поэтому значения L^N-1_опт и L^N_опт связаны соотношением

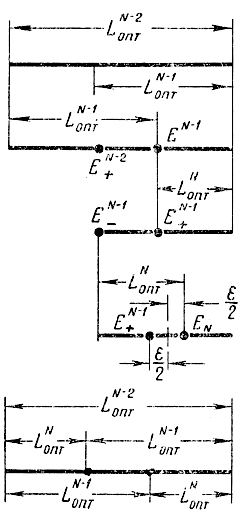
Рис. 15-10. Пояснение к методу Фибоначчи

Продолжая процедуру движения с конца, аналогичную динамическому программированию, введем в рассмотрение интервал неопределенности L^N-2_опт, который получается в результате N-2 экспериментов из общего числа N. Внутри этого интервала содержится эксперимент Е₊^N-1 дающий наибольшее значение y при первых N-2 экспериментах. В этом интервале следует произвести следующую пару экспериментов. Лучшее значение из двух обозначим через Е^N-1₊. Другая точка из этой пары, которую обозначим через Е^N-1_-, будет граничной между частью L_опт^N-2 интервала L_опт^N, исключаемой и частью L^N-2_опт, оставляемой для рассмотрения. Но в начале эксперимента неизвестно, какое из двух значений E^N-1 будет наибольшим и обозначится как Е^N-1₊ а какое наименьшим и обозначится как Эти два значения могут меняться местами. Поэтому обе точки Е^N-1₊ и Е_N-1- располагаются на одинаковом расстоянии L^N-1_опт от концов интервала. Так как эти точки расположены симметрично относительно середины интервала L_опт^N-2 и одна из них становится E^N-1₊ (причем это может быть любая из двух точек E^N-1), то каждая из них должна находиться на расстоянии L^N_опт от одного конца интервала и на расстоянии L^N-1_опт от другого конца интервала. При этом учитывается, что ранее была доказана формула (15-6). Поэтому

С учетом формулы (15-6) напишем:

Аналогично можно доказать для любого 1<k<N, что

Отсюда при k=N-2

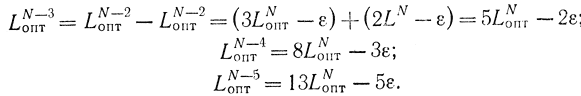
Для удобства записи формул введем последовательность чисел Фибоначчи:

в соответствии с которой имеем:

С помощью этих чисел можно записать следующую формулу для оптимальных интервалов неопределенности:

Полагая длину исходного интервала равной единице, получаем:

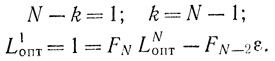
Отсюда находим оптимальный интервал после N опытов:

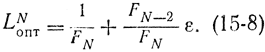
Как видно из приведенной позднее табл. 15-1, для уменьшения интервала неопределенности более чем в 100 раз по методу Фибоначчи необходимо провести 11 опытов, по методу дихотомии- 14, а при пассивном методе - 198 [см. формулу (15-5)]. При методе Фибоначчи каждая последующая точка выбирается симметрично по отношению к точке, которая осталась от предыдущего эксперимента и попала в оставшийся интервал. Первый эксперимент следует выбирать на расстоянии L²_опт от одного из концов начального интервала, безразлично от левого или правого, в силу симметрии. Чтобы получить точное выражение для L²_опт воспользуемся формулой (15-7), учитывая, что N-k=2 и k=N-2:

Исключив из этого соотношения L^N_опт, с помощью ^формулы (15-8) получим:

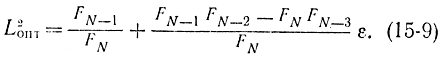
Используя тождества F_N-1=F_N-2+F_N-3, F_N=F_N-1+F_N-2 которые следуют из самого определения чисел Фибоначчи, напишем:

Можно доказать [Л. 92], что правая часть этого равенства равна (-1)ⁿ, поэтому формулу (15-9) можно переписать в виде

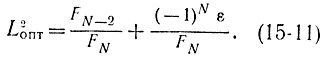
Формула (15-11) позволяет начать процедуру поиска, если известны ε и N. В этом состоит недостаток метода: требуется заранее знать необходимое число опытов. Очень часто задается только величина интервала неопределенности, которую надо знать к концу N-го опыта. Эта особенность придает последовательному методу Фибоначчи свойства пассивного поиска. Она напоминает взаимоотношения классической процедуры Неймана - Пирсона и последовательного метода Вальда в теории проверки статистических гипотез (см. гл. 3). Иногда поэтому обращаются к методу дихотомии, который хотя и обладает меньшей эффективностью по сравнению с методом Фибоначчи, но не требует предварительного знания числа опытов.

Однако существует другой метод поиска, который почти также эффективен, как метод Фибоначчи, но не требует априорного задания числа опытов N. Имеется в виду известный издавна метод золотого сечения.