в) Метод золотого сечения

Итак, необходимо избавиться от зависимости первого опыта от числа опытов. Для этого поступаем следующим образом. По-прежнему считаем, что сохраняется условие симметричности последовательных экспериментов, так же как в методе Фибоначчи, т. е. справедливо соотношение

Однако вместо условия

при котором в методе Фибоначчи интервал L²_опт зависит от N, предлагается условие

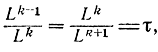
означающее постоянство отношения длин последовательных отрезков. Отсюда следует, что

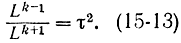
Учитывая соотношение (15-13) и поделив обе части (15-12) на L^k+1, получим:

Положительный корень этого квадратного уравнения

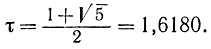
По результатам двух экспериментов выбирают часть исходного отрезка, внутри которого расположен один из предыдущих опытов. В следующую пару опытов включают эту точку, а вторую выбирают внутри остающегося отрезка симметрично точке, оставшейся от предыдущего опыта. Первые точки найдутся на расстоянии 1/τ от левого и правого концов единичного начального интервала. Процесс можно продолжать как угодно долго. После N опытов интервал неопределенности достигнет

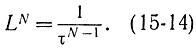
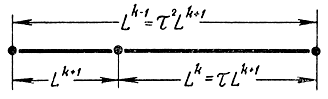
Рис. 15-11. Пояснение к методу золотого сечения

Рассмотренная процедура носит название метода золотого сечения.

Она состоит в делении отрезка на две неравные части так, чтобы отношение всего отрезка к большей части равнялось отношению большей части отрезка к меньшей (рис. 15-11). Математик Люкас вывел уравнение, связывающее числа Фибоначчи F_N и величину τ:

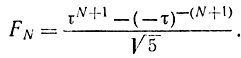
При больших N вторым членом в формуле Люкаса можно пренебречь, в результате чего получим:

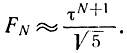
Это соотношение дает возможность получить связь интервалов неопределенности L^N после N опытов при методе золотого сечения и при методе Фибоначчи:

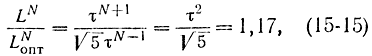
т. е. эффективность метода золотого сечения только на 17% ниже метода Фибоначчи. При больших N, как это следует из уравнения Люкаса, имеем

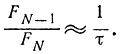
Отсюда с учетом формул (15-10) и (15-14) для больших N

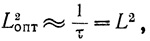
т. е. при больших N обе процедуры начинают поиск в одних и тех же точках.

В табл. 15-1 приведены цифры, характеризующие уменьшение исходного единичного интервала неопределенности для различных методов поиска.

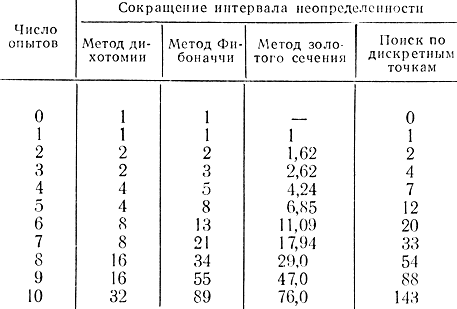
Таблица 15-1