15-10. Методы отыскания экстремума в условиях помех
Быстрая сходимость при наличии помех может привести к асимптотической ошибке, т. е. поиск будет сходиться к неправильному значению. Основным ограничением в скорости уменьшения интервала поиска является уровень шумов [Л. 92].
Допустим, требуется найти нуль хопт функции y(х), измерение значений которой z(х) производится с ошибками. Сделаем ограничения относительно помехи. Будем считать, что y(х) - несмещенная оценка функции г (х), т. е.
М{z(х)}=y(х).
Очевидно, что y(х) является функцией регрессии для случайного процесса z(х).
Далее предположим,. что дисперсия ошибки есть величина ограниченная, т. е.
σ2z(x)=М {[z(х)-y(x)]}<∞ (15-23)
В процедуре Робинсона - Монро х изменяется по закону
хk+1=хk-γkz(xk),
где xk и xk+1 - значения x в k-м и (k + 1)-м экспериментах; z(xk) - результат измерения на k-м шаге.
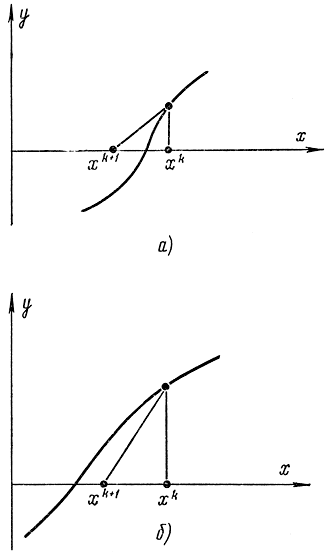
Рис. 15-25. Пояснение к методу поиска нуля функции
Смысл стохастической аппроксимации очень прост: на каждом шаге коррекцию вносят пропорционально значению функции, измеренному на предыдущем шаге. Допустим что помеха отсутствует или мала (рис. 15-25). Тогда в зависимости от вида функции и значения коэффициента yk возможны два случая: в результате коррекции точка xk+1 или не дойдет до нуля функции y(x) (рис. 15-25, б), или перейдет за него (рис. 15-25, а). В первом случае процесс поиска монотонно сходится к нулевой точке, во втором случае он носит колебательный характер. При наличии помех процесс носит тот же характер. Коэффициенты yk определяют тангенс угла, образованного гипотенузой треугольников с вертикальной прямой (рис. 15-25, б):
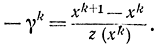
В методе стохастической аппроксимации γk задаются заранее и должны удовлетворять определенным условиям. Во-первых, для сходимости процесса поиска необходимо, чтобы
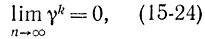
во-вторых, последовательность величин γk не должна сходиться, т. е.
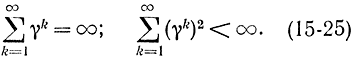
В этом смысле в качестве γk можно выбирать гармоническую последовательность:
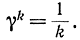
Не вдаваясь в сложные математические выкладки, условие (15-25) можно объяснить следующим образом. Если длина шага уменьшается в соответствии со сходящимся рядом, то процесс может не дойти до нуля, так как величина общей коррекции ограничена. Очевидно, что ряд
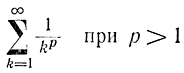
сходится, т. е.
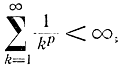
а при p<1 расходится, т. е.
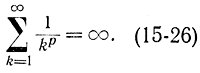
Однако ряд, составленный из квадратов коэффициентов, должен сходиться:
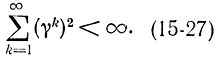
Этому условию опять удовлетворяет гармоническая последовательность
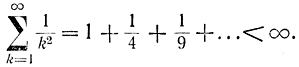
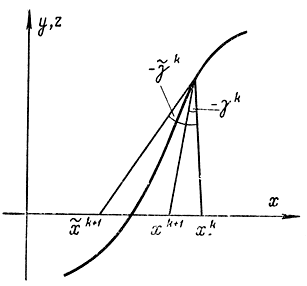
Рис. 15-26. Геометрический смысл коэффициента γ
Смысл этого условия заключается в том, что случайная составляющая о должна уменьшаться с ростом k.
В силу изложенного чаще всего в качестве последовательности коэффициентов коррекции выбирается гармоническая последовательность.
Наконец, имеется еще одно условие, которому должно удовлетворять множество значений x и z(х). Так как коррекция на каждом шаге
пропорциональна значению z(х) на предыдущем шаге, то надо быть уверенным, что величины z(xk) ограничены. Выше было наложено ограничение на величину дисперсии ошибки y(х)-z(х), поэтому достаточно потребовать, чтобы была ограничена функция регрессии (рис. 15-27):
|y|<А|х-хопт|+В<∞ (15-28)
Величины A и В должны быть конечны, но не обязательно известны. Если величина А известна хотя бы приближенно, то можно ускорить поиск. Робинсон и Монро доказали, что при условиях (15-23) - (15-27) эта процедура сходится в среднеквадратичном смысле, т. е.
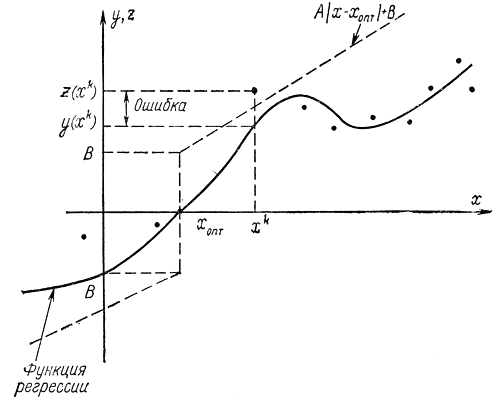
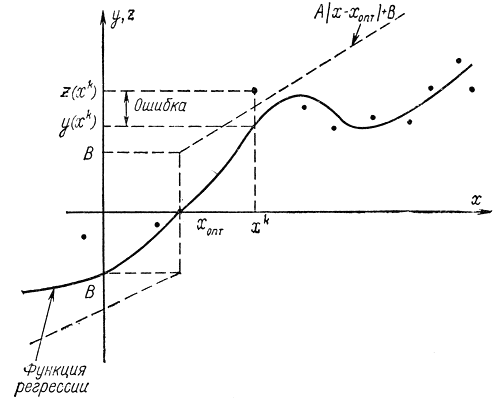
Рис. 15-27. Пояснение к методу Робинсона - Монро
Блюм доказал, что эта процедура сходится с единичной вероятностью:
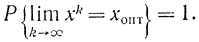
Мы не будем заниматься доказательством сходимости, с этим можно познакомиться в книге Уайльда [Л. 92], где обе эти теоремы следуют из более общей теоремы Дворецкого. Укажем, что в многомерном случае, когда х и функции y и z представляют собой векторы
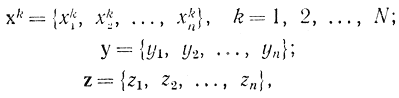
процедура Робинсона - Монро при аналогичных условиях обеспечивает сходимость к нулю хопт вектор-функции y(х). В этом случае процедура запишется в виде
xk+1=xk-γkz(x)
или
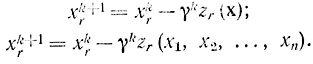
Однако при многомерном варианте остается неясным выбор последовательности координат r= 1, 2,.., n, по которым следует делать шаги. В конце параграфа будут приведены некоторые конкретные варианты выбора последовательности.
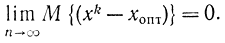
Рис. 15-28. Пояснение к методу Кифера - Вольфовица
При отыскании максимума функции для одномерного случая в условиях помех следует написать формулу для метода Робинсона - Монро применительно к производной y(х), обозначив ее измерение через z(х). Тогда получим:
xk+1=xk + γkz(xk),
т. е. процедура стохастической аппроксимации в этом случае изменяет шаг пропорционально производной от функции на k-м шаге или пропорционально градиенту в многомерном случае. Таким образом, это просто градиентный метод. Но в результате дифференцирования функция z(хk) гораздо сильнее загрязнена шумами [больше отличается от y(хk), чем z(х) от y(х)]. Кифер и Вольфовиц предложили не дифференцировать функцию, а изменять шаг пропорционально величине
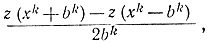
где bk - некоторая постоянная. Очевидно, что при малом bk эта величина пропорциональна производной z (рис. 15-28). Поэтому процедура Кифера - Вольфовица для одномерной задачи задается формулой
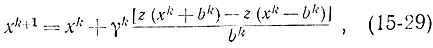
где γk - положительные числа. Коэффициенты должны удовлетворять условиям
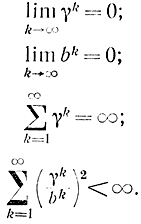
Для сходимости необходимо выполнение не очень жестких ограничений. В том числе требуется, чтобы значения среднего углового коэффициента функции регрессии y(х) для любой пары наблюденных точек лежали в пределах некоторого сектора, ограниченного прямыми линиями:
|y(x2)-y(x1)|<A|x2-xопт|+B<∞
где хопт - истинная координата вершины; x1≠x2. Это условие аналогично условию (15-34) в случае процедуры Робинсона - Монро.
Имеются также условия, аналогичные несмещенности оценки и ограниченности дисперсии помехи. При этом доказано, что процедура сходится (т. е. процесс сходится к точке максимума) как в среднеквадратичном, так и в вероятностном смысле при условии одного максимума (унимодальной функции).
Еще раз напоминаем, что как метод Робинсона -Монро, так и метод Кифера - Вольфовица по существу являются градиентными методами отыскания экстремума.
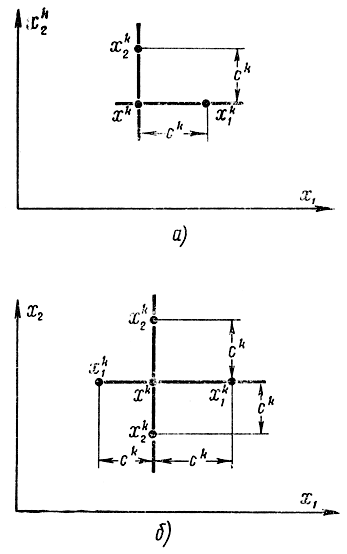
Рис. Пояснения к многомерному поиску а - метод Блюма; б - метод Сакса
Если производная (или градиент) велика в данной точке (например, крутая гора), необходим большой шаг, так как k-я точка находится далеко от экстремума (вершины). При малой производной шаг в соответствии с формулой (15-29) становится меньше, чтобы не "проскочить" экстремум (вершину). Для многомерного случая идеи методов Робинсона - Монро и Кифера - Вольфовица реализуются в методах Блюма и Сакса.
При многомерном поиске по методу Блюма (рис. 15-29, а) очередной наклон касательной в точке xk определяется по замерам в этой и других точках, отличающихся от xk тем, что к каждой координате добавляется величина ck. Если обозначить через ej - единичный вектор с j-й координатой, равной единице, и всеми остальными координатами, равными нулю, то аналитически испытуемые точки запишутся в виде
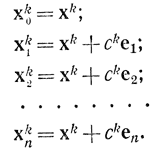
В качестве градиента в методе Блюма используется вектор с компонентами
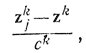
где zkj=z(xkj) - величина замера в точке xkj, которая из-за ошибок отличается от истинного ykj. Сама процедура поиска запишется как
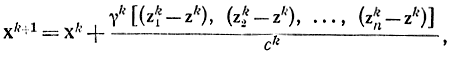
где γk - текущая длина шага. Для сходимости величины ук и ск должны удовлетворять тем же условиям, что и в одномерном методе Кифера - Вольфовица.
Однако, как показал Сакс, из-за асимметричности точек возможно их группирование около ложного положения экстремума, что замедляет поиск. Поэтому Сакс предложил симметричную процедуру поиска, требующую двух экспериментов по каждой координате. В соответствии с рис. 15-29, б к точкам xki необходимо добавить еще n точек:
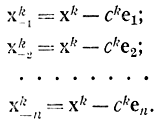
Так как в точке xkn эксперимента не производится, то метод Сакса требует 2n точек по сравнению с n + 1 точками в методе Блюма. Тогда процедура симметричного поиска запишется в виде
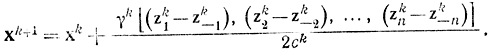
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'