15-9. Овражный метод

Если топография поверхности имеет овражный характер (рис. 15-23), то градиентный метод становится малоэффективным, так как движение будет происходить последовательно с одного склона на другой с очень медленным продвижением к точке минимума x_опт.

В связи с этим разработано много эвристических методов ускоренного продвижения вдоль оврага или гребня, которые так или иначе основаны на релаксационном методе, являющемся обобщением рас-смотренных методов. В общем случае релаксационный итерационный метод основан на следующей формуле:

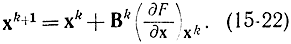
Один метод отличается от другого выбором матрицы B^k.

Так, градиентный метод получается, если B^k=λЕ, где Е - единичная матрица. Метод по координатного спуска может быть получен из формулы (15-22), если в матрице B^k все элементы, кроме одного, расположенного на диагонали, равны нулю. На каждой итерации положение ненулевого элемента выбирается заново.

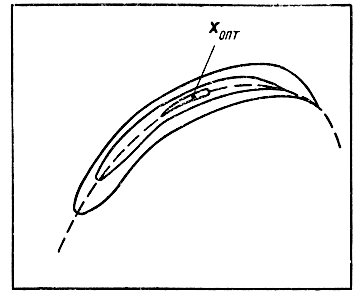
Рис. 15-23. Линии уровнений при наличии оврагов

При первом овражном методе [Л. 93] задается малое положительное число ε₁. В очередной точке x^k вычислим все производные dF/dx_j. Далее осуществим градиентный спуск, полагая равными нулю производные, абсолютное значение которых меньше ε_i т. е.

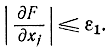
Этот метод обеспечивает быстрый спуск на дно оврага. Для ускоренного движения по дну оврага вводят другое большое положительное число ε₂>>1. Опять используют метод градиентов, но полагая равными нулю все те производные, для которых

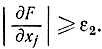
Другой метод ускоренного движения по оврагу заключается в следующем. Вначале выбирают две близкие точки x⁰ из них градиентным методом спускаются с малым шагом в точки х₁ соответственно. Далее через них проводят прямую и вдоль нее делают большой овражный шаг λ в точку х₂, где процесс повторяется и определяется новое направление овражного шага (рис. 15-24).

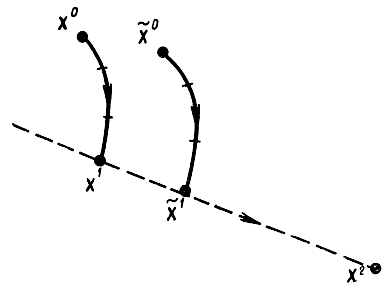
15-24. Метод оврагов