16-6. Прямая и двойственная задачи линейного программирования

а) Предварительные сведения

Прямая задача линейного программирования ставится следующим образом. Находят значения переменных (x₁, x₂,...,x_n), удовлетворяющие условиям:

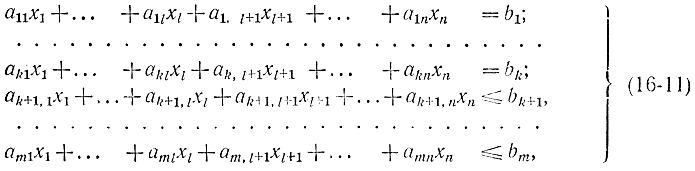
обращающим в максимум линейную форму

При этом допускается, что часть переменных x₁,...,x_l имеет любые знаки, а переменные x_l+1,...,x_n≥ 0.

Прямой задаче соответствует двойственная, в которой определяются двойственные переменные, удовлетворяющие соотношениям:

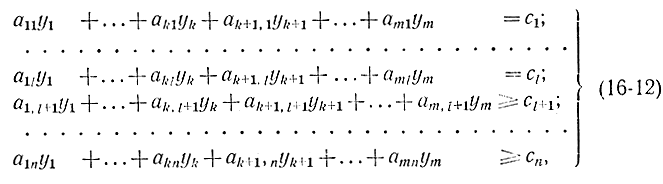
обращающим в минимум линейную форму

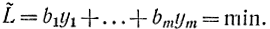
Здесь переменные y₁, ...,y_k также могут иметь произвольные знаки, y_k+1,...,y_m≥0. Заметим, что l равенствам (16-12) соответствуют свободные переменные x₁,...,x_n а n - l неравенствам - неотрицательные переменные прямой задачи x_l+1,...,x_n. И наоборот, k равенствам прямой задачи (16-11) соответствуют свободные (неограниченные по знаку) переменные y₁,...,y_k неравенствам - неотрицательные переменные y_k+1,...,y_n двойственной задачи.

Коэффициенты b_j стоящие в правой части ограничений прямой задачи, фигурируют как коэффициенты линейной формы в двойственной задаче, а коэффициенты линейной формы прямой задачи становятся коэффициентами правых частей ограничений двойственной задачи. Матрица А^т коэффициентов левых частей ограничений двойственной задачи является транспонированной матрицей А коэффициентов левых частей прямой задачи. Запишем эти матрицы в виде:

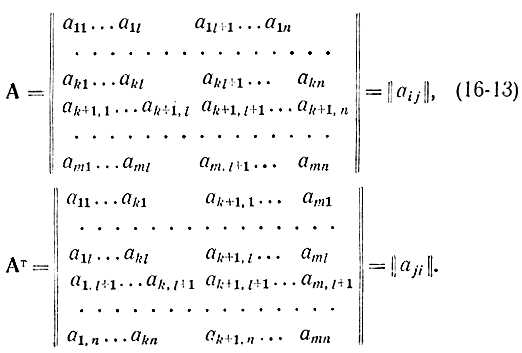
В предлагаемом руководстве в основном, если нет специальных оговорок, используется матрица прямой задачи с m строками и n столбцами и i меняется от 1 до m, а j - от 1 до n. Поэтому переменные и коэффициенты имеют соответственно индексы x_j, a_ij, y_i, b_i, c_i. Соответственно число ограничений двойственной задачи равно числу неизвестных n прямой, а число неизвестных двойственной задачи равно числу ограничений m прямой задачи.

Кроме того, можно доказать так называемую теорему двойственности, которая утверждает, что

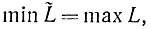
т. е. оптимальные значения функционалов для решений прямой и двойственной задач совпадают.

Все высказанные положения о взаимоотношении прямой и двойственной задач строго доказываются в специальных руководствах. Однако сейчас можно заметить, что все эти свойства основаны на свойстве замкнутости пары прямой и двойственной задач, которое заключается в том, что задача, двойственная к двойственной, совпадаете основной, иногда они называются взаимно двойственными. По существу, используя метод конструирования, мы специально так подобрали формализм прямой и двойственной задачи, чтобы удовлетворить сформулированному выше свойству замкнутости. Если попробовать изменить, к примеру, что-нибудь в формулировке двойственной задачи (минимум заменить на максимум или число свободных переменных изменить с k на k + 1), то это приведет к тому, что задача, двойственная к двойственной, не совпадет с прямой. На определенном уровне строгости, принятом в методе конструирования, никаких других доказательств не требуется. Свойство замкнутости (двойственности) широко используется и по существу является укрупненным свойством, с помощью которого можно экономным способом доказывать различные положения и получать методы оптимизации.

Программа накрутки голосов в конкурсах.