б) Некоторые свойства взаимно двойственных задач

Рассмотрим две системы линейных однородных уравнений:

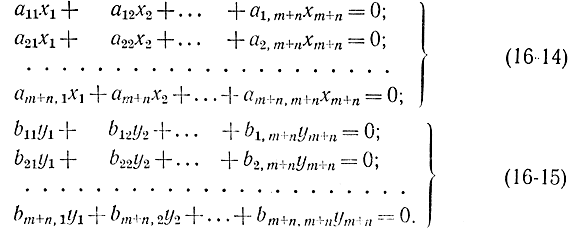
Первая система содержит m + n переменных, из которых m переменных x_i1, x_i2,...,x_in базисные и n переменных x_j1, x_j2,...,x_jn не базисные (свободные), причем набор чисел i₁, i₂,...,i_m; j₁, j₂,..,j_n представляет собой некоторую перестановку из чисел 1, 2, m + n. Базисные переменные выделяются в системе (16-14) свойством независимости векторов

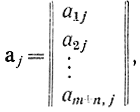
составленных из коэффициентов при базисных переменных. Как правило, считается, что на базисные переменные наложено условие не отрицательности. Кроме того, для удобства в дальнейшем будем часто считать, что базисными переменными являются m первых переменных x₁, x₂,...,x_m, чего всегда можно достигнуть изменением нумерации переменных и коэффициентов в исходной системе. Не базисные (свободные) переменные не ограничены по знаку.

Аналогично вторая система содержит n базисных y_k1, y_k2,...,y_kn и m не базисных y_l1, y_l2,...,y_lm переменных, где набор индексов k₁, k₂,...,k_n; l₁, l₂, ..., l_m также представляет собой перестановку чисел 1, 2,...,m + n. Благодаря независимости векторов a_j и b_k составленных из соответствующих коэффициентов при базисных переменных, детерминанты квадратных матриц, составленных из этих векторов с учетом только их элементов, соответствующих независимым уравнениям с номерами базисных переменных, будут отличны от нуля:

Поэтому можно базисные переменные выразить через не базисные и переписать соотношения (16-14) и (16-15) следующим образом:

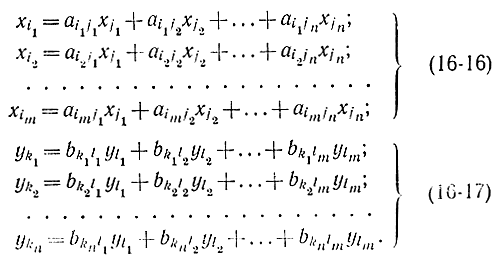
Если подсчитать коэффициенты систем (16-16) и (16-17) условиям

что для систем (16-14) и (16-15) соответствует

то пары систем (16-16), (16-17) и (16-14), (16-15) станут взаимно двойственными однородными линейными системами. Соотношение (16-18) имеет принципиальное значение, так как оно устанавливает жесткую связь двух наборов переменных в виде

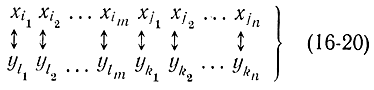
т. e. базисным переменным одной системы соответствуют не базисные переменные другой системы. Заметим, что если вместо (16-18) использовать условия

то связь переменных (16-20) преобразуется к виду

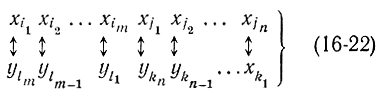
Еще раз заметим, что, имея в виду соответствующее изменение нумерации исходных уравнений и переменных, всегда можно считать, что базисными переменными являются первые m переменных m и последние n переменных y.

Аналогично различие между соотношениями (16-18) и (16-21), так же как и между (16-20) и (16-22), непринципиально и носит условный характер.

Условия (16-18) и (16-21) означают, что матрицы коэффициентов исходных уравнений являются транспонированными одна по отношению к другой и отличаются знаком, что использовалось ранее при определении прямой и двойственной задач линейного программирования.

Можно доказать, что если в одной из двух взаимно двойственных задач перейти к новому базису, а в другой к соответствующему базису, то взаимная двойственность систем сохранится. Это является основой так называемого двойственного симплекс-метода (или метода улучшения оценок) решения задач линейного программирования. Доказательство построим по методу полной индукции. Обозначим через число базисных переменных, подлежащих замене. Рассмотрим вначале вариант с p = 1, считая что из базиса удаляется переменная x_i1, а вводится x_j1. Для этого необходимо, чтобы a_i1j1≠0, так как в противном случае детерминант матрицы коэффициентов при новых базисных переменных не будет отличен от нуля. В двойственной системе эта замена повлечет соответствующую замену вида y_k1→y_l1 Такая замена базиса возможна, так как b_k1l1=-a_i1j1. Чтобы получить запись системы (16-16) в новом базисе, необходимо из первого уравнения выразить x_j1 и подставить это значение в другие уравнения. В результате получим:

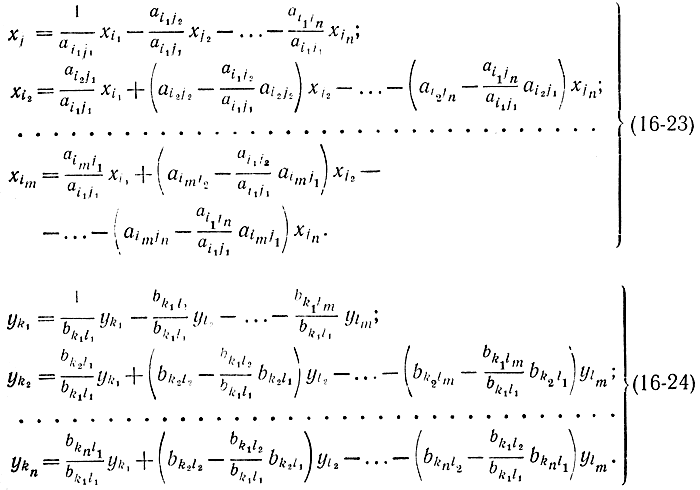
Нетрудно убедиться, что системы (16-23) и (16-24) являются взаимно двойственными. Действительно, коэффициент при x_j2 в выражении для x_l2 со знаком минус равен коэффициенту при y_l2 в выражении для y_k2 т. е.

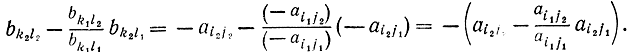
Тем самым сохранение взаимной двойственности систем при р — 1 доказано. Теперь, предполагая, что оно справедливо для р — 1, докажем его для случая, когда число заменяемых переменных равно р. Будем считать, что из базиса удаляются переменные x_i1, x_i2,...,x_ip и вводятся переменные x_i1, x_i2,...,x_ip. Чтобы такая замена стала возможной, детерминант

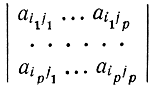
должен быть отличен от нуля. Для этого необходимо, чтобы хотя бы один из миноров порядка этого детерминанта был отличен от нуля. Допустим, что отличен от нуля минор

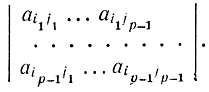
Это обеспечивает возможность такой замены, при которой переменные x_j1, x_j2,...,x_jp-1 становятся базисными, а переменные x_i1,...,x_ip-1 не базисными если после этой замены сделать x_jp базисной переменной вместо x_ip, то получается исходная замена р переменных. Тем самым показано, что замену можно производить в два этапа: вначале заменить р - 1 переменных затем одну переменную. И так как для р - 1 сохранение взаимной двойственности систем при замене переменных справедливо по исходному предположению, а выше была доказана его справедливость при замене одной переменной, то отсюда следует, что оно справедливо в силу индукции для любого р.