16-8. Выбор исходного допустимого решения
Допустим, задача линейного программирования записана в виде
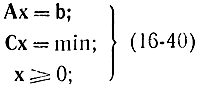
где b≥0; C=||c1, c2, ...,cn||. Исходный базис считается найденным, если ограничения, содержащиеся в задаче (16-40), записаны так
xv=bv-(av,mxm+1+...+aavnxn), v=1,2,...,m
где bv≥0, так как положив не базисные переменные xm+k = 0 (k = 1, 2, ..., n - m), получим значения xv = bv≥0, которые являются допустимыми и соответствуют одной из вершин.
Иногда сразу удается выделить первый базис. Однако в общем случае это не простая задача.
Для каждого ограничения вводим вспомогательную переменную zi ( i = 1, ..., m). Тогда ограничения системы (16-40) будут выглядеть как
Ax + z = b; х≥0; z≥0. (16-41)
Без нарушения общности считаем, что b неотрицательна, так как этого всегда можно достигнуть, поменяв соответствующие знаки в строках матрицы А. Поэтому допустимым базисным решением будет х = 0, z = b. Соответствующая симплекс-таблица на первом шаге запишется в виде
z = b - Ах,
т. е. за базис взят вектор z.
На первом шаге минимизируется функция цели 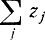 при ограничениях (16-41). Непосредственно из этих ограничений следует, что если минимум функции Σzj является положительной величиной, то система (16-41) не имеет неотрицательных решений, для которых x1,...,zm =0, так как в противном случае minΣzj = 0. Это означает, что исходная система (16-41) не имеет неотрицательных решений. Если minΣzj =0, т. е. zj = 0 для всех j, то вектор z является базисным. Отправляясь от этого базиса, мы стремимся прийти к базису, не содержащему ни одной вспомогательной переменной
при ограничениях (16-41). Непосредственно из этих ограничений следует, что если минимум функции Σzj является положительной величиной, то система (16-41) не имеет неотрицательных решений, для которых x1,...,zm =0, так как в противном случае minΣzj = 0. Это означает, что исходная система (16-41) не имеет неотрицательных решений. Если minΣzj =0, т. е. zj = 0 для всех j, то вектор z является базисным. Отправляясь от этого базиса, мы стремимся прийти к базису, не содержащему ни одной вспомогательной переменной
xv=bv-(av,m+1xm+1+...+avnxn+av1z1+...+avmxm), v=1,2,...,m(16-42)
где bv≥0. Полагая в системе (16-41) zj = 0, придем к системе
xv=bv-(av,m+1xm+1+...+avnxn) v=1,2,...,m
которая равносильна исходной (16-40). Но здесь x1, x2,...,xm - базисные переменные. Следовательно, задача нахождения базиса решена. Может получиться, что при переходе от базиса z1, z2,...,xm к следующему эти переменные будут оставаться в следующем базисе. Тогда необходимо постепенно их перевести в не базисные.
Если среди неизвестных x1, x2,...,xmимеется такая переменная, например x1 которая входит только в одно уравнение, например в первое, причем коэффициент при этой переменной a11 имеет тот же знак, что и свободный член b1 тогда не имеет смысла вводить для первого уравнения искусственную переменную, так как x1 сразу войдет в базис. Действительно, первое уравнение можно представить в виде
x1=b'-(a'12x2+...+a'1nxn)
где b1 = b1/a11≥0. Если таких неизвестных несколько, то все их можно сразу включить в базис.
Пример 16-4. Дана система
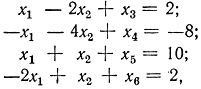
рассмотренная в примере 16-2. Так как x3, x5, x6 входят каждая только в одно ограничение и коэффициенты при них имеют тот же знак, что и соответствующие свободные члены, включаем их сразу в базис. Для оставшегося ограничения вводим искусственную переменную z1. В итоге получаем:
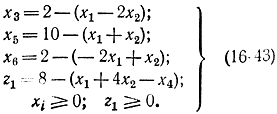
С помощью симплекс-метода требуется минимизировать форму L1=z1=8-(x1+4x2-x4) при ограничениях (16-43). Составляем симплекс-таблицу на первом шаге (табл. 16-6).
Симплекс-таблица

Таблица 16-6
Необходимо минимизировать L. Опорный элемент выбираем на пересечении строки х3 и столбца x1 После первого шага получаем базис (x1, x5, x6, z1). На втором шаге опорный элемент выбирается на пересечении строки z1 и столбца х4, поэтому искусственная переменная z1 выводится из базиса. При этом L1 = 0. Таким образом, базис найден и состоит из х1, х2, х5, х6:
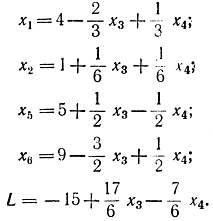
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'