16-7. Общая теория симплекс-метода с позиции линейной алгебры

Рассмотрим задачу линейного программирования

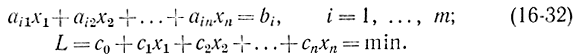
Будем считать, что система уравнений (16-32) содержит r линейно независимых уравнений, где r≤m. Эти r переменных на первом шаге являются базисными переменными, т. е. определяют базис. Строго говоря, с практической точки зрения можно считать, что r=m, так как в противном случае равенства (16-32) иди не совместны, или хотя бы одно из них представляет линейную комбинацию остальных и поэтому является лишним. Разрешив уравнения (16-32) относительно

этих переменных, получим:

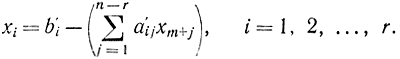
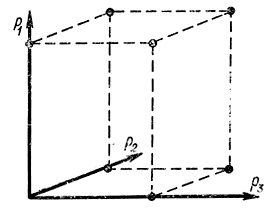
Рис. 16-8. Геометрическая интерпретация базисных переменных для третьего случая

Без потери общности можно считать, что независимы первые r уравнений (16-32). Предположим, что b'_i свободные коэффициенты неотрицательны. Каждое из этих уравнений можно рассматривать как проекцию векторного уравнения

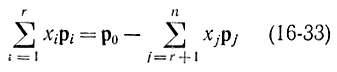
на единичные векторы, направленные по координатным осям (ортам) p₁, p₂,..,p_r где

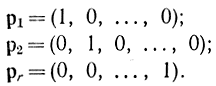
Векторы p₁,...,p_r образуют базис в m-мерном пространстве (рис. 16-8). При этом матрица разложений векторов p₀, p₁, p₂,..,p_n в базисе p₁, p₂,..,p_r представляется в виде

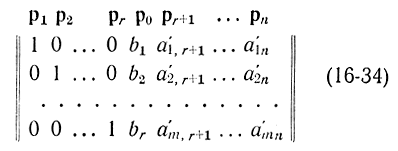
В этой матрице первые r столбцов представляют собой орты системы координат. Столбец r + 1 состоит из свободных членов ограничений. Последние n - r столбцов состоят из компонент проекций вектор-столбцов p_r+1,...,p_n на орты p₁, p₂,..., p_r. В целом матрица состоит из n + 1 вектор-столбцов с m компонентами каждый.

Очевидно, что симплекс-таблица теперь примет вид табл. 16-5.

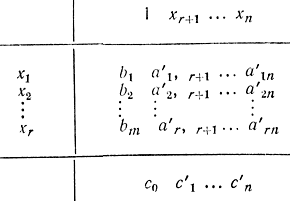
Таблица 16-5

Причем соотношением для L как

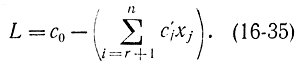
Следующей не базисной переменной, которую следует включить в базис, будет такая x_j (j= r+1,..., n), в столбце которой имеется положительная c'_j. Пусть это будет столбец j₁

Исключается из базиса та переменная x_i (i = 1, ..., r), для которой выражение {b_i/a'_ij1} минимально для всех положительных a'_ij1. Пусть это будет переменная i₁. Тогда новый базис будет состоять из координат x_j1 и x_i (i = 1, ..., i₁ - 1, i₁ + 1). которые выражаются через не базисные переменные следующим образом:

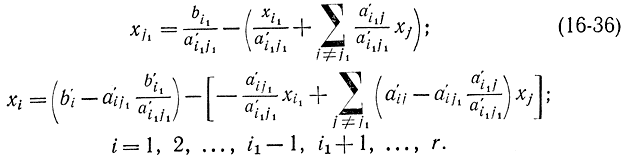
Эти формулы прямо следуют из формул (16-33).

Группа векторов p₁, p₂,..,p_i1-1, p_i1-1, p_j1, p_i1+1,...,p_r образует новый базис, так как их определитель, записанный в старой системе координат, отличен от нуля. Действительно,

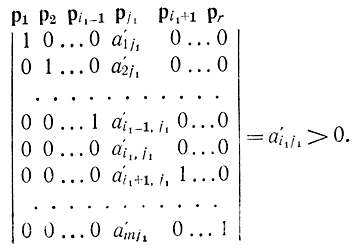
Следовательно, эти векторы независимы и могут быть выбраны за новый базис. В данном случае этот базис не нормирован, но если разрешить переменную x_j1 как это сделано в соотношении (16-36), то на втором шаге снова придем к матрице вида (16-34).

Повторяя этот процесс до тех пор, пока все числа в последней строке симплекс-таблицы (16-5) станут не положительны, получим оптимальное решение. Еще раз напомним, что в практически важных случаях r=m.

В зависимости от конкретных значений коэффициентов симплекс-таблицы 16-5 могут представиться три взаимоисключающие возможности:

1. с₀ и с'_j≥ 0 для всех j. В этом случае базисное решение будет оптимальным, так как всякое увеличение любой из независимых переменных (которые не могут стать отрицательными) в силу не отрицательности коэффициентов c_j привело бы к увеличению, а не к уменьшению значения линейной формы L.
2. c_j<0 по крайней мере для одного j=j₁ и a'_hj1≥0 для всех h. В этом случае значение линейной формы можно сколько угодно уменьшать. Увеличив до сих пор равную нулю переменную x_r+j1 и оставив за другими независимыми (не базисными) переменными их прежнее нулевое значение, получим, что функция L в силу условия c_j1<0 будет монотонно уменьшаться. Базисные переменные не уменьшаются, так как a'_hj10. Здесь имеет место "оптимальный луч", определенный соотношениями
   
   
   на котором линейная форма не ограничена снизу:
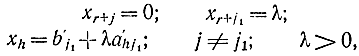   L=c₀+λc_j1→-∞
3. c_j<0 по крайней мере для одного j=j₁, и для всякого такого h имеется по крайней мере одно i = i₁ такое, что a_i1j1<0. В этом случае, делая замену переменных, можно прийти к новому базису с меньшим значением L. Увеличивая независимую переменную xr+jiy будем уменьшать L, но в отличие от второго случая здесь будут уменьшаться и такие зависимые переменные, для которых a_i1j1<0. Переменную x_r+j1 можно увеличивать лишь до тех пор, пока какая-нибудь до сих пор положительная базисная переменная не обратится в нуль. Будем считать, что эта переменная одна и имеет номер i₁. Очевидно, что критерием выбора этой переменной может служить
   
   

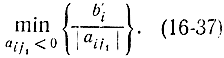
В результате получаем новый базис, в который вместо переменной x_i1 введена x_r+j1. Если имеется несколько переменных, для которых выражение (16-37) принимает одинаковые значения, например x_l1 и x_l2 то эти переменные одновременно обращаются в нуль. Включив x_i1 базис, видим, что x_i2 также примет нулевое решение, хотя она и остается базисной. Здесь имеет место вырожденный случай, так как функция L неоднозначно определяется значениями независимых переменных. Так, если b'_i1=0 и ai_i1j1<0, то нельзя увеличивать xr+jl, так как xit примет отрицательное значение. Поэтому xr+Il хотя и входит в базис, но сохраняет нулевое значение, другие переменные и L тоже сохраняют постоянное значение, т. е. выполнено "холостое" симплекс-преобразование, которое может привести к зацикливанию, приводящему к бесконечному процессу счета. Однако имеются формальные правила, позволяющие обойти зацикливание.

Мы уже имели дело с другой, расширенной по сравнению с табл. 16-5 симплекс-таблицей, которая содержит n + 1 столбец, т. е. в нее по примеру матрицы (16-34) включены в соответствии с векторным уравнением (16-33) еще r столбцов, соответствующих базисным переменным, причем каждый из этих столбцов содержит только один ненулевой элемент, равный единице. Если сокращенная таблица соответствует векторному равенству

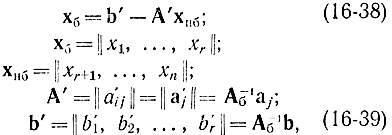
где А_б - подматрица А, состоящая из независимых столбцов a_j=||a_ij|| то расширенная симплекс-таблица соответствует равенству