17-4. Выпуклое программирование
Интенсивное развитие нелинейного программирования в значительной степени вызвано доказанной в 1951 г. фундаментальной теоремой Куна и Таккера о седловой точке в задачах выпуклого программирования. Эта теорема распространяет результаты о минимаксе, полученные в предыдущем параграфе применительно к классическому варианту для задач на условный экстремум, на случай задания ограничений в виде неравенств. Особый интерес представляет эта теорема для не дифференцируемых функций, о чем вообще не говорилось в классических методах.
Вначале получим условия существования седловой точки у непрерывной функции двух векторных переменных. Затем покажем, что эти условия удовлетворяются для оптимальной точки задачи нелинейного программирования.
Условия существования седловой точки. По определению функция Φ (х, λ) двух векторных переменных х = || x1,...,xn || и λ = || λ1,...,λn|| имеет в точке (хопт, λопт) седловую точку, если выполняются соотношения
Φ (х, λопт) ≤ Φ (хопт, λопт) ≤ Φ (хопт, λ) (17-19)
для всех х и λ из ε-окрестности (хопт, λопт). Будем считать, что х≥0 и λ≥0. Геометрически соотношение (17-19) интерпретируется с помощью рис. 17-8 и 17-9. При этом допускается и вырожденный случай, когда в левой или правой части стоит знак равенства.
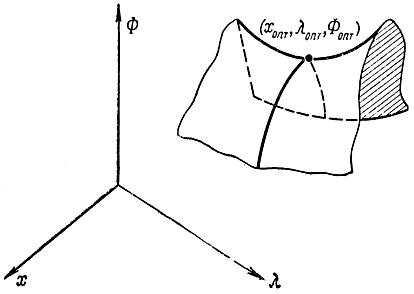
Рис. 17-8. Седловая точка
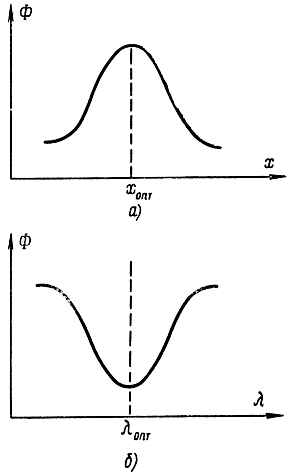
Рис. 17-9. Пояснение к седловой точке функции двух переменных
Докажем, что необходимыми и достаточными условиями существования седловой точки для функции двух векторных переменных являются соотношения
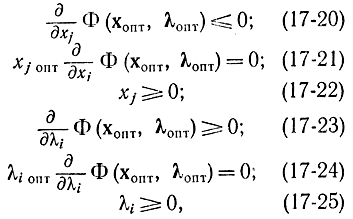
т. е. требуется доказать, что из условий (17-19) следуют (17-20) - (17-25) (необходимость) и из условий (17-20) - (17-25) следуют (17-19) (достаточность). Действительно, если при xj≥0 предположить соотношения, обратные (17-20) и (17-21), т. е.
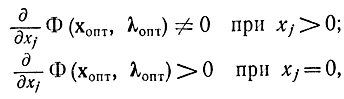
то это означало бы, что точка хопт при λ = λопт не является максимумом, так как для внутренних точек, где xj > 0, в точке максимума должна равняться нулю первая производная
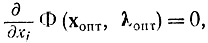
а на границе области, где xj = 0, первая производная для случая максимума должна быть не положительна, т. е.
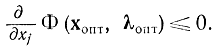
При этом подразумевается, что для внутренних точек, где xj>0, соотношение (17-20) носит характер строгого равенства, а для граничных точек, где xj = 0, - характер неравенства. Соотношение (17-21) выполняется для внутренних точек за счет равенства нулю производной, а для граничных точек - за счет равенства нулю координаты. Аналогично доказывается необходимость условий (17-23) и (17-24) при 0, т. е. они следуют из условия минимизации функции Φ (х, λ) относительно λ, если учесть, что при фиксированном х эта функция линейная относительно λi.
Действительно, если учесть, что
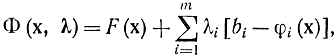
то соотношение (17-23) является просто другой записью исходных ограничений
φi(x)≤bi
так как
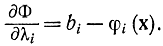
Как было показано ранее [формулы (17-17) и (17-18)], если в окрестности точки экстремума bi - φi(х)≥0 и в точке экстремума bi - φi(хопт) > 0, то соответствующие λiопт = 0. Для тех индексов i, при которых в точке экстремума (и малой окрестности ее) bi - φi(х) = 0, Φ (х, λ) = F (х), λiопт ≠0 (а именно λi>0). Поэтому всегда или λi= 0, или dΦ/dλi = 0 и соотношение (17-18) выполняется.
Другой способ доказательства справедливости соотношений (17-23) и (17-24) аналогичен использованному ранее доказательству справедливости соотношений (17-21) и (17-22). А именно, так как функция Φ (х, λ) при фиксированном хопт имеет минимум по λ, в точке λ = λопт, то для внутренних точек λ > 0 dΦ/dλi = 0, а для граничных λ = 0 dΦ/dλi ≥ 0.
Тем самым доказано, что из условий существования седловой точки (17-19) следуют соотношения (17-20) - (17-25). Чтобы доказать их достаточность для существования седловой точки, предположим вогнутость функции Φ (х, λ) по х и, разложив ее в ряд Тейлора, получим:
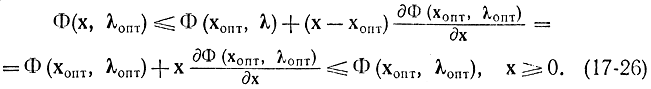
В формуле (17-26) под производной dΦ(x,λ)/dx, понимается градиент функции Φ по х, т. е.
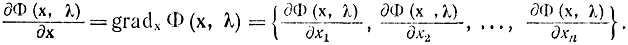
Очевидно, что для вогнутой функции в соответствии с рис. 17-10 значение ординаты, касательной вблизи точки вогнутости (хопт, λопт), не менее значения самой функции. Кроме того, если сложить все равенства (17-21) по j, получим:
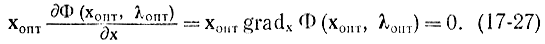
В соответствии с этой формулой в соотношении (17-26) справедлив знак равенства.
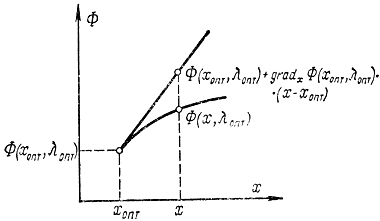
Рис. 17-10. Пояснение к разложению вогнутой функции в ряд Тейлора
И, наконец, если сложить по j все соотношения (17-20), получим:
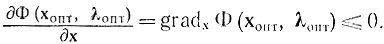
Поэтому в соотношении (17-36) при х≥0 справедлив последний знак неравенства. Тем самым доказана левая часть соотношения (17-19), т. е. условие максимума функции ФΦ(х, λ) по х в точке (хопт, λопт). Доказательство правой части этой формулы может выполняться двумя путями. Для любой выпуклой по к функции Φ (х, λ) аналогично соотношению (17-27) можно написать:
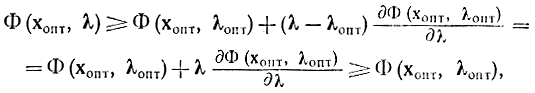
или, учитывая линейность Φ (х, λ) по λ,
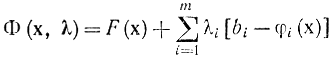
(и не предполагая выпуклости ее по λ), получаем:
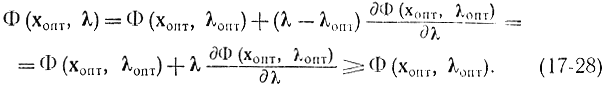
Первый знак равенства справедлив в силу линейности функции Φ (хопт, λ) относительно λ. Второй знак равенства справедлив или в силу соотношений (17-24), если их просуммировать по i, или в силу уже применявшихся рассуждений о том, что или dΦ(х, λ)/dλi = 0, или λiопт = 0. Тем самым доказана правая часть соотношения (17-19) и достаточность условий (17-20)-(17-25) для существования седловой точки.
Если имеется в виду седловая точка с минимумом по х и максимумом по λ, то соотношения (17-19) - (17-25) перепишутся в виде
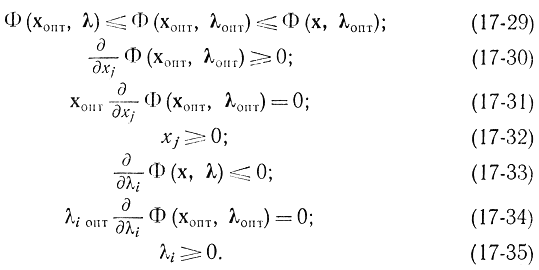
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'