в) Минимаксная трактовка задачи на условный экстремум функции

Предположим, что функция F (х) имеет в точке х_опт максимум при ограничивающих условиях φ_i (х) = b_i (i = 1,..., m). Соответствующий этой точке множитель Лагранжа обозначим через λ_опт = ||λ_1опт,...,λ_mопт ||. Если исключить особые случаи, то можно считать, что функция Лагранжа Φ (х, λ_опт) имеет в точке х_опт безусловный максимум, т. е.

для всех х из некоторой малой ε-окрестности точки х_опт. Опять, исключая из рассмотрения особые случаи, считаем, что для некоторой окрестности δ точки λ_опт функция Φ (x, λ) имеет безусловный максимум по х и удовлетворяет условиям

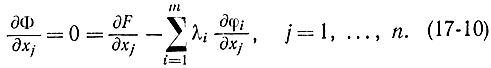
Будем считать, что эти уравнения имеют единственное решение х при любом к из δ-окрестности λ_опт. Тогда точку максимума х_опт можно рассматривать как функцию к и для δ-окрестности λ_опт можно записать:

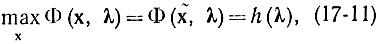
т. е. максимум по х будет функцией кλ. Очевидно, что

так как при λ = λ_опт и х = х_оптφ_i (х) = b_i и

Обозначим допустимую область значений х, ограничениям b - φ (х) = 0, через G. Тогда

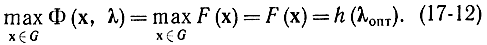
Область G в соотношении (17-12) составляет часть от общей области изменений х, по которой ищется максимум в соотношении (17-11). Поэтому

Эта запись означает, что h(λ) имеет минимум в точке λ_опт. Но так как для х и λ, удовлетворяющих условию (17-22), h(λ) = Φ (х, λ), то выражение (17-13) утверждает, что Φ (x, λ) имеет минимум по к в точке x_опт при условии выполнения (17-10).

Задача минимизации Φ (х, λ) по к при ограничениях (17-10), которые для каждого к определяют соответствующее х, называется задачей, двойственной к задаче отыскания максимума F (х) при ограничениях φ_i (х) = b_i (i = 1, ..., m):

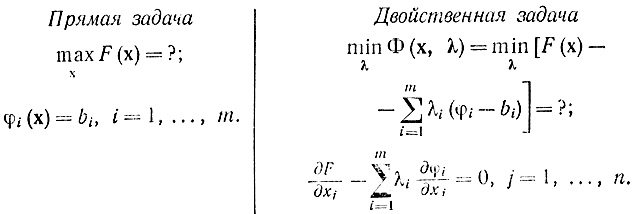
Двойственные задачи обладают тем свойством, что в окрестности х_опт в соответствующих ограничениях

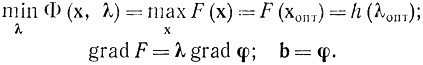
Но в соответствии с равенством (17-11)

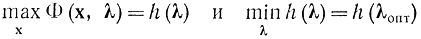
и поэтому

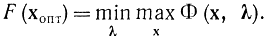
Это важнейшее соотношение означает, что задача оптимизации функции при ограничениях сводится к решению задачи на минимакс. Оно смыкается с теорией игр и утверждает, что задачи на условный

экстремум сводятся к игровым задачам, в частности отысканию, седловой точки. Последнему утверждению можно придать более четкую форму. Если рассматривать малую окрестность точки [х_опт, λ_опт] в (n + m)-мерном пространстве, то в силу того, что Φ (х, λ) имеет максимум по х, для любого к из этой окрестности можно написать:

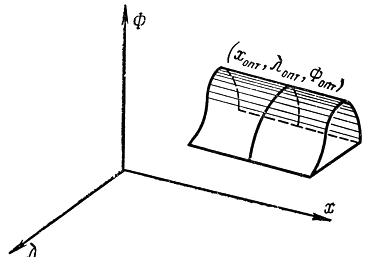
Рис. 17-7. Вырожденная седловая точка

Далее, Φ (х_опт, λ) = F (х_опт), так как х_опт ∈ G. Поэтому Φ (х_опт, λ) = F (х_опт, λ). С учетом этого и соотношения (17-14) можем написать:

Тем самым доказано, что функция Лагранжа имеет в оптимальной точке (х_опт, λ_опт) седловую точку, правда, вырожденного типа, так как справа стоит знак строгого равенства (рис. 17-7).

Точка (х_опт, λ_опт) функции двух векторных переменных Ψ (х, λ) называется седловой, если удовлетворяются соотношения

Заметим, что знак "=" можно заменить более широким знаком "≤".

Классические методы оптимизации функции при наличии ограничений, так же как и классическое вариационное исчисление, в принципе позволяют определять экстремум функции при ограничениях в виде нестрогих равенств, и, в частности, при требовании не отрицательности переменных. Однако это сопряжено с возрастанием трудоемкости вычислений. Рассмотрим вначале случай не отрицательности переменных. Пусть имеется задача оптимизации вида

Допустим, что максимум достигается в точке х_опт, которая лежит внутри или на границе области допустимых значений. Первоначально исследуют все внутренние точки положительного октанта n-мерного пространства и в них вычисляют значения функции цели z. Затем исследуют границу положительного октанта, причем на первом этапе приравнивают нулю одну переменную, решают задачу на оптимум с оставшимися n — 1 переменными, и m ограничениями и вычисляют значение функции цели для каждого решения. Так как переменных n, то на первом этапе необходимо решить n задач с n — 1 переменными и m ограничениями. На втором этапе приравнивают нулю каждые две координаты и решают задачу с n — 2 переменными и m ограничениями. Можно показать, что число таких задач будет n!/2! (n — 2)!. В последующих задачах нулю приравниваются три, четыре и т. д. координаты. Отсюда сразу видна трудоемкость такого вычислительного процесса. Если не все переменные подчинены условию не отрицательности, то нулю приравниваются только те, для которых это требование имеет место.

Теперь рассмотрим случай, когда нет условий не отрицательности, но некоторые из ограничений имеют форму неравенств. Пусть

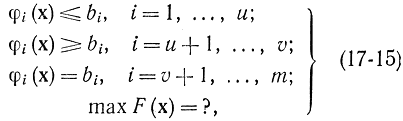
т. е. v ограничений имеют форму неравенств, остальные m — v — форму равенств. Добавим v переменных x_φi≥0 которые сводят неравенства (17-15) к равенствам вида

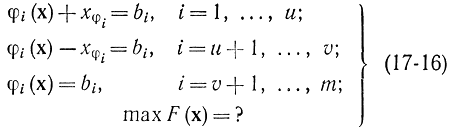
Теперь задача свелась к ранее рассмотренной: ограничения заданы в виде строгих равенств, но имеется требование не отрицательности u + v переменных x_φi. Заметим, что условие g_i(x) ≥ b_i эквивалентно x_φi≥0 (i = 1, ..., v), а условие g_i (х) ≥ b_i эквивалентно x_φi≥0 (i = u + 1, ...., vi). Экстремум может достигаться внутри неотрицательного октанта u-мерного пространства, где x_φi>0, и на его границах, где одно или несколько x_φi=0. Рассмотрим вначале вариант с x_φi>0. Функция Лагранжа для уравнений (17-16) будет иметь вид:

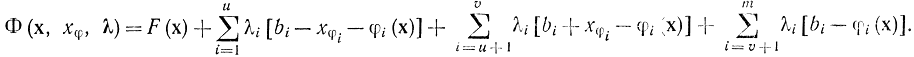
Для точки оптимума частные производные от этой функции по всем переменным, в том числе и по x_φi, должны равняться нулю. Поэтому

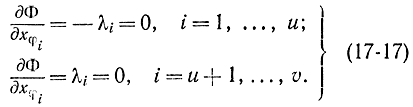
Эти соотношения означают, что если в точке экстремума x_φi>0, то соответствующие λ_i = 0, т. е. ограничения, которые в точке экстремума имеют вид строгих неравенств, можно не учитывать. При движении по границе, где некоторые x_φi = 0, соответствующие ограничения следует учитывать и для них λ_i ≠ 0. По существу доказано очень важное соотношение, что в точке оптимума или вспомогательные переменные x_φi = 0, или соответствующие множители Лагранжа λ_i = 0, т. е.

или

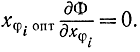
Таким образом, вначале просматривают внутреннюю часть области положительного октанта v-мерного пространства x_φi, т. е. по существу отбрасывают все ограничения в форме неравенств (v штук), ищут решение и вычисляют значение z. Затем поочередно подключают одно соотношение, эквивалентное x_φi = 0, далее по два соотношения и т. д. и каждый раз вычисляют значения z. Наибольшее из этих z соответствует точке экстремума.