17-6. Квадратичное программирование

Рассмотрим здесь только задачи нелинейного программирования, относящиеся к задачам квадратичного программирования, в которых F(x) является квадратичной функцией

где С - симметричная положительно полуопределенная матрица, а функции в ограничениях представляют собою линейные функции:

где a_i = || a_i1, a_i2,...,a_in ||. Сама задача квадратичного программирования может быть записана в виде

где A = ||a_ij||, b = || b_i||.

Все коэффициенты в формулах (17-42), (17-43) могут быть произвольными, за исключением коэффициентов матрицы С. Симметричность этой матрицы необходима для квадратичности функции цели, чтобы члены a_kl, x_k, x_l и a_lk, x_l, x_k равнялись друг другу и объединялись в один 2a_klx_kx_l.

Можно доказать [Л. 96], что если С - положительно полуопределенная матрица, т. е. хСх ≥ 0 для всех х, то функция Q (х) = хСх - выпукла.

Квадратичные программы могут быть записаны в одном из трех видов:

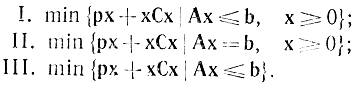
Очевидно, что с помощью уже применявшихся приемов можно любую из трех задач свести друг к другу. Функция Лагранжа для них запишется как

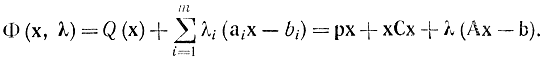
Обозначив

получим:

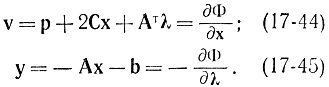
Условия Куна - Таккера для этих трех задач имеют вид:

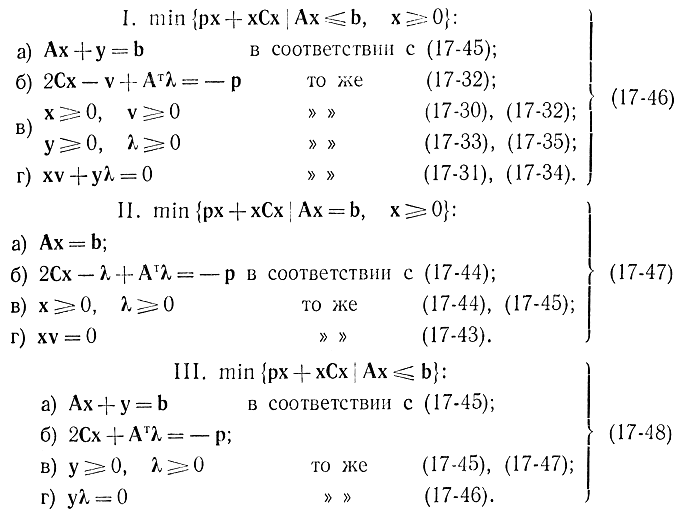
Соотношение (17-48, б) следует из того, что при отсутствии ограничений на знак переменной "работают" классические методы и

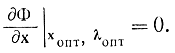
С помощью соотношений (17-46), (17-48), выражающих условия Куна - Таккера, по существу нахождение я-мерного вектора х свелось к нахождению двух n-мерных векторов х и v и двух m-мерных векторов λ и y, удовлетворяющих или условиям (17-46), или (17-47), или (17-48). Все значение теоремы Куна - Таккера заключается в том, что задача нелинейного программирования сводится к решению систем уравнений (17-46) - (17-48). Для квадратичного программирования условия Куна - Таккера были получены Баранкиным и Дорфманом. Надо заметить, что они имеют различный характер. Так, соотношения (17-46, а), (17-48, а) и (17-46, б), (17-48, б) представляют собою линейные алгебраические уравнения, тогда как условия (17-46, г), (17-48, г) носят комбинаторный характер. Условия (г) требуют, чтобы из каждых двух ограниченных переменных x_j и v_j, общим числом 2n, или λ_i и y_i общим числом 2m, по крайней мере одна равнялась нулю. Поэтому все те решения систем (17-46, а - в), (17-48, а - в), которые образуют множество возможных решений уравнений (17-46,г),(17-48,г), характеризуются тем, что имеют самое большее столько компонент, отличных от нуля, сколько имеется в (17-46,а,б) (17-48,а,б) ограничений в форме равенств, т. е. m + in. Эти решения являются базисными, и только среди них следует искать такое, которое бы удовлетворяло условиям (г). Поэтому для задач (17-46) - (17-48) можно применять видоизменный симплекс-метод, который подробно будет изложен в методе Баранкина и Дорфмана.