17-7. Метод Баранкина и Дорфмана

Этот метод применяется к задаче квадратичного программирования, сформулированной в виде I,

В данном случае условия Куна - Таккера в соответствии с формулами (17-46) запишутся в виде

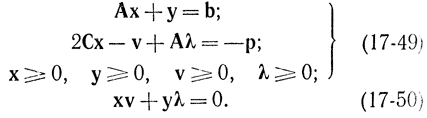
Отметим, что соотношение (17-50) может выполняться только для допустимого базисного решения системы (17-49), которое характеризуется той особенностью, что из 2 (n + m) ограниченных по знаку переменных х, v, y, λ самое большее N переменных, где N - n + m - число равенств в этой системе, отличны от нуля.

Идея метода Баранкина и Дорфмана заключается в том, что процедура последовательного отыскания решения начинается с базисного решения системы (17-49), которое не обязательно удовлетворяет условию (17-50). Затем с использованием симплекс-метода добиваются равенства нулю выпуклой функции xv + yλ.