18-2. Нелинейное и целочисленное программирование

Можно показать, что любая задача выпуклого нелинейного программирования может быть приближенно сведена к соответствующей задаче целочисленного программирования. Допустим, что функция цели F (х) имеет вид сепарабельной функции

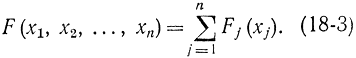
Будем считать, что каждое слагаемое F_j (x_j) представляет собой выпуклую функцию, и в дальнейшем изложении опустим индекс j, используя обозначение F (х). Разобьем весь интервал изменения x (рис. 18-5) на участки Δ_k= [d_k-1, d] длиной h_k = d_k -d_k-1. Если ввести новые переменные, равные длине пересечения отрезка [0, х] с отрезком Δ_k, т. е.

где

то

При этом функция F (х) может быть приближенно заменена на

Для выпуклой функции F (х) коэффициенты c_k образуют монотонную последовательность

Задача минимизации функции F(x), задаваемой формулой (18-6) при условиях (18-4) и (18-5), является задачей частично целочисленного программирования. Частичную целочисленность задачи можно пояснить следующим образом. Прежде всего, заметим, что оптимальное решение линейной задачи можно записать в виде

где y₁=h₁, y₂=h₂,...,y_k0-1=h_k0-1, 0<y_k<h_k0 а все y_k для k > k₀ равны нулю. Здесь по существу намечена некоторая процедура поиска оптимального решения. В начале y₁ увеличивается до своего максимального значения. Если экстремум не достигнут, то, зафиксировав y₁ на максимальном значении, увеличивают y₂ от нулевого значения y₂ = 0 до максимального и т. д., пока не дойдут до y_0k. Если y_0k взять максимальной, то нарушится соотношение (18-8). Необходимо эту переменную уменьшить до значения, удовлетворяющего соотношению (18-8). Остальные y_k (k > k₀) следует положить равными нулю, что является следствием выпуклости функции цели, которая обусловливает соотношения (18-7). В соответствии с этим условием нецелесообразно брать переменную y_k+1 отличную от нуля, пока y_k не достигла своего максимального значения. Формально последнее утверждение может быть записано с помощью следующих логических соотношений, 1 носящих альтернативный характер:

Это условие в рассмотренной выше задаче минимизации (18-6) при условиях (18-4) и (18-5) не является дополнительным и автоматически выполняется при соблюдении условий (18-4) и (18-5).

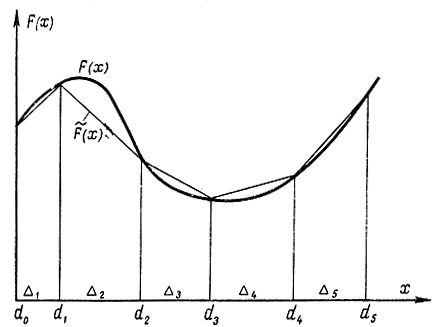
Рис. 18-5. Пояснение к методу сведения задач не выпуклого программирования к задачам целочисленного программирования

Рассмотрим теперь не выпуклую функцию F (х) (рис. 18-5). Опять заменим исходную функцию цели приближенно кусочно-линейной функцией в соответствии с формулой (18-6). Однако при этом не соблюдается условие монотонности коэффициентов с_k [см. формулу (18-7)]. Можно попытаться довести до верхней границы вначале значение y_k соответствующее наименьшему c_k, затем значение y_k соответствующее следующему по величине c_l и т. д., однако при этом отрезки Δx, из которых комплектуется оптимальное значение х, получаются несвязными. Для обеспечения их связности необходимо условие (18-9) ввести как обязательное, так как оно в данном случае автоматически не выполняется. Сведем его к целочисленной программе. Для этого воспользуемся дополнительными переменными

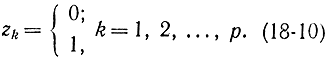
Тогда условие (18-9) можно заменить соотношениями

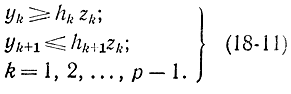
Нетрудно убедиться, что z_k = 1 соответствует достижению y_k своей верхней границы, так как первое соотношение (18-11) превращается в y_k≥h_k т. е. y_k = h_k [переменная y_k по условию (18-4) не может быть больше h_k]. Значение z_k соответствует условию y_k < h_k, так как второе соотношение (18-11) превращается в y_k+1 ≤ 0, которое в силу (18-4) означает, что y_k+1 = 0. Далее, замечая, что ограничения, наложенные сверху на y_k в соотношениях (18-4), уже содержатся в формулах (18-11), кроме ограничения на y₁ можно заменить ограничения (18-4) и (18-11) на следующие:

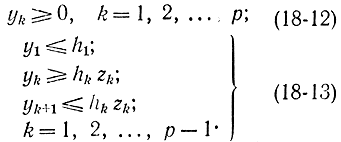
В итоге исходная задача не выпуклого программирования свелась к задаче целочисленного программирования

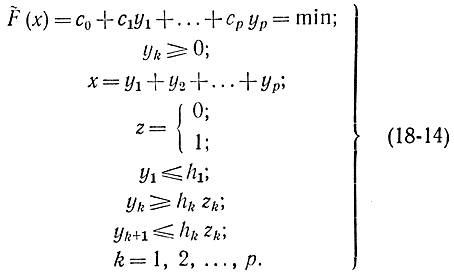
Кроме того, если в исходной нелинейной программе имеют место ограничения

их следует добавить к ограничениям (18-14).

Приведенный выше способ сведения не выпуклой нелинейной программы к частично целочисленной программе реализуется за счет введения большого числа дополнительных переменных и ограничений.