18-1. Особенности задач целочисленного программирования

Характерная особенность общей задачи целочисленного программирования заключается в ее нерегулярности. Под регулярностью понимают совокупность необходимых и достаточных условий экстремума, которые позволяют создать конечную процедуру его отыскания. Условиям регулярности удовлетворяют задачи линейного и выпуклого программирования. В регулярных задачах локальный экстремум совпадает с глобальным. Указанные выше обстоятельства определяются характером области допустимых значений, которая становится многосвязной из-за требования целочисленности (дискретности), а также не выпуклой. Несовпадение целочисленного и не целочисленного экстремумов иллюстрируется примером.

Пример 18-1. Требуется найти решение следующей задачи целочисленного программирования:

При целочисленности переменных максимум 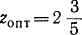достигается в точке x_1опт=3, х_2опт=2 в то время как при исключении этого требования z_опт = 3 в точке 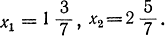. Округление результата до целых не дает оптимума исходной задачи, как это видно из рис. 18-3. Заметим, что условие целочисленности z при снятии этого требования к переменным х₁ и х₂ определяет оптимум при других значениях x₁ и х₂.

Из этого простейшего примера виден комбинаторный характер задач целочисленного программирования, который часто требует прямого перебора. Покажем, как задача дискретного не целочисленного программирования может быть сведена к задаче целочисленного программирования [Л. 97]. Допустим, имеется задача математического программирования в виде

Будем считать что переменная x_j0 может принимать только одно из заданного множества значений

Введем дополнительные булевы переменные y₁, y₂,...,y_p и запишем условие дискретности для х_j0 в вид

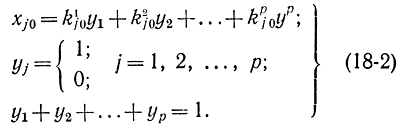
Последнее соотношение требует, чтобы только одна переменная y_v была отлична от нуля. Нетрудно убедиться, что формулы (18-2) обеспечивают дискретность переменной x_j0. Таким образом, путем введения булевых переменных y_v можно всегда свести не целочисленную дискретную задачу математического программирования к целочисленной. Как видно, соотношения (18-2) представляют собой p-кратную логическую альтернативу:

Для лучшего понимания связи задач целочисленного программирования с задачами на многосвязных и не выпуклых областях покажем, как эти последние сводятся к задачам целочисленного программирования. Пусть допустимая область изменения переменной x_j0 многосвязная и задается соотношениями

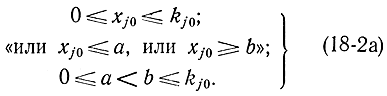
Введем дополнительную булеву переменную y_j0, которую не будем включать в функцию цели, а заменим рассмотренные соотношения следующими:

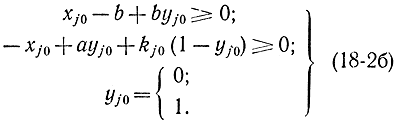
Очевидно, что соотношения (18-2a) и (18-26) эквивалентны. Действительно, когда y_j0 = 1, то (18-26) сводится к x_j0 ≥ 0 и x_j0 ≤ а; когда y_j0 = 0, то к x_j0≥b и x_j0≤k_j0. Таким образом, много связность области допустимых значений легко учитывается введением дополнительных булевых переменных. Этот метод без труда распространяется на случай многих переменных.

Процедура сведения не выпуклой области изменения переменных к стандартным ограничениям состоит в следующем. Область разбивается на выпуклые подобласти, и между некоторыми парами их вводятся альтернативные условия (дизъюнкции). Для каждой подобласти определяется верхняя граница и вводятся дополнительные ограничения, включающие для каждой пары подобластей булевы переменные.

Пример 18-2. Рассмотрим процедуру сведения задачи не выпуклого программирования к целочисленному программированию. Пусть область допустимых значений задана системой неравенств

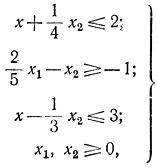
Соответствующая область представлена на рис. 18-4. Первая и вторая пара неравенств образуют выпуклые подобласти х₁ и х₂ с учетом не отрицательности переменных с верхними границами x_1макс и x_2макс соответственно. Введение булевой переменной y приводит к дополнительным неравенствам

Здесь каждое условие относится ко всем неравенствам соответствующей области.

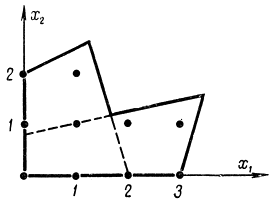
Рис. 18-4. Пример не выпуклой области, состоящей из выпуклых многогранников

Нетрудно убедиться, что аналогичный способ применим в случае числа переменных, большего двух.