а) Задача планирования перевозок

Классическим образцом этой группы задач является транспортная задача, известная еще из гл. 14:

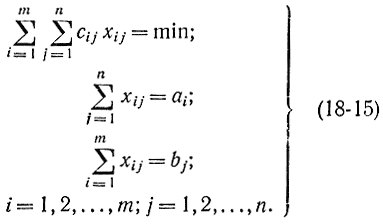
При условии целочисленности исходных данных: наличия товара a_i (i = 1, 2, ..., m) на i-м складе и спроса b_j (j = 1, 2, ..., n) на j-м пункте потребления эта задача решается целочисленно любым способом: симплекс-методом, методом динамического программирования и принципа максимума. Такая особенность данной задачи определяется свойством ее матрицы. Аналогичным свойством обладают и другие задачи, в том числе задача о назначениях, которая сводится к транспортной, задачи о максимальном потоке и потоке минимальной стоимости [Л. 97].

Транспортная задача имеет много модификаций и обобщений (иногда ее называют обобщенной транспортной задачей). Рассмотрим одно из них. Предположим, имеется n транспортных линий. По j-й линии необходимо выполнить b_j рейсов. Общее количество транспортных единиц m и каждая из них имеет резерв полезного времени a_i (i = 1, 2, ..., m). На выполнение i-й транспортной единицей j-го рейса требуется время t_ij и затраты c_ij. Если обозначить через х_ij количество рейсов, которое должна выполнить i-я транспортная единица по j-у маршруту, то получится следующая формулировка задачи:

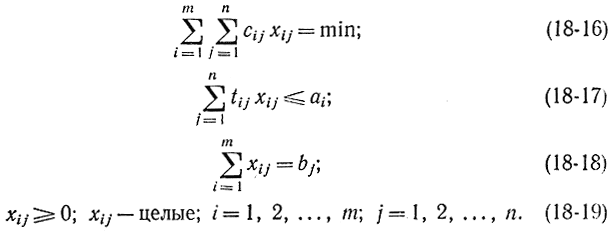
Соотношение (18-18) означает, что все необходимые на j-й линии рейсы должны быть выполнены. Условие (18-17) обеспечивает ограничение по резервам времени, i-й транспортной единицы. В данной задаче целочисленность является обязательным условием.