б) Задача о назначении

Имеется n работ и n кандидатов на выполнение каждой работы. Назначение i-го рабочего на j-ю работу вызывает затраты c_ij (или дает прибыль). Требуется определить наилучшее с точки зрения минимума суммарных затрат распределение рабочих. В комбинаторном смысле задача представляет собой перестановку (р₁, р₂, ..., р_n) чисел (1, 2, ..., n). Каждое назначение одного i-го рабочего на p_i рабочее место описывается соответствием i → p_i. Требуется определить перестановку (p*₁, р*₂, ..., р*_n), при которой

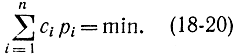
Значение суммы необходимо вычислить по всем перестановкам (р₁, р₂,..., р_n) индексов (1, 2,..., n), например при (1, 2,..., n), (2, 1, 3,..., n). При больших n получается очень сложный вычислительный процесс: сильно возрастает число перестановок [n! = 1 *2*3*...*(n - 1)n].

Посредством булевых переменных

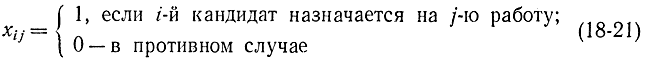
сведем эту задачу к задаче целочисленного программирования вида

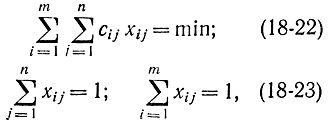
где x_ij - целые.

Геометрически в n²-мерном пространстве каждая перестановка изображается точкой, точки - вершиной n²-мерного куба с единичной длиной ребра. Каждой точке соответствует квадратная (n*n)- матрица X = ||х_ij||. Условия (18-23) означают, что в этой матрице только один элемент в каждой строке и столбце может быть отличен от нуля и его значение равно единице.

Задача о назначении легко сводится к транспортной, если условие (18-21) заменить на требование не отрицательности x_ij ≤ 0 и учесть, что в данном случае m = n и a_i = bi = 1.

Известна квадратичная задача о назначении, в которой требуется определить набор элементов x_ij принимающих значения 0 или 1 при условиях

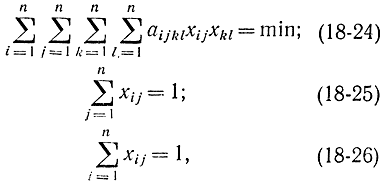
где a_ijkl - некоторые заданные числа. К ней сводится видоизмененная задача о назначениях, когда в функции цели учитывается взаимное влияние назначений i и j, которое считается пропорциональным расстоянию по Хэммингу d_pipj. между соответствующими точками p_i и p_j

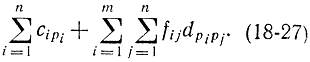
В этом выражении f_ij - заданные величины.

Дальнейшее развитие задачи о назначении заключается в добавлении к классической постановке условия, которое разрешает i-у рабочему назначение только на рабочее место из заданного подмножества S (i). Все остальные рабочие места являются запретными. Это условие легко можно учесть, положив в формуле (18-22) или (18-27) c_ij = ∞ для запретных относительно S (i) элементов j. В этом случае задача о назначении (распределении) или транспортная соединяется с задачей о расписании (см. гл. 14).