г) Задача о покрытии

В задаче о минимальном покрытии требуется при заданном графе Г найти минимальное количество ребер, таких, что любая вершина графа инцидентна (принадлежит) ребру, входящему в покрытие.

Обозначим вершины графа через i (i = 1, 2, ..., m), а ребра через j (j = 1, 2,...,n) и введем матрицу инциденций А = a_ij такую, что

Вводя булевы переменные х_j (j = 1, 2, ..., n) такие, что

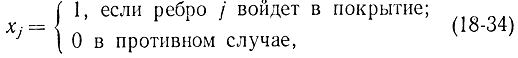
получаем, что задача о минимальном покрытии сводится к линейной задаче целочисленного программирования вида

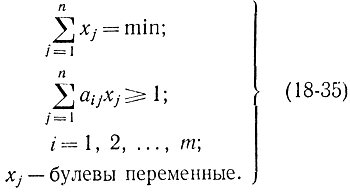
Второе условие (18-35) означает, что каждая вершина инцидентна хотя бы одному ребру.

Существует более общая формулировка задачи о покрытии, когда вместо ребер, составляющих покрытие, фигурируют подграфы исходного графа. Алгебраически она может быть сформулирована следующим образом. Задано конечное множество S = {σ₁, σ₂, ..., σ_m}, состоящее из m элементов, и конечное множество его подмножеств S_j (j = 1, 2, ..., n). Требуется найти минимальное покрытие, т. е. минимальный набор подмножеств S_j, при котором любой элемент множества S принадлежит хотя бы одному из подмножеств S_j. Так же как и ранее, вводится матрица ||a_ij||, каждый элемент которой

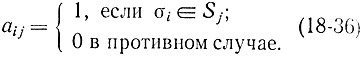
Введем переменные

Если еще ввести веса c_j элементов покрытия, то придем к следующей задаче целочисленного программирования:

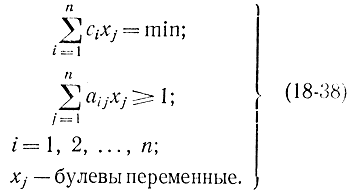
Задаче о покрытии можно дать простую интерпретацию. Допустим, требуется с помощью n малых веток дерева покрыть большую ветку. Для минимального покрытия потребуется наименьшее число веток. Условие покрытия означает, что у покрываемой ветки нет свободных вершин (или ребер).

Помимо задачи о покрытии существует задача об укладке, которая заключается в том, что при заданных множествах S и S_j (где S_j - подмножества S) требуется так разместить подмножества S_j в S, чтобы любой элемент S_j принадлежал бы S, т. е. чтобы свободных элементов множества S было минимальное количество.

Рассмотренные задачи о покрытии и укладке имеют большое прикладное значение при привязке типовых разработок к конкретным системам. В частности, типовая АСУП может быть представлена в виде набора графов (множеств) S_j (типовых решений). Результаты системного обследования конкретного предприятия могут быть представлены в виде графа S. Привязка типовой АСУП к конкретному предприятию заключается в решении задачи минимального покрытия графами S_j графа S.

Интересные приложения находит задача о минимальном покрытии в вопросах синтеза релейных схем [Л. 97].