в) Задача о коммивояжере (бродячем торговце)

Имеется n + 1 городов и заданы расстояния между ними c_ij. Выезжая из одного города (обозначаемого индексом 0), коммивояжер должен побывать в каждом городе по одному разу и вернуться в город 0. Требуется определить порядок, в котором следует объезжать города, чтобы суммарное расстояние было бы минимальным. Если ввести переменные

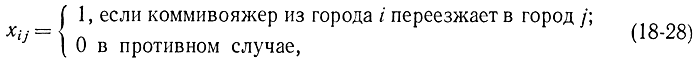
то данная задача сведется к следующей:

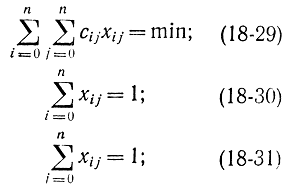
где

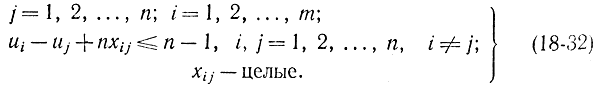
Условия (18-30) и (18-31) означают, что коммивояжер один раз выезжает из каждого города и въезжает в каждый город один раз. Соотношения (18-29), (18-30) и (18-31) определяют задачу о назначении, которая отличается от задачи коммивояжера отсутствием требования цикличности пути решения.

Аналитически требование цикличности записывается в виде (18-32), где переменные u_i могут принимать произвольные вещественные значения. Допустим обратное: имеется подцикл τ с числом ребер k < n, не проходящий через город 0. Складывая все неравенства (18-32) при x_ij = 1 вдоль подцикла τ, получаем противоречивое неравенство: nk ≤ (n - 1) k, так как все разности u_i-u_j уничтожаются. Таким образом, условие (18-32) не допускает цикла, не проходящего через город 0. Покажем, что можно выбрать значения uif при которых для цикла, проходящего через город 0 (i = 0), удовлетворяются соотношения (18-32). Для этого предположим, что u_i = p, если город i посещается на р-м шаге, где р = 1, 2, ..., n. Очевидно, при этом u_i-u_j≤n-1 для любых i и j. Тем самым доказано, что соотношения (18-32) для x_ij = 0 удовлетворяются. При x_ij = 1 эти соотношения превращаются в равенства. Действительно, учитывая (18-28), имеем:

Задача о коммивояжере из-за условия цикличности не сводится к транспортной и является типичной задачей дискретной математики с резко выраженными комбинаторными свойствами.