18-4. Методы отсечения

В основном данный параграф будет посвящен линейной задаче целочисленного программирования и первому алгоритму Гомори [Л. 97], который заложил фундамент теории целочисленного программирования. В заключение будут изложены приемы решения целочисленной задачи с линейной функцией цели и нелинейными ограничениями.

Для удобства изложения методов целочисленного программирования используют специфические обозначения, на которых целесообразно прежде всего остановиться. Задачу целочисленного программирования рассмотрим в виде

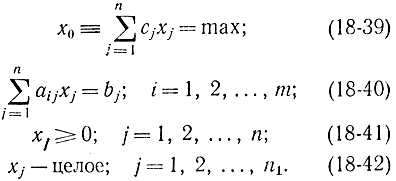
При т₁=т задача (18-39) - (18-42) является полностью, а при n₁ < n частично целочисленной задачей линейного программирования. По аналогии с задачей линейного программирования (см. гл. 14) введем ряд понятий. Множество наборов (х₁, х₂,..., x_n) удовлетворяющих условиям (18-40) - (18-42), называется областью определения или допустимой областью задачи целочисленного программирования и обозначается через L^ц Для сокращенного обозначения задачи (18-39) - (18-42) применяется запись (L^ц, с), где с - вектор-столбец, состоящий из элементов c_i. Оптимальное решение или оптимальный план обозначается через х (L^ц, с). Наряду с оптимальным планом x_опт = (x_1oпт, x_2опт,...,x_nопт) будет рассматриваться расширенный оптимальный план

где

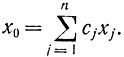
Сокращенно оптимальный расширенный план обозначается как

В целочисленном программировании рассматриваются целочисленные многогранники, под которыми понимаются многогранники с целочисленными вершинами, и целочисленные симплекс-таблицы, состоящие из целочисленных элементов. Заметим, что множество точек, ограниченное целочисленным многогранником, не обязательно состоит из целочисленных точек, требуется только целочисленность вершин (крайних точек) многогранника.