а) Общая идея методов отсечения

Основная идея методов отсечения заключается в построении такой эквивалентной задачи линейного программирования (А, с), при которой исходная задача целочисленного программирования (L^ц, с) сводится к ее решению. Иногда это называют линейной аппроксимацией целочисленного программирования (L^ц, с).

Введем понятие правильного отсечения, физически означающее выбор такой гиперплоскости, которая разделяет оптимальные решения целочисленной линейной задачи х (L^ц, с) и задачи линейного программирования х (L, с), причем последняя не удовлетворяет условию целочисленности

Математически правильное отсечение означает выбор такого числа β, при котором неравенство

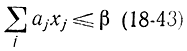
выполняется при условиях

где а - вектор-строка, состоящая из элементов a_j.

Метод отсечений позволяет построить процедуру последовательного выделения оптимального решения целочисленной задачи по известному решению соответствующей линейной задачи, в которой исключены требования целочисленности. Эта процедура решения задачи (L^ц, с) может быть описана следующим образом:

1. На k-м этапе решается вспомогательная задача линейного программирования (L_k, с), k = 0, 1, 2, где L₀ = L.
2. Если на k-м этапе оптимальное решение х (L_k, с) удовлетворяет условию целочисленности, то оно будет также оптимальным решением х (L^ц₀, с) исходной задачи (L^ц₀, с), так как на всех этапах множества целочисленных точек совпадают, т. е.
   L^ц₀=L^ц₁=...
   что является специальным условием при отсечении.
3. Если на k-м этапе решение не удовлетворяет условиям целочисленности, то х (L_k, с) не является оптимальным решением исходной целочисленной задачи. В этом случае переходят от k-го этапа к (k + 1) - му, добавляя к линейным ограничениям задачи (L_k, с) условие правильного отсечения
   а^kх≤β^k, (18-46)
   которое превращает многогранник (множество) L_k в многогранник L_k+1. Каждый конкретный метод имеет свой способ задания отсечения, но в алгоритмах Гомори гарантируется конечное число процедур.