б) Первый алгоритм Гомори

В этом алгоритме впервые была реализована идея метода отсечения. Он дает конечную процедуру решения полностью целочисленной задачи линейного программирования, заданной в виде

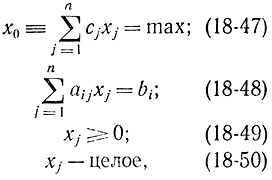
где i = 1, 2 ..., m; j = 1, 2, ..., n.

Выразим функцию цели x₀ и все переменные x₁ ..., x_n через не базисные переменные x_j (j ∈ N), где N - множество i индексов, соответствующее не базисным переменным

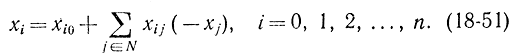
Здесь используются для удобства другие по сравнению с гл. 16 обозначения: x_i0 = b'_i - свободные члены; x_ij = a'_ij - коэффициенты при j-й не базисной переменной; x_0j= с'_j, причем x_i0 = 0 при i > m, а для i > m

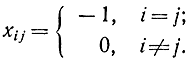
Кроме того, нулевые компоненты в векторах иногда будут опускаться, например, для вектора-столбца

В дальнейшем в формуле (18-51) будет иногда меняться порядок нумерации и не обязательно m первых переменных x_i0 будут отличны от нуля. Обозначим через [x] целую часть вещественного числа, равную наибольшему целому числу, не превышающему х. Дробная часть числа определяется как {x} -х-[х]. Допустим, что х (L, с) - решение задачи (18-47) - (18-49) без требования целочисленности. Оно получается приравниванием нулю не базисных переменных в соотношении (18-51), соответствующем последнему этапу симплекс-процедуры x_i = x_i0. Считая (18-51) решением задачи линейного программирования без требования целочисленности, запишем его в виде

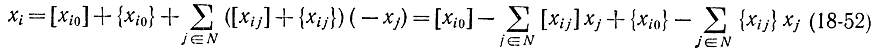
Для любого целочисленного решения, задаваемого формулой (18-51), величина

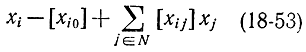
должна быть целой. Но отсюда с учетом (18-52) следует, что

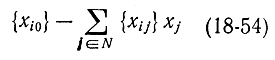
также должна быть целой. Так как величина 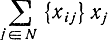не может быть отрицательной, потому что {x_ij}≥0, x_j≥0 и 0 <{x_i0}<1 величина (18-54) не может быть положительным целым числом. Следовательно, любое допустимое решение x_j целочисленной задачи (18-47) - (18-50) должно удовлетворять неравенству

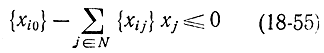
или

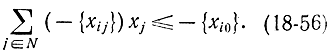
Нетрудно убедиться, что решение задачи (18-47) - (18-49) без требования целочисленности не удовлетворяет неравенству (18-56). Тем самым условие отсечения (18-44) удовлетворяется.

Соотношение (18-56) определяет гиперплоскость, которая отсекает не целочисленное решение, оставляя по другую сторону целочисленное решение. Это правило отсечения и составляет основное содержание метода Гомори. Его следует добавить к ограничениям (18-48), тогда их станет m + 1. Для соотношения (18-56) можно ввести дополни-тельную переменную

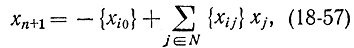
которая будет целочисленной, благодаря чему задача останется полностью целочисленной. Задачу с добавлением ограничения (18-57) будем называть расширенной. Можно показать, что для ее решения нет необходимости решать все заново. Действительно, если обозначить через А_б матрицу, состоящую из r линейно-независимых столбцов матрицы А =|| a_ij|| исходной системы (18-48), тогда базисное, но не обязательно допустимое решение (18-51) может быть записано в виде

где не базисные переменные x_j (j ∈ N) приравнены нулю.

Обозначим через А_б1 матрицу, соответствующую базису расширенной задачи

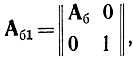
В эти матрицы добавлен вектор-столбец

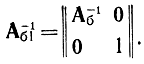
соответствующий дополнительному ограничению (18-57). Теперь базисное решение расширенной задачи запишется как

причем для оптимального решения не целочисленной линейной задачи

где

- вектор оценок, компоненты которого состоят из коэффициентов функции цели при базисных переменных. Это базисное решение недопустимо, так как

Соответствующий базису А_б1 вектор оценок для расширенной задачи будет равен || с_б, 0 ||. Далее введем вектор

где a_j - j-й вектор-столбец матрицы А и величины z_j = с_бx_j, причем x_0j = c'_j - c_j. Тогда получим, что величины c'_j, равные коэффициентам функции цели при j-x переменных для расширенной задачи, будут такими же, как и для оптимального решения линейной задачи (18-47) - (18-49) без условия целочисленности (18-50), так как векторы x_j ∈ N для расширенной задачи, которые обозначим через x⁽¹⁾_j, будут равны:

Так как мы исходим из того, что получено оптимальное решение линейной задачи без требования целочисленности, то в соответствии с результатами гл. 16 должно быть z_j - c_j ≥ 0. Если при этом учесть, что вектор оценки для расширенной задачи имеет вид || с_б, 0 ||, то получится базисное, но недопустимое решение расширенной задачи, для которого z_j - c_j ≥ 0. Но отсюда следует, что выгоднее для поиска решения расширенной задачи использовать двойственный, а не прямой симплекс-метод. При этом, грубо говоря, процедура поиска сокращается в два раза, так как при использовании двойственного симплекс-метода величины z_j - c_j, равные свободным коэффициентам ограничений двойственной задачи (и коэффициентам функции цели прямой задачи), остаются неотрицательными, что указывает на то, что на всех этапах двойственного симплекс-метода имеет место базисное решение двойственной задачи, не допустимое для прямой. Если применять прямой симплекс-метод, в данном случае пришлось бы выполнить обе половины процедуры, т. е. искать решения среди базисных. Это повлекло бы за собой изменение знаков коэффициентов z_j - c_j и потерю базисного начального решения двойственной задачи.

Чаще всего для решения расширенной задачи двойственным симплекс-методом достаточно одной итерации. Если решение получится не целочисленным, его повторяют, добавляя новые дополнительные ограничения типа (18-57), выбирая другое значение i. Эта процедура продолжается до тех пор пока не будет получено оптимальное решение целочисленной задачи (18-47) - (18-50). Таким образом получается итерационная процедура отыскания оптимального решения целочисленной задачи линейного программирования. На первом этапе решается задача Q₀ линейного программирования без требования целочисленности. Если полученное решение допустимо для целочисленной задачи, то оно является оптимальным. В противном случае переходят ко второму этапу, где решают двойственным симплекс-методом задачу Q₁ линейного программирования без требования целочисленности, которая имеет на одно ограничение и одну переменную больше, чем задача Q₀. После этого или процесс прекращают, если полученное решение допустимо для целочисленной задачи, или переходят к решению следующей задачи Q₂ без требования целочисленности, которая получается в результате построения нового отсечения, и т. д. Если ввести индекс k для обозначения номера очередного этапа (k = 0, 1, ...), то, очевидно, что на первых этапах число дополнительных ограничений будет расти с ростом к. Но можно утверждать, что какое бы большое k ни было, общее число различных дополнительных ограничений (отсечений) в задаче Q_k не может превышать n + 1, так как общее число переменных в исходной задаче равно n и, по-видимому, можно ожидать, что общее число отсекающих гиперплоскостей будет равно n (далее они будут повторяться). Дело в том, что вспомогательная переменная х_{n+k_1} которая является базисной в задаче Q_{k_1} при построении задачи Q_k может быть опущена, так как не обязательно,чтобы выполнялось ограничение, соответствующее этой переменной. Результаты решения задачи Q_{k_1} учитываются в задаче Q_k использованием переменных x_j, которые входили в оптимальное решение задачи Q_{k_1} Исключение лишнего ограничения осуществляется вычеркиванием в симплекс-таблице, составленной для задачи Q_k-1, строки и столбца, соответствующих переменной x_{n+k_1} причем имеется в виду симплекс- таблица типа (n - 1) * (m + 1). В силу того что исходная задача содержит n переменных, после исключения из задачи Q_k-1 ограничений, соответствующих вспомогательным переменным x_n+v, вошедшим в оптимальное базисное решение этой задачи, получается задача, содержащая не более n дополнительных ограничений. С переходом от нее к задаче Q_k необходимо добавить одно ограничение, поэтому общее число ограничений в задаче Qk может превосходить общее число ограничений в задаче Q₀ не более чем на n + 1. Гомори доказал, что для случая целочисленных элементов матрицы А и компонент вектора b решение исходной задачи целочисленного линейного программирования можно получить, решив конечное число задач Q_k.

Процедура классического метода Гомори отличается от выше рассмотренной двумя положениями. Во-первых, необязательно решать исходную задачу линейного программирования. На первом этапе можно использовать любое базисное, но необязательно допустимое решение, для которого все z_j - c_j ≥ 0. Во-вторых, в алгоритме Гомори на каждом этапе ищется решение так называемой лексикографической задачи линейного программирования (j-задачи), что позволяет выбирать решение при условии неоднозначности задачи. Вектор х = (x₁, х₂, ..., х_n) = ||x_j|| называется лексикографически положительным, т. е. х > 0, если первая отличная от нуля его компонента положительна, т. е. x_i ≥ 0, где l = min {j/x_j≠0}.

Расширенный план х_опт (допустимое решение) называется лексикографически оптимальным, если для всех расширенных планов х разность х_опт - х лексикографически положительна: х_опт - х₀.

В рассмотренных выше процедурах отсутствует правило выбора переменной и соотношения типа (18-52), с помощью которого строится правильное отсечение, когда несколько компонент оптимального вектор-решения исходной линейной задачи не целочисленны. В алгоритме Гомори используется первая по номеру не целочисленная переменная. Если переписать соотношения (18-52) для k-й итерации (этапа) Q_k в виде

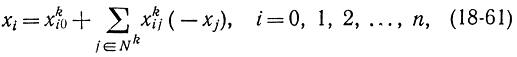
то правило выбора очередной переменной в алгоритме Гомори запишется как

и правильное отсечение на (k + 1)-м этапе запишется в виде

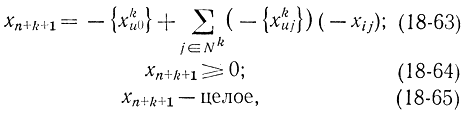
Причем функция цели также включена в систему (18-61) под номером i = 0. Таким образом, если функция цели имеет на нулевом этапе нецелочисленное значение, то первое отсечение строится с ее учетом. Если гарантирована целочисленность функции цели, то правило (18-62) запишется в виде

Для не особого случая задачи линейного программирования, когда множество оптимальных планов не пусто и ограниченно, всегда существует лексикографический оптимальный план задачи.

Лексикографический симплекс-метод, или l-метод, отличается от симплекс-метода главным образом правилом для определения вектора, вводимого в базис, которое на следующем шаге обеспечивает лексикографичность симплекс-таблицы [Л. 97]. Можно показать, что если множество допустимых значений исходной линейной задачи выпукло и ограниченно, то строки симплекс-таблицы

могут быть лексикографически упорядочены, т. е. любой столбец лексикографически положителен:

Как всегда, из базиса выводится наибольшая по модулю отрицательная переменная х_р (р ∈ N_б).

Приведенная выше симплекс-таблица приспособлена для двойственного симплекс-метода и имеет n + 1 строк и m столбцов с первой строкой, состоящей из свободных членов x_0j. Для определения вводимой в базис переменной последовательно повторяется процедура определения максимальных отношений. Сначала вычисляется

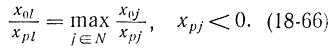
Если l единственно, j-й столбец вводится в базис. В противном случае для тех j, для которых выполняется (18-66), снова вычисляют

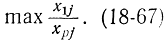
Если максимум достигается при одном j, этот столбец вводится в базис. В противном случае повторяют процесс определения максимума для тех j, для которых он достигается, т. е.

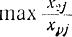
Тем самым однозначно определяется столбец x_l вводимый в базис, так как иначе один вектор x_j оказался бы пропорционален другому, что невозможно из-за условия независимости векторов ау, составляющих матрицу А_б = || а_j||, если учесть, что

В результате этого будет найден вектор

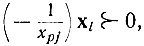
такой, что

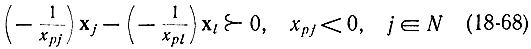
или

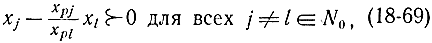
так как в соответствии с формулой (18-67) выбран вектор x_l с минимальным значением x_0l/|x_0l|.

Левая часть формулы (18-69) определяет все компоненты вектора x_j следующего этапа Q₂ за исключением р-й компоненты. Вектор x_j определяет j-й столбец новой симплекс-таблицы, которая получается из предыдущей исключением х_р из базиса и включением в него х_l. Эта симплекс-таблица согласно (18-69) за вычетом р-й строки будет лексикографически правильной. Ранее было доказано, что исходные симплекс-таблицы задач Q₀ и Q₁ были лексикографически правильными. Проверим, не нарушит ли р-я компонента лексикографичность вектора x_j. Компонента р столбца x_j равна x_pj/x_pl. А вектор-столбец симплекс-таблицы, соответствующий переменной х_р, ставший теперь не базисной переменной, имеет компоненты

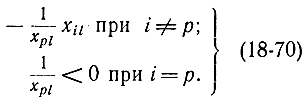
Вектор x_l=||x_il|| был лексикографически положителен, и его первая, отличная от нуля компонента была положительна. Следовательно, этой компонентой не могла быть xpU которая меньше нуля. Поэтому вектор-столбец, соответствующий переменной х_р, благодаря условиям (18-70) будет лексикографически положителен. Так как х_рl не является первой ненулевой компонентой х_l то в силу (18-70) x≥0, j≠l∈N. Кроме того, для всех j, входящих в новое множество N не базисных переменных, полученное из N исключением j = l и добавлением соответствующего х_р имеем х_j≥ 0.

Далее, в соответствии с условиями (18-70)

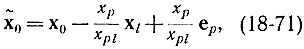
где е_р - единичный - вектор с единичной компонентой. Отсюда

Это означает, что при лексикографическом симплекс-методе вектор х0 лексикографически уменьшается.

Данное утверждение справедливо для любого этапа k, так как в задаче Q_k+1 (n + 1)-я компонента исходного вектора х₀ равна соответствующим компонентам вектора х₀ в задаче Q_k.

При добавлении на каждом шаге ограничений, осуществляющих очередное отсечение, число компонент вектора x_j увеличивается. В результате исключения ограничений, вспомогательные переменные которых вошли в базис, условие x_j≥0, j ∈ N не нарушится. Действительно, ранг матрицы X = || x_ij || = || x_j || = || a_ij || в задаче (18-61), состоящий из r+1 столбцов x_j, равен r + 1. После каждого этапа (итерации) первые n + 1 уравнений останутся такого же типа, как и (18-61). Поэтому мало вероятно, что n + 1 компонент некоторого вектора x_j обратятся в нуль и лексикографическая положительность этого вектора всегда будет определяться n + 1 его первыми компонентами. Это обеспечивает конечность процедуры выбора вектора, вводимого в базис, которая сводится к перебору n строк. Случай, когда все x_pj≥0, j ∈ N, не рассматривается, так как в нем двойственная задача имеет неограниченное решение, а прямая целочисленная задача не имеет допустимого решения

Обозначим симплекс-таблицу, соответствующую k-y этапу, через

где Q_n = {0, 1, ..., n) - множество индексов; N^k₀=Q_n-N^k_б или N^k₀ = {0, 1, ..., n} - N_б, - множество индексов, соответствующее не базисным переменным N_k и нулевой переменной на k-м этапе. Тогда с переходом к (k + 1)-у этапу строка x_n+k+1, задаваемая формулой (18-63), приписывается снизу к таблице T^k. В результате получаем недопустимую только по строке x_n+k+1 и так называемую j-нормальную таблицу, в которой любой вектор-столбец x_j лексикографически положителен:

т. е. первая" ненулевая компонента этого вектора положительна. К этой таблице применим j-метод, причем, как уже указывалось, переменная х_n+k+1 (k ≥ 0) выводится из базиса сразу же после введения ограничения x_n+k+1 ≥ 0, где x_n+k+1 = β^k - a^kx. После вывода переменной x_n+k+1 из базиса соответствующая строка вычеркивается, а после ввода в базис переменной x_l (l≥ n + 1) соответствующая строка не восстанавливается. Размер симплекс-таблицы на каждом шаге ограничен числом (n + 2) * (m+ 1), где n - число переменных x_j в исходной задаче; n - число не базисных переменных на k-м этапе, которое совпадает с числом не базисных переменных в исходной задаче, причем один столбец отводится на свободные члены x_i0 [формула (18-58)], (n + 1)-я строка соответствует переменным х₁, х₂, ...,х_n, одна строка - переменной x_n+k+1 (в момент ее введения в базис). Если в ходе дальнейших вычислений переменная x_n+k+1 снова попадает в базис, то соответствующая строка в симплекс-таблице не восстанавливается и в дальнейших вычислениях эта переменная не участвует.

Такие сокращения вычислительных процедур возможны потому, что дополнительные ограничения а^kх ≤ β^k, связанные с правильными отсечениями, используются только как средство отсечения не целочисленного решения и перехода от k-го этапа к (k + 1)-му этапу. Сами ограничения нас как бы не интересуют, так как их влияние учтено через введение новых базисных переменных.

Очевидно, что в методе Гомори можно выделить большие итерации, которые начинаются с введения дополнительного ограничения (18-63), и малые итерации симплекс-метода для решения задачи линейного программирования с этим ограничением.

Пример 18-3. Решим с помощью алгоритма Гомори следующий численный пример:

Введением неотрицательных целочисленных переменных х₃ и x₄ каноническая форма рассматриваемой системы приобретает вид:

Соответствующая j-задача будет определяться следующим образом:

1. Опорный план
   х^исх = {0, 0, 0, 38, 2}.
2. Номера базисных переменных
   N_б^исх = {3, 4}.
3. Номера не базисных переменных
   N^исх= Q - N^исх_б = {1, 2}.
   Не базисные переменные выразим через базисные по формуле (18-66):
   х₃ = 38 - 2x₁ - 9x₂;
   х₄ = 2 - х ₁ + 2х₂.

Для получения лексикографической симплекс-таблицы исходного j-псевдоплана введем новую переменную

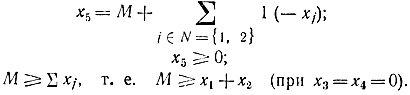
Решая систему уравнений, с учетом целочисленности переменных х₁ и х₂ имеем строгое неравенство

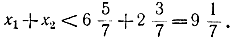
Следовательно,

Лексикографически правильная симплексная таблица 18-1 [T^исх(0)] имеет вид:

где x^исх(0) - коэффициенты в правых частях уравнений; Q₀ = {0, 1, 2, 3, 4, 5} - расширенное множество индексов переменных; N₀ = {0, 1, 2} - расширенное множество индексов не базисных переменных; N_б = {3, 4, 5} - номера базисных переменных.

Таблица 18-1

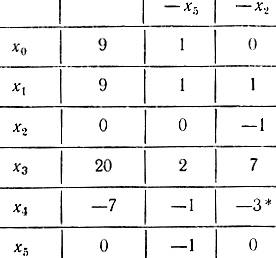
Таблица 18-2

Найдем переменную, выводимую и вводимую в базис, по правилам (18-62) и (18-17) соответственно. Направляющим элементом, помеченным в табл. (18-1) звездочкой, является

Переменная x₁ выводится из базиса, вводимой в базис переменной является х₅. Элементы симплекс-таблицы при этом преобразуются по следующим соотношениям:

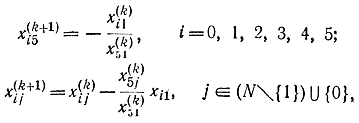
где знак " \ " означает вычитание множеств. В результате преобразований, соответствующих двойственному циклу, l-нормальная таблица приобретает вид табл. 18-2 [Т^исх(1)]

В соответствии с первым шагом алгоритма Гомори решаем l-задачу, состоящую в проверке условия допустимости, нахождении переменной, выводимой из базиса, переменной, вводимой в базис, и пересчете таблицы, аналогично предыдущим преобразованиям. При этом k* = 4, l* = 2, направляющим элементом таблицы является х₄₂ = -3, а индекс j принимает значения

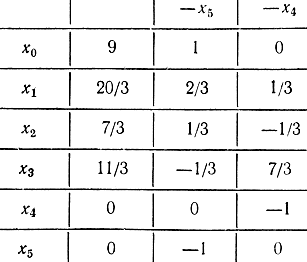
Таблица 18-3

В результате этого двойственного цикла, когда новая переменная вводится в базис, приходим к исходной j-задаче, данные которой отражены в табл. 18-3.

Максимизация расширенного плана (l-задача) имеет вид:

1. l-псевдоплан
   х^исх={x₀, x₁, x₂, x₃, x₄, x₅} = {9, 20/3, 7/3, 11/3, 0, 0};
2. номера базисных переменных
   N_б^исх(2) = {j, 2, 3};
3. номера не базисных переменных
   N^исх(2)(N\{l}) ≚{k} = {4, 5},
   N^иcx(2) = {0, 4, 5}.

Для табл. 18-3 повторяем общую итерацию l-метода; l-псевдоплан удовлетворяет условию допустимости и, следовательно, является l-оптимальным планом. В соответствии с алгоритмом Гомори переходим ко второму и последующим шагам.

Второй шаг. Проверяем, является ли l-оптимальный план целочисленным. План не целочислен, переходим к третьему Шагу.

Третий шаг. Полагаем k = 0 (нулевая большая итерация).

Четвертый шаг. Выбираем наименьшую по номеру строку табл. 18-3, которой соответствует не целочисленная компонента

Пятый шаг. Строим правильное отсечение:

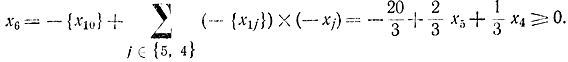
Шестой шаг. Приписываем строку, соответствующую новому ограничению, к таблице T⁰ (табл. 18-3) и получаем таблицу Т⁰ (табл. 18-4). Формирование нового ограничения и переход к решению очередной l-задачи отражает прямой цикл алгоритма.

Седьмой шаг. К l-задаче, записанной в виде l-нормальной таблицы Т⁰, применяем l-метод и производим описанные ранее процедуры.

Результаты последующих преобразований отражены в табл. 18-5, табл. 18-6, табл. 18-7. l/-оптимальный план является целочисленным; таким образом, получаем максимум линейной формы z = 8 при х₁ = 6 и х₂ = 2.

Геометрическая иллюстрация решения целочисленной задачи дана на рис. 18-6. Пунктиром показаны прямые, осуществляющие правильные отсечения.

Следует заметить, что практика решения задач с помощью первого алгоритма Гомори показывает практически малую его эффективность из-за большого количества требуемых итераций.

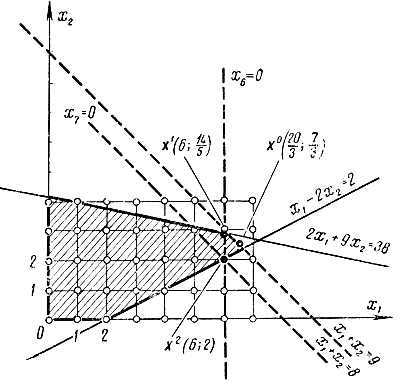
Рис. 18-6. Пояснение к примеру 18-3

Так, в задачах, в которых без требования целочисленности было необходимо 20 итераций, для получения решения в соответствии с первым алгоритмом Гомори для целочисленной задачи даже 2 000 итераций еще не дали сходимости [Л. 89]. Поэтому на практике очень часто используют другие алгоритмы решения линейных задач целочисленного программирования, основанные на некоторых эвристических принципах, используемых для построения отсечения. Хотя сходимость этих алгоритмов в общем случае не доказана, они очень часто обеспечивают достаточно быструю сходимость.

Таблица 18-4

Таблица 18-5

Таблица 18-6

Таблица 18-7

Так, в отличие от алгоритма Гомори дополнительную отсекающую . плоскость (18-51) можно выбирать так, чтобы она пересекала ось x_j (j ∈ N) в точках, как можно более удаленных от начала координат. При этом переменные x_j, удовлетворяющие уравнению (18-51), будут принимать максимальные значения, что соответствует наибольшему продвижению в область допустимых решений от точки х = || х₀, 0 ||. В соответствии с этой идеей выбирается такая переменная, для которой отношение {x_l0}/{x_lj} имеет максимальное значение. Другая идея основана на одновременном построении всех сечений, соответствующих не целочисленным переменным, и включении их в расширенную задачу. Число отрицательных переменных в этой задаче будет равно числу дополнительных ограничений.

В случае применения ЦВМ при решении задач целочисленного программирования возникают дополнительные трудности, связанные с проблемой округления. Дело в том, что решение, вычисленное ЦВМ, может быть в результате округлений не целочисленным.