а) Решение задач целочисленного программирования с помощью динамического программирования.

Динамическое программирование является универсальным методом отыскания глобального экстремума любых задач, для которых справедлив принцип оптимальности. В' последних трех главах изложение подчинялось по задачной ориентации, но, естественно, что по методийная линия, использованная в первых главах "Методов оптимизации", с успехом может быть применена и для решения задач целочисленного программирования. Принцип оптимальности Веллмана заведомо применим к сепарабельным и линейным функциям цели (см. гл. 14).

Ограничения в виде неравенств и целочисленности учитываются в рекуррентном процессе решения функционального уравнения Веллмана, так же как в решении транспортной задачи.

Для случая сепарабельной функции цели можно составить общую вычислительную схему решения задачи нелинейного целочисленного программирования по методу динамического программирования [Л. 89]. Причем размерность задачи динамического программирования определяется характером функции цели и огранлчений. В этом можно убедиться на примере транспортной задачи, рассмотренной в гл. 15.

Основная трудность при использовании метода динамического программирования заключается в сведении исходной задачи к модели многоэтапного процесса оптимизации, используемого в этом методе, с введением функции Беллмана. В каждой конкретной задаче при этом используются свои приемы, комплексом которых можно овладеть после известного опыта.

На примере задачи об опасной переправе рассмотрим применение этого метода. Группа, состоящая из m миссионеров и l людоедов, должна переправиться через реку на лодке, которая имеет ограниченную грузоподъемность К [Л. 80]. Лодка управляется одним или более пассажирами в любой комбинации. На каждом берегу и в лодке должно соблюдаться условие не людоедства, заключающееся в том, чтобы число людоедов в группе не превышало числа миссионеров (m,l).

Обозначим число миссионеров и людоедов на левом берегу через m₁ и l₁ на правом берегу m₂ и l₂ и в лодке m и l. Соответственно сформулируем более общие условия не людоедства:

Составим функциональное уравнение Беллмана, для чего введем функцию S_N (m₂, l₂), равную максимальному числу людей на правом берегу после N шагов при условии, что процесс перевозки начинался с m₁ миссионеров и людоедов на левом берегу и m₂ и l₂ на правом берегу. Считается, что на любом шаге ни один человек не возвращается на первый берег со второго, если все уже находятся на втором берегу.

Один шаг заключается в перевозке x₁ миссионеров и y₁ людоедов с левого на правый берег и в обратной перевозке х₂ миссионеров и y₂ людоедов с правого на левый берег.

В соответствии с принципом оптимальности для N ≥ 2 можно написать:

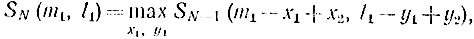
где величины х₁, y₁, х₂, y₂должны удовлетворять следующим условиям:

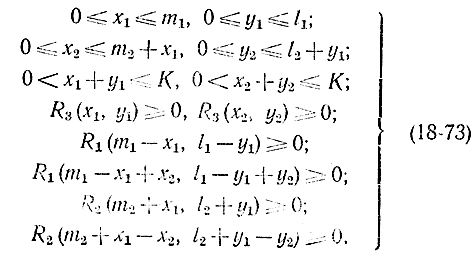
Для N = 1 имеем:

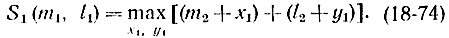
Минимальное число перевозок равно такому N, для которого

Пример 18-4. Допустим, что суммарное количество миссионеров m₁ + m₂ = 3 и суммарное количество людоедов l₁ + l₂ = 3, грузоподъемность лодки К = 2.

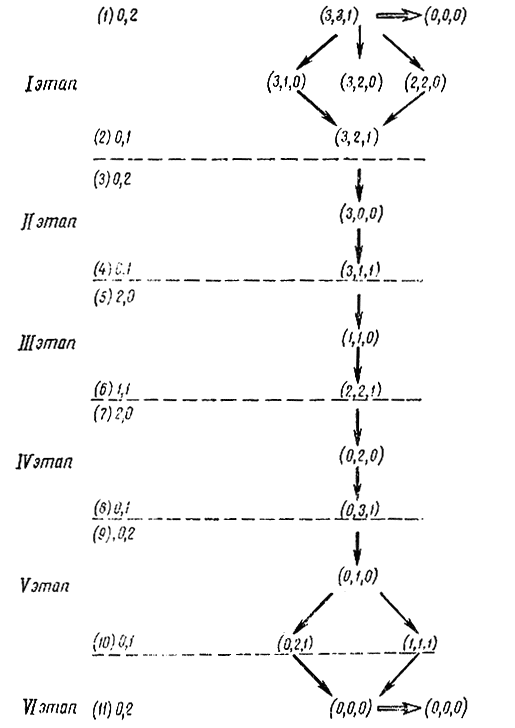
Рис. 18-7. Пояснение к примеру 18-4

Обозначим через (i, j) состояние, при котором i миссионеров и j людоедов находятся на левом берегу, а 3 - i и 3 - j - на правом берегу Тогда с точки зрения не людоедства допустимы только следующие состояния: (0,1), (1, 1), (3, 1), (0, 2), (2, 2), (3, 2), (0, 3), (3,3). Используя функциональное уравнение, получаем: S₁ (0,1) = 6; S₁(1 ,1)= 6; S₁ (3, 1) = 2; S₁ (0, 2) = 6; (2, 2) = 3; S₁ (3, 2) = 2; S₁ (0, 3) = 4; S₁ (3, 3) = 1.

Нетрудно убедиться, что если

Учитывая это обстоятельство, с помощью рекуррентных функциональных уравнений получаем:

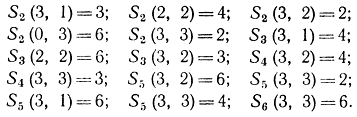
Отсюда следует, что минимально требуемое число перевозок равно шести.

Процедуру решения рассмотренной задачи легко проследить с помощью графа, представленного на рис. 18-7. Каждое ребро графа соответствует перевозке с одного берега на другой. Таким образом, одному этапу динамического программирования соответствуют два ребра графа. Стрелки указывают направление действия. Цифры в скобках около каждой вершины означают: первая - число миссионеров, вторая - число людоедов на одном из берегов, последняя цифра обозначает левый (1) и правый (0) берега; две цифры слева соответствуют числу перевозимых миссионеров и людоедов.

Таким образом, процедура направленного поиска оптимального решения заключается в следующем:

1) перевозим двух людоедов с левого берега на правый;

2) возвращаем одного людоеда назад на левый берег;

6) перевозим одного миссионера и одного людоеда с правого на левый берег;

11) перевозим двух людоедов с левого берега на правый.

Соответствующие значения функции Беллмана на каждом этапе будут следующие:

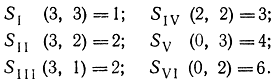
Из рис. 18-7 видно, что в проблеме миссионеров и людоедов существует более одного оптимального пути решения. Так, на первом этапе можно или перевезти двух

людоедов и затем одного людоеда обратно или одного миссионера и одного людоеда, а потом одного миссионера обратно. Число перевозок и шагов поиска решения будет одинаковым.