б) Метод ветвей и границ

Комплексный подход по схеме ветвлений объединяет целый ряд близких комбинаторных методов, как-то: метод ветвей и границ, метод последовательного конструирования, анализа и отсева вариантов и др. Общая идея метода крайне проста. Множество допустимых планов некоторым способом разбивается на подмножество. В свою очередь каждое из подмножеств по этому же или другому способу снова разбиваются на подмножества до тех пор, пока каждое подмножество не будет представлять собой точку в многомерном пространстве. В силу конечности наборов значений переменных дерево подмножеств (схема ветвлений) конечно.

Построение схемы ветвления есть не что иное, как формирование процедуры перебора. Перебор может осуществляться различными способами. Сечение исходной допустимой области G₀ гиперплоскостью на части G₁₁ и G₁₂. С последующим разделением G₁₁ на G₂₁ и G₂₂ (рис. 18-8) представляет собой построение дерева ветвлений с соответствующими подмножествами, как это показано на рис. 18-9.

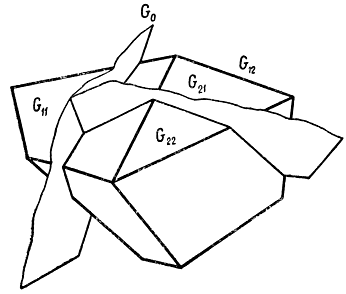
Рис. 18-8. Пояснение к методу ветвей и границ

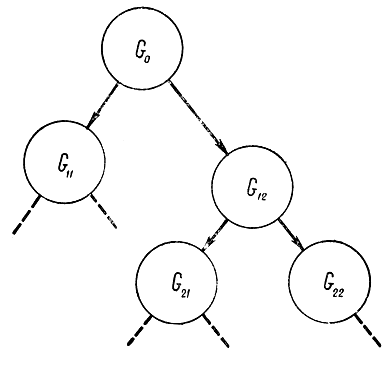
Рис. 1809. Граф решения для метода ветвей и границ

Возможность оценки образуемых подмножеств по наибольшему (наименьшему) значению для задач максимизации (минимизации) позволяет сократить перебор в силу того, что одно из подмножеств при выполнении определенных соотношений исключается и не нуждается в последующем анализе.

Понятно, что выбор оценок и схемы ветвления взаимосвязаны и трудно указать общие рекомендации по использованию на практике этого метода.

Схема ветвления иллюстрируется решением обобщенной задачи одномерного раскроя (пример 18-5) с конкретными числовыми данными.

Пример 18-5. Имеются заготовки длиной я₁ = 18, а₂ = 16, а₃ = 13. Разрезая их на части, но не склеивая, можно получать детали длиной b₁ = 12, b₂ = 10, b₃ = 8, b₄ = 6, b₅ = 5, b₆ = 4. Стоимость каждой детали известна и в условных единицах численно равна их длине. Перечисленные детали представляют собой "портфель заказов", который желательно обеспечить в первую очередь. В том случае, если это невозможно, максимизируется стоимость получаемых деталей из заданной номенклатуры. Если же портфель заказов обеспечивается, необходимо максимизировать стоимость дополнительной продукции.

Величину 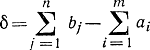будем называть дефицитом. Отрицательность дефицита еще не означает существование варианта раскроя, при положительном дефиците раскрой невозможен. Это свойство может быть использовано для указания перспективности варианта. Так, если заготовка а₂ раскраивается на b₃ и b₅, то независимо от комбинаций остальных отрезков раскрой невыполним, поскольку для оставшихся отрезков дефицит положителен.

Первые этапы приводимой ниже схемы ветвления, использующей комбинаторные отношения подмножеств вариантов, показаны на рис. 18-10. На первом этапе формируются разбиения первой группы отрезков (заготовок) на вторую группу (деталей) независимо от того, какой именно отрезок первой группы разрезается. Количество ветвей первого этапа можно вычислить лишь по рекуррентным соотношениям. Смысл подмножества {1, 2, 3} заключается в том, что один из отрезков первой группы в результате раскроя дает один отрезок второй группы, один из оставшихся отрезков первой группы раскраивается на два отрезка второй группы из числа оставшихся и, наконец, последний отрезок первой группы делится на три части, образуя три отрезка второй группы. На втором этапе формируются все перестановки (с учетом порядка) элементов первого этапа. Скажем, вариант {2, 1, 3} означает, что именно первый элемент первой группы аг разрезается на две части и т. д.

Очередной этап ветвления образуется фиксацией отрезков второй группы при" указанном на предыдущем этапе числе частей, на которое разрезается первый элемент. Другими словамй, формируем сочетания по числу разделений первого элемента первого множества на число элементов второго множества. В дальнейшем фиксируем отрезки второй группы при втором элементе первой группы и, наконец, при оставшемся элементе первой группы получаем конкретные варианты раскроя, всего 447 вариантов. В подробно описанной схеме ветвления в отличие от часто применяемых ни на одном этапе не используется конкретный числовой материал. Рекомендуется построить для этого же примера иную схему ветвления, начиная с третьего этапа, по следующему признаку: отрезки второй группы фиксируются при элементе первой группы, разрезаемом на меньшее число частей. Затем надо сравнить схемы. Нетрудно убедиться, что на каждом этапе ветвление осуществляется по регулярной процедуре, что позволяет запоминать лишь один вариант. Сравнение дефицитов предыдущего и последующего вариантов позволяет выделить перспективный и соответствующую ему ветвь. Окончательный результат имеет вид:

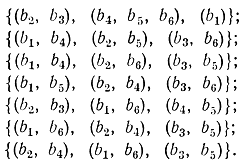
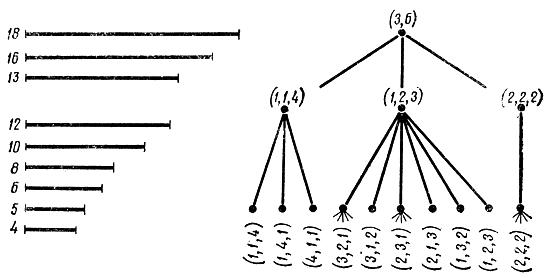
Рис. 18-10. Пояснение к примеру 18-5

Формально задачу можно было бы свести к общему виду линейной задачи целочисленного программирования, но такое сведение приведет к значительному увеличению количества переменных и другим трудностям. Матрица коэффициентов при этом приобретает квадратичный вид с неплотным заполнением ее отличными от нуля элементами. Как правило, задачи многоиндексные с большим числом условий и сложной упорядоченностью рекомендуется решать по схеме ветвлений, используя специфику условий и ограничений.

Для задач дискретного типа этот метод получил наибольшее распространение в силу простоты и доступности самого метода и, кроме того, наиболее естественной формы описания систем условий и ограничений, являющихся, как правило, отправным пунктом построения дерева ветвления. По существу большинство оригинальных алгоритмов (Балаша - Фора - Мальгранжа, Черенина, Джеффриона, Хиллиера и др.) являются модификациями метода ветвей и границ с учетом специфики условий задачи [Л. 97].