18-6. Другие методы оптимизации

Сюда относятся прежде всего приближенные методы решения задач целочисленного программирования, не гарантирующие сходимости за конечное число шагов, а также вероятностные методы, обеспечивающие сходимость в вероятностном смысле. Сюда же относятся эвристические методы в чистом виде и в комбинации с вероятностными. Упоминавшиеся ранее человеко-машинные методы оптимизации следует отнести также к этой группе. Кроме того, здесь же рассматриваются новые методы решения типа лингвистических, близкие к человеко-машинным.

Решение задач целочисленного программирования с помощью лингвистических моделей. Специфические свойства лингвистических методов позволяют эффективно их использовать при разработке систем управления большими системами. К таким свойствам в первую очередь отнесем простоту общения человека с машиной, так как лингвистические методы используют в качестве входных языки, более понятные неспециалисту, чем известные алгоритмические языки, а также автоматизированный (в режиме диалога) процесс формирования модели решения задачи.

Проследим основные моменты метода лингвистического моделирования на решении задачи об опасной переправе [Л. 15]. Обозначим присутствие миссионера символом m присутствие людоеда символом l. Тогда цепочка символов (которую в дальнейшем будем понимать как фразу языка описания состояний управляемой системы) mmmmllll будет описанием начального состояния на левом берегу. При этом способе описания состояний каждая перевозка соответствует правилу вида α → ε, где α - цепочка из символов m и (или) l, а ε - пустой символ. Отметим, что длина цепочки α не должна превышать грузоподъемность лодки, а количество символов m не должно быть меньше числа символов l (условие не людоедства в лодке). Так, для случая, когда на левом берегу 4 миссионера и 3 людоеда, имеет место состояние mmmmlll. Пусть мы хотим перевезти двух миссионеров и одного людоеда, тогда правило выглядит как подстановка mml→ε в, применение которой к описанию состояния дает 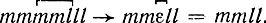. Введем в рассмотрение двойные перевозки, т. е. предположим, что лодка совершает рейс с левого берега на правый и обратно. Такие перевозки запишутся как правила вида α → β, где α и β - непустые цепочки, по длине не превышающие величины грузоподъемности лодки, и, кроме того, в них соблюдаются условия не людоедства. Если состояние на левом берегу имеет описание mmmmlll и мы перевозим с левого берега на правый двух миссионеров и одного людоеда, а обратно одного миссионера и одного людоеда, то правило приобретает вид: mml → ml, а результат его применения - 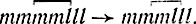. Таким образом, мы сформировали знакомую модель задачи, содержащую S-язык описания состояний, который определяется как подмножество множества 2 всех цепочек, составленных из символов m и l, и множество правил преобразования, каждое из которых имеет вид α→β, где α,β ∈Σ, a Σ - алфавит, состоящий из символов m и l.

Построенная модель не дает еще ничего нового. В самом деле, она представляет собой просто удобную запись порождения графа управления - ориентированного графа, вершины которого отождествлены с состояниями на левом берегу, а ребра - с двойными перевозками (см. рис. 18-7). Эта модель не дает никаких сведений о том, какую перевозку из нескольких возможных для каждого состояния следует применить, чтобы общее число перевозок было минимальным. Заметим, что метод динамического программирования имеет дело практически с тем же самым описанием.

Основная особенность методов лингвистического моделирования заключается в том, что они вводят некие макроописания задачи, которые позволяют объединять сходные по структуре описаний состояния в макросостояния. Этим достигается рассмотрение задачи с более общей точки зрения, т. е. решение ищется не на графе, а на макрографе управления, имеющем гораздо меньше вершин и ребер.

Построение макросостояний осуществляется при помощи специального аппарата порождающих грамматик, разработанного Н. С. Хомским [Л. 98] в целях моделирования естественных языков. Порождающая грамматика Г представляется как совокупность терминального словаря Г, нетерминального словаря N, Т ∩ N = ∅, начального символа S∈N и множества правил вывода Р, имеющих вид α→β, где в простейшем случае α ∈ N, β∈(N ∪ Т) - цепочка, составленная из символов терминального и нетерминального словарей.

Существуют специальные методы построения грамматик поданному подмножеству фраз языка. Эти методы в некоторых случаях допускают автоматическое построение грамматики [Л. 99], но в большинстве случаев оказывается возможным автоматизированное (в режиме диалога) построение.

В случае задачи об опасной переправе удается осуществить автоматическое построение грамматик, в результате которого получаются три грамматики, разбивающие все множество состояний на три подмножества, соответствующие условиям нелюдоедства.

Пример 18-6. Дадим решение задачи о людоедах и миссионерах для конкретного случая 4 миссионеров (М = 4) и 4 людоедов (L = 4) на левом берегу. Условия нелюдоедства в данном случае имеют вид: M≥L, М = 0.

Каждая из упомянутых грамматик соответствует одному из макросостояний управляемой системы. Формальная запись в данном случае выглядит следующим

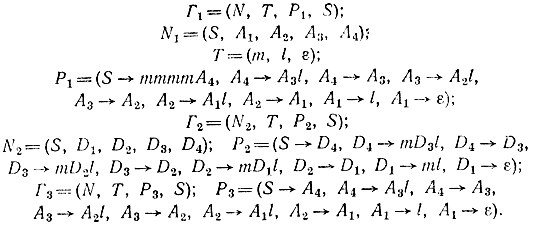
Каждая из этих грамматик может использоваться для описания как порождения состояний из соответствующего макросостояния, так и для отнесения произвольного состояния к одному из макросостояний, соответствующих основным условиям не людоедства.

Следующий этап построения решения заключается в формировании так называемых макродействий, которые представляют собой обобщенные правила передвижения как между состояниями, принадлежащими одному макросостоянию, так и различным макросостояниям. Поскольку в любой цепочке (фразе) языка вместо какой- либо ее подцепочки можно подставить цепочку того же типа (выводимую из того же нетерминального символа) и полученная фраза будет принадлежать языку, то будем рассматривать изъятие подцепочки из описания состояния на левом берегу как перевозку с левого берега на правый, а подстановку цепочки того же типа как перевозку в обратном направлении. При этом однотипные цепочки должны быть непустыми, так как лодка может двигаться только с людьми на борту, и по величине не превышающими величины грузоподъемности. Пусть Φ (X) - множество цепочек типа X (выводимых из нетерминального символа X). Тогда обозначим через Φ* (X) множество цепочек типа X, удовлетворяющих введенным ограничениям. В этом случае правила перехода внутри макросостояний могут быть записаны в виде

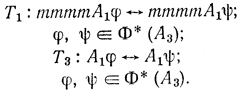
Переходы между элементами макросостояния, соответствующего Г₂ невозможны, так как для любого i, 1≤i≤, Φ*(D) содержит только одну цепочку ml.

Переходы между состояниями, принадлежащими различным макросостояниям, могут быть представлены в виде

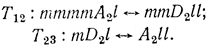
Итак, теперь построен макрограф управления, содержащий три вершины S₁ S₂, S₃, соответствующие макросостояниям, и ребра, соответствующие макродействиям.

Построением макрографа заканчивается формирование семиотической модели решения задачи. Пусть начальное состояние имеет описание γ₀ = mmmmlll, а конечное γ_n = ε. Нетрудно убедиться, что γ₀ ∈L (Γ₁) или γ₀ ∈ L (Γ₂) (т. е. 70 может быть порождена грамматиками или Γ₂) а γ_n ∈ L (Γ₂) или γ_n ∈ L (Γ₃). Поскольку γ₀≠γ_n и переход между элементами макросостояния S₂ невозможен, то считаем, что γ₀ ∈ L (Γ₁), γ_n ∈ L (Γ₃). В этом случае общая запись решения может быть представлена в терминах макродействий как последовательность Т₁, Т₁₂, Т₂₃, Т₃. Для того чтобы было возможно

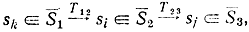
приравняем правую часть Т₁₂ к левой T₂₃, т. е.

Это равенство будет выполнятся, если в макродействии T₁₂ применить правило D₂→D₁ а в T₂₃→D₂→mD₁l. Тогда переход из S₁ в S₂ имеет вид:

Применив к полученному выражению те или иные правила грамматик Γ₁, Γ₂, Γ₃ можно получить все возможные переходы из S₁ в S₃.

Для построения пути в S₁ подставим в Т₁ цепочки типа А₃. В соответствии с Φ* (А₃) = {lll, ll, l} число возможных переходов ограничено. Применив правило А₁ → l или А₁ →ε, можно получить, что из начального состояния за одну транспортировку лодки достижимы состояния с описаниями mmmmlll и mmmmll, а за две - mmmml.

При построении пути в S₃ учтем тот факт, что при последней транспортировке лодка остается на правом берегу, т. е. если в левой части выражения для Т₃ длина цепочки не превышает величины грузоподъемности, то возможно оператора A₁φ→ε. Применив правило А₁ →l или А₁→ ε, получим, что конечное состояние достижимо за один переход из состояний с описаниями lll, ll, l и за два перехода из состояний llll.

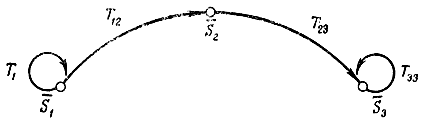
Рис. 18-11. Возможные переходы между элементами для примера 18-6

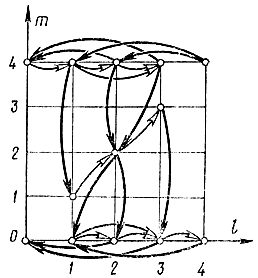
Рис. 18-12. Возможные пути из начального а коночное состояния для примера 18-6

Объединяя пути в S₁ и S₃ и переходы S₁ → S₂ → S₃, получаем возможные решения, порождаемые из последовательности макродействий T₁, Т₁₂, Т₂₃, Т₃ (рис. 18-11). Отметим, что каждый из этих путей имеет минимальную для данных условий задачи длину. Отметим также, что здесь предполагается возможность осуществления параллельного вывода, в случае же последовательного вывода каждый из путей, показанных на рис. 18-12, был бы получен поочередно.