Глава 1. Цели и средства в анализе образов

1.1. Цели анализа образов

Основными понятиями теории образов являются объекты и отношения. Объектами в теории образов служат образующие, конфигурации, идеальные и деформированные изображения, классы образов. Отношения в теории образов задаются в виде преобразований подобия, комбинаторных отношений, правил идентификации и механизмов деформации.

Объекты распределены по уровням, причем образующие занимают нижний уровень, конфигурации ближайший к нему верхний и т. д. В иерархической системе образов может содержаться значительное число уровней.

При синтезе образов продвижение происходит от нижнего к верхнему уровню системы. Анализ образов представляет собой обратный процесс: в качестве отправной точки анализа выбирается верхний уровень образа и предпринимается попытка расчленить объект-образ на объекты, принадлежащие низшим уровням.

Было бы бессмысленно говорить в такой постановке об анализе прежде, чем определен процесс синтеза. В первом томе мы убедились, что теория обладает высокой степенью гибкости; это было показано на значительном числе частных случаев, количество которых будет существенно увеличено в данном, а также третьем томах. Это означает, естественно, что анализ образов может принимать самые различные формы в зависимости от конкретной природы образующих, типа соединения и тому подобных факторов. На данной стадии достаточно остановиться на наиболее распространенных разновидностях анализа, с другими же мы будем встречаться по мере нашего продвижения вперед.

В анализе образов нам придется изучать отображения между различными пространствами, встречающимися в теории образов: пространством конфигураций, алгеброй изображений, алгеброй деформированных изображений, структурой класса образов. Точно такая же ситуация существует в классических алгебраических системах, в которых мы изучаем, например, отображения между группами. Мы изучаем, в частности, отображения, сохраняющие алгебраические свойства, гомоморфизмы, или другие свойства инвариантности и/или ковариантности.

Случай 1.1.1. (восстановление изображений). Данная задача состоит в отыскании отображения из алгебры деформированных изображений 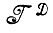в алгебру идеальных изображений 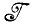. Предполагается, что отображение 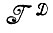→ 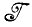восстанавливает идеальное изображение I, которое в результате воздействия механизма деформации D было превращено в наблюдаемый объект I^D.

В разд. 1.1.3 мы обсудим, что именно понимается под восстановлением идеального изображения I.

Напомним в качестве соответствующего примера задачу отыскания образа-множества, преобразованного в результате воздействия пуассоновского механизма деформации к наблюдаемому точечному образу (см. т. 1, случай 4.5.2).

В этом случае, так же как и в последующих, нет оснований полагать, что ответ будет однозначным. Если это так, то мы сталкиваемся с необычной, вырожденной ситуацией. В противном случае мы попытаемся выбрать отображение, которого было бы естественным, обоснованным или даже оптимальным в некотором точном смысле.

Иногда требуется, чтобы восстановление изображения сопровождалось определением примененного механизма деформации. Тогда нас интересует отображение 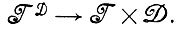. Такая постановка имеет смысл в тех случаях, когда механизм деформации представляет интерес для исследователя как таковой или он хочет узнать о структуре механизма деформации D больше того, что было задано ему априори: например, какая вероятностная мера действует на множестве деформаций.

Случай 1.1.2 (анализ изображения). Для заданного изображения I следует отыскать конфигурацию с, порождающую I. Эта задача включает определение образующих и комбинаторных отношений конфигурации с, так что искомое отображение имеет в 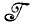→ 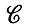(R).

В случае временных образов типа процессов, например, приходится решать задачу сегментации, а также отыскивать виды сигналов, соответствующие отдельным отрезкам на временной оси (см. т. 1, случай 3.4.3).

Случай 1.1.3 (аппроксимация изображения). Располагая обычными исходными данными и алгеброй изображений 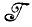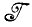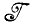^*, ⊂^*, необходимо найти "хорошее" отображение, такое, что получаемое изображение 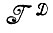→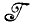^* близко в некотором смысле к изображению I∈.

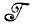В этом случае алгебра идеальных изображений расширяется до алгебры 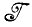^* и делается попытка получить наилучшую аппроксимацию изображения I, используя элементы алгебры 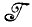^* и информацию, содержащуюся в наблюдаемом изображении I^D= dl.

Если, например, 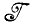- алгебра изображений, состоящая из выпуклых множеств (см. т. 1, случай 3.5.9) и 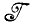^* - алгебра борелевских множеств, тогда типичная задача аппроксимации изображения будет заключаться в отыскании элемента алгебры 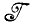^* для наблюдаемого изображения, полученного I∈ 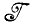из пуассоновекой деформацией.

Случай 1.1.4 (распознавание образов). Для заданного изображения I^D требуется найти класс образов P_r, к которому принадлежит идеальное изображение I,I^D=dI, I∈P_r.

Пусть, например, алгебра образована движениями, как в случае 3.7.1 из первого тома, и группа преобразований подобия 5 есть прямое произведение евклидовых движений пространства и переносов оси времени. Пусть каждый класс образов Р_r образован из некоторого прототипа (см. т. 1, разд. 3.1), к которому применена группа преобразований подобия S. Отыскание прототипа, лежащего в основе наблюдаемого образа движения I^D, и представляет собой задачу распознавания образов.

В случае 1.1.3 мы расширили множеств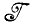о до 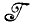^*. Идея, заложенная в основу этой операции, естественно, заключается в том, что исходная алгебра изображений была слишком ограниченна и мы были вынуждены расширить ее. С другой стороны, может оказаться, что алгебра 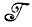или 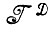слишком велика, содержит много информации, часть которой или не имеет отношения к делу, или представляет слабый интерес. Тогда вводится разбиение 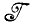_* алгебры 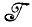(или 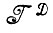- может встретиться и такой случай), и идеальное изображение I представляется с помощью соответствующим образом выбранного элемента разбиения 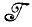_*. Его можно рассматривать как (частичное) описание идеального изображения I (или деформированного изображения I^D).

Случай 1.1.5 (описание изображения). При заданных алгебрах 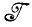и 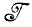_*, требуется найти отображение f: 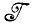→ 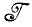_*, такое, что изображение I∈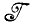_* хорошо представляет идеальное изображение I.

Если, например, алгебра 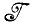состоит из образов-соответствий с действительными значениями соответствий и образует бесконечномерное функциональное пространство, то можно попробовать использовать разбиение 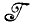_*, параметризованное с помощью конечного числа действительных параметров, и выбрать параметризацию и отображение f такими, что при замене идеального изображения I изображением I_* теряется незначительное количество информации.

Для получения хорошего описания изображения необходимо не только хорошо подобрать элементы разбиения, но и тщательно произвести выбор разбиения _*.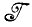

Способ осуществления этого выбора зависит от цели описания изображения. Один вариант связан с запоминанием данных, когда целью является сжатие данных. Другой вариант относится к передаче данных, когда при определении существенных с точки зрения задачи кодирования обстоятельств следует учитывать также и канал связи.

Случай 1.1.6 (вывод и абдукция образов). При заданных элементах алгебры 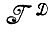следует выполнить выводы, касающиеся алгебры 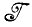и лежащей в ее основе структуры регулярности. Эта процедура может включать определение образующих, типа соединения, правила идентификации и т. д.

Когда обрабатываются структуры образов в целом, а не просто отдельные изображения, процессор образов представляет собой иногда сложную систему, которая сама по себе обладает структурами образов, как в гл. 6. Их связь с рассматриваемой теорией структуры имеет в этом случае решающее значение.

Существуют и другие виды анализа образов, заслуживающие упоминания и встречающиеся в последующих главах. Может оказаться, что алгебра 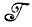известна нам, за исключением некоторых деталей; при этом требуется определить структурные параметры алгебры изображений, например найти признаки образующих. Может возникнуть и необходимость определить вероятностные меры на множестве регулярных конфигураций 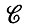(R) и алгебре идеальных изображений 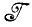(см. т. 1, гл. 2 и 3) или даже вероятностные свойства деформаций.

Как бы то ни было, допустим что задана система образов и необходимо провести один из упоминавшихся выше видов анализа образов как следует его выполнять? В столь общем виде этот вопрос оказывается почти бессмысленным и, лишь обратившись к конкретной и в определенной степени детализированной системе образов, можно приступать к выбору специфических методов решения, как и будет сделано в последующих главах.

После того как мы рассмотрим некоторые случаи, станет очевидным, что основным препятствием можно считать наличие деформаций, уничтожающих информацию. Если бы нам приходилось иметь дело только с алгеброй идеальных изображений, некоторые задачи анализа были бы сняты, например восстановление изображения, а остальные оказались бы несложными (по крайней мере, в принципе).

Обратимся, скажем, к распознаванию рукописного текста. Этой задаче уделялось много внимания, однако полученные результаты не очень впечатляют. Если бы мы имели дело лишь со стилизованным письмом, скажем с написанными раздельно символами специального алфавита, то процесс распознавания действительно можно было бы организовать алгоритмически. В этой связи следует отметить основополагающую работу Идена (1961).

Если же, с другой стороны, текст не расчленен и допускаются индивидуальные вариации почерка, то приемлемое решение задачи распознавания кажется все еще отдаленным, несмотря на все предпринимавшиеся попытки.

Можно было бы привести другие примеры. Аналогичное положение наблюдается в области автоматического распознавания речи (см., например, монографию Фланагана (1972)). Многократно было продемонстрировано, что можно синтезировать речь, обеспечивая ее высокое качество. Обратная задача настолько труднее, что специалисты в этой области высказывались пессимистически относительно возможностей получения реальных решений для реальной речевой среды. И снова причина, по-видимому, заключается в чудовищной изменчивости и сложных взаимозависимостях, порожденных соответствующими механизмами деформации.

Мы знаем, что в обоих этих случаях распознавания можно добиться, поскольку мы, будучи людьми, постоянно проводим такое распознавание, хотя нам в точности не известно, как мы это делаем.

Учитывая возмущающее влияние деформаций, заманчиво организовать анализ образов в два этапа. В первую очередь следует попробовать скомпенсировать влияние деформаций с помощью какой-нибудь предварительной обработки: подавления шумов, фильтрации, сглаживания или иных процедур очищения. Затем следует приступить к анализу как таковому, используя представленные в структурированном виде очищенные данные. Можно надеяться, что таким способом задача будет сведена к поддающемуся решению виду.

Литература, посвященная распознаванию образов, изобилует описаниями подобных попыток. Часто процедура очищения заимствуется из теории связи или традиционных методов статистического вывода и модифицируется применительно к особенностям решаемой задачи. Иногда при модификации предпринимается попытка учесть наиболее общие и качественные свойства образов. На этом пути были получены полезные результаты, особенно в тех случаях, когда изменчивость деформаций ограничена.

Успешность подобного подхода зависит от выбора способа предварительной обработки. Частные методы выбора могут оказаться полезными, однако мы считаем, что в принципе при проведении анализа образов должна использоваться структура образа в целом и этот анализ должен основываться непосредственно на соответствующей цепи синтеза образов, включая деформации .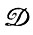

С другой стороны, необходимо принимать во внимание вычислительные ограничения и стремиться к построению алгоритмов, которые действительно могут быть реализованы при разумных затратах вычислительных ресурсов. В практическом отношении наша ситуация несколько напоминает положение, сложившееся в теории информации. Общие теоремы теории информации не всегда указывают такие оптимальные схемы кодирования, которые можно бы было практически использовать. Они определяют, однако, нижние грани, указывающие теоретически достижимое, и это помогает при оценке качества конкретных кодов. Точно так же в анализе образов результаты, связанные с оптимальностью, могут не иметь непосредственного применения, но они помогают нам при разработке хороших, если не оптимальных, процедур анализа и указывают, сколь далеки мы от теоретически возможного оптимума.

Итак, при рассмотрении в последующих главах каждой задачи анализа образов мы будем начинать с определения полной цепи синтеза, основываясь либо на результатах, полученных в первом томе, либо вводя аналогичными способами новые структуры образов.

При таком подходе нам не всегда удается определить структуру образов во всех подробностях. Скорее наоборот часто мы будем вынуждены примириться с тем, что некоторые характеристики образа невозможно полностью определить априори.

Подобное отсутствие полной определенности часто возникает на последнем этапе в связи с деформациями 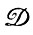, где обычно мы сталкиваемся с параметрами, которые априори не известны и должны устанавливаться эмпирически. Не так часто, но и не как исключение при анализе возникает ситуация, когда неполна информация, характеризующая другие этапы анализа. Упомянем лишь в качестве примера случай, когда мы постулируем только вид, но не параметры функции Q- и P-мер на множестве образующих G и множестве конфигураций 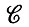(см. т. 1, гл. 2).

Резюмируя, мы будем стараться определить синтез изучаемого образа настолько полно, насколько это допускает ситуация, с тем, чтобы обеспечить максимально возможную глубину и эффективность анализа.