1.2. Свойства операторов изображений

Одним из основных объектов изучения в анализе образов является отображение одной алгебры изображений в другую, и поэтому необходимо рассмотреть операторы изображений, реализующие подобные отображения. Не требуя полной общности, мы будем обычно полагать, что выполняется следующее условие.

Условие 1.2.1. (i) Механизм деформации 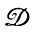регулярен (см. т. 1, Определение 4.1.1).

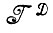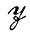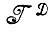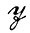(ii) Оператор изображения f отображает в некоторую алгебру изображений с теми же преобразованиями подобия S, образующими по предположению группу, причем и , и представляют собой сепарабельные метрические пространства, а оператор изображения f измерим по Борелю.

Функция расстояния будет обозначаться символом 6 с добавлением нижнего индекса, когда необходимо указать, какая именно функция используется, если их несколько.

Это условие выполняется в большинстве из встречающихся в последующих главах случаев. Естественно, может встретиться случай, когда отображение в алгебру 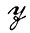производится не из алгебры деформированных изображений 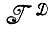, а из какой-либо другой, скажем алгебры идеальных изображений 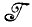, и тогда приходится прибегать к вполне очевидным модификациям. Если оператор изображения f определяется на 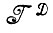, то выделяются следующие три случая:

(а) Искомая алгебра изображений 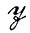⊃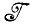, так что значения оператора изображения менее структурированы, чем идеальные изображения. Аппроксимация образа (см. разд. 1.1) обладает более простой структурой, чем алгебра идеальных изображений .

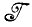(б) Противоположным случаем является 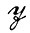⊂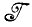. Примером служит ситуация, когда мы хотим построить разбиение алгебры идеальных изображений и выбрать по одному представителю из подмножеств, принадлежащих разбиению. Эти представители (принадлежащие алгебре идеальных изображений 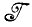) и составят элементы искомой алгебры изображений 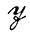. Такая процедура ведет к увеличению структуризации: описание образа обладает более сложной структурой, чем алгебра идеальных изображений .

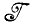(в) Промежуточный случай возникает при и он будет 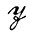= 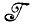изучаться наиболее подробно. Этот случай представляет собой восстановление образа и соответствует сохранению структуры.

Мы не требуем, чтобы оператор изображения f обязательно был непрерывным. Если он не непрерывен, то множество точек разрыва оператора изображения f представляет существенный интерес.

Точно так же мы не требуем, чтобы оператор изображения имел обращение. Введя множество

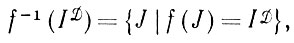(1.2.1)

по его размеру, например диаметру, можно получить некоторое представление о том, насколько "вырожденным" является f.

Точно так же, как для деформаций, понятия гомоморфизма, ковариантности и ковариантности по вероятности (см. т. 1, разд. 4.1) можно ввести для оператора изображения f. Последнее, в частности, означает, что для всякого преобразования подобия s распределения вероятностей f()sI^D и sf(I^D) одинаковы; этот факт мы записываем так:

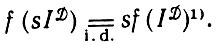(1.2.2)

^* ( i.d. - identically distributed (англ.)-одинаково распределенные. - Прим. перев.)

Отметим, что если деформации также ковариантны по вероятности, то

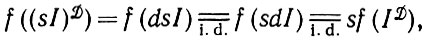(1.2.3)

т. e. оператор изображения, примененный к деформированным вариантам sI, ведет себя в вероятностном отношении точно так же, как если бы он применялся к деформированным вариантам идеального изображения I, а результат его применения был подвергнут преобразованию подобия s. Это привлекательное свойство инвариантности будет довольно часто встречаться при рассмотрении конкретных случаев.

Преобразования подобия и деформации определяются заданием структуры образа, а их отношения, выраженные через ковариантные свойства, следуют из введенных допущений. Иначе обстоит дело с оператором изображения f: структура образа не задает его непосредственно. Вместо этого приходится рассматривать все семейство F, причем выбор F особенно сильно зависит от вычислительных ограничений. В пределах семейства F мы ищем "хороший" в смысле некоторого критерия вариант f, но априори нет никаких оснований считать, что он будет обладать какими-либо определенными свойствами, существенными для теории образов. Эта проблема будет обсуждаться в разд. 1.3 и 1.4.

Допустим, что мы рассматриваем восстановление изображения f: 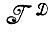→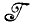. Деформированные варианты I^D = dl заданного идеального изображения имеют на 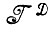вероятностную меру P_I. Если имеются два идеальных изображения I₁ и I₂, то существуют две вероятностные меры P_I1 и P_I1. Если эти меры близки, то, очевидно, трудно определить, какое из идеальных изображений, I₁ или I₂, породило наблюдаемое деформированное изображение I^D, и, наоборот, если вероятностные меры P_I1 и P_I2 сильно отличаются друг от друга, то разделение не вызывает затруднений. Точнее это можно выразить так:

Пусть Е - борелевское множество, принадлежащее 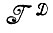. Предельный случай возникает, если можно отыскать Е, такое, что

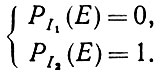(1.2.4)

В таком случае оператор изображения f можно определить как

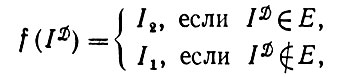(1.2.5)

и тем самым достигается совершенно точное разделение идеальных изображений I₁ и I₂:

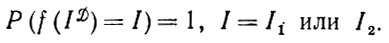(1.2.6)

Однако все это слишком хорошо для того, чтобы встречаться в реальных условиях. Противоположный условию (1.2.4) крайний случай заключается в том, что для всякого борелевского множества Е с мерой P_I1(Е) = 0 мера Р_I2(Е) = 0 и наоборот. На языке теории меры это означает, что эти две меры эквивалентны и абсолютно непрерывны относительно друг друга (см. например, монографию Халмоша (1950)). В таком случае известно, что вероятностную меру можно записать в виде интеграла

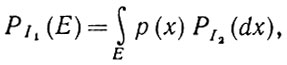(1.2.7)

где неотрицательная функция р - производная Радона - Никодима от меры P_I1 по мере Р_I2, имеющая вид

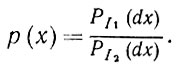(1.2.8)

Чтобы упростить запись, здесь для обозначения изображения I использована переменная x. Действительно, в случае эквивалентности производная Радона - Никодима р строго положительна почти наверное и вероятностную меру P_I2 можно записать в виде интеграла от вероятностной меры Р_I1 аналогично уравнению (1.2.7) с той разницей, что роль р будет выполнять выражение 1/р.

Одной из первоочередных задач при восстановлении изображения является проверка, эквивалентны ли P_I-меры, что часто имеет место, и последующее вычисление производной Радона - Никодима, что не всегда просто. Следующие замечания окажутся полезными во многих случаях.

В общей теории образов на математические свойства деформированных изображений в отличие от идеальных не налагается существенных ограничений. Будет, однако, справедливо заметить, что алгебру деформированных изображений 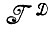часто можно рассматривать как некоторое топологическое векторное пространство или как вложение в него. Нам, следовательно, придется работать с вероятностными мерами, заданными на подобных пространствах, т. е., другими словами, со случайными процессами.

В связи с этим в анализе образов можно использовать методы, развитые применительно к статистическому выводу в теории случайных процессов; работа в этом направлении была начата в монографии автора (1950) (см. также отчет автора 1967 г.), и к настоящему времени здесь уже сделано довольно много. Мы приведем основные результаты этой теории, которые будут применяться в различных модификациях.

Допустим, во-первых, что деформированное изображение x параметризовано в виде вектора x = (x₁, x₂, x₃, ...), где координаты x_i будем называть наблюдаемыми координатами. Подобную параметризацию обычно можно осуществить различными способами, и выбор связан с вопросом о том, каким образом удобнее обеспечить получение наблюдаемых координат с простыми вероятностными свойствами. Допустим также, что для всякого натурального числа nР_I1 - распределение y_n = (x₁,x₂ ..., x_n) - абсолютно непрерывно относительно Р_I2 на той же σ-алгебре n-мерных цилиндрических множеств. Воспользуемся классическим разложением меры Р_I1 на абсолютно непрерывную и сингулярную относительно меры Р_I2 составляющие:

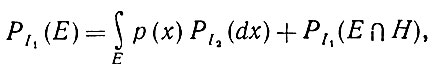(1.2.9)

где р_n(x) - производная Радона - Никодима. Н в уравнении (1.2.9) -это фиксированное борелевское множество P_I1-меры нуль, но не P_I2-меры нуль, за исключением того случая, когда P_I2 абсолютно непрерывна относительно P_I2.

Следующий результат понадобится нам несколько раз в дальнейшем.

Теорема 1.2.1.При сформулированных условиях имеет место следующее:

(1.2.10)

При соответствующем выборе подпоследовательности {р_n(х)} данное утверждение будет справедливо со сходимостью почти наверное вместо сходимости по вероятности.

Важность этого результата связана с тем обстоятельством, что n-мерные плотности распределений р_n часто можно вычислить в замкнутой форме. Используя (1.2.10), можно проверить выполнение условия Р_I2(Н) = 0, что представляет наибольший интерес с практической точки зрения, и найти производную Радона - Никодима р.

Доказательство теоремы 1.2.1 можно найти в работе автора (1950), а его упрощенный вариант в отчете автора (1967).

Кроме того, если ввести параметризацию с помощью наблюдаемых координат (xⁿ₁, xⁿ₂,...,xⁿ_n) Для всех натуральных чисел n, то соотношения (1.2.10) будут также справедливы, но с очевидными изменениями. Этим приемом можно воспользоваться, как мы убедимся в гл. 5, когда, например, деформации превращают идеальное изображение в точечное изображение.

Итак, анализ образов естественно связать с теорией вывода в случайных процессах. Это корректная процедура, однако не следует недооценивать аналитических трудностей. В общей теории образов рассматривается множество различных видов изображений, в теории же случайных процессов основным является случай, когда аргумент -действительный, а значение действительное или комплексное. Пространством реализаций могут в таком случае быть пространства L₂(a, b), С (а, b) или какое-нибудь другое известное функциональное пространство. В отличие от этой ситуации мы часто будем сталкиваться с алгебрами изображений, свойства которых не столь широко известны и при этом нельзя будет просто сослаться на результаты, полученные в теории вывода для случайных процессов.

После вычисления р можно приступать к задаче отыскания подходящих операторов изображения. В первую очередь, однако, следует определить, чего мы хотим добиться с помощью анализа образов, посредством явного критерия, оценивающего его качества.