6.3. Исходная сеть

Входные векторы, принадлежащие алгебре изображений, будут обрабатываться с помощью основного процессора образов Ω - сети, состоящей из ячеек, аналогичных рассматривавшимся в разд. 3.5. Реальные нервные сети обнаруживают значительную регулярность. Топология подобных сетей, задающая способ соединения ячеек сети между собой, очевидно, определена генетически, по крайней мере на глобальном уровне, и поэтому соединения, несомненно, не являются абсолютно случайными. С другой стороны, топологические характеристики могут быть разными у отдельных особей, относящихся к одному и тому же виду высших животных. Модель подобной сети будет, таким образом, включать управляемые вероятности соединений, причем значения вероятностей не одинаковы, а определяются расстоянием и, возможно, другими характеристиками.

В связи с этим мы будем рассматривать сеть только в том виде, какой она имеет в момент рождения: все изменения, происходящие позже в течение жизни Ω из-за влияния среды, откладываются до разд. 6.5.

Мы будем изучать спектральные свойства сетей, основанных на указанной модели и рассматриваемых как линейные операторы. Когда в такую сеть подается сигнал, то соответствующую реакцию можно представить через спектральные свойства оператора, и мы убедимся в том, что спектральная мера с увеличением размера сходится к общему пределу при соблюдении слабых условий, которые ниже будут уточнены.

Практическим следствием этого является выполнение для подобных сетей закона больших чисел для спектров, и потому по достижении больших значений размера влияние случайных факторов на топологию будет уменьшаться. Прежде чем приступить к доказательству этого результата, сделаем несколько предварительных замечаний. Наше исходное допущение заключалось в том, что предельный спектр имеет меру, сосредоточенную в одной точке,- одиночный пик. К нашему удивлению, машинные эксперименты показали, что на самом деле имеет место иная ситуация, и мы пришли к совершенно другому предположению, сформулировав его в виде теоремы.

Рассмотрим некоторую сеть, состоящую из двух множеств узлов: входов с нумерацией i = 1, 2, ..., n и выходов с нумерацией j = 1,2, ..., m. Эти узлы являются ячейками сети - нейронами. Между некоторыми из i-узлов и j-узлов установлены синаптические связи. Связи между i-узлами, так же как и связи между j-узлами, отсутствуют.

Очевидно, что реальные нервные сети совершенно неоднородны и обладают характерной трехмерной архитектурой. Для упрощения анализа, который все равно будет нелегким, мы пожертвуем неоднородностью и трехмерностью.

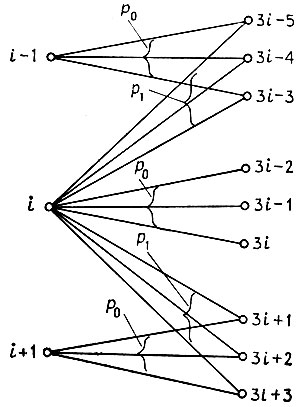
Рис. 6.3.1

Значения n и m очень велики, и m = dn, причем предполагается, что коэффициент расхождения d - целое число. Нас особенно интересуют расходящиеся сети, d > 1.

Множество вероятностей {pⁿ_h; h = - s, - s+ 1, ..., s} управляет установлением соединений. Для некоторого заданного значения i соединение i → j = (i + h)×d - e (e = 0, 1, 2,..., d - 1) будет существовать с вероятностью

(6.3.1)

Число s < n/2 называется размахом сети. На рис. 6.3.1 приведен пример соединений при d = 3, где часть соединений исключена. На рис. 6.3.2 приведена матрица вероятностей соединений для случая n = 5, d = 2, s= 1. Отметим циклическое расположение вероятностей, введенное исключительно ради математического удобства с тем, чтобы избежать ненужных усложнений.

Тогда средняя связность С_n определяется как

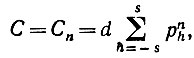(6.3.2)

и мы будем считать, что С_n → ∞ с увеличением n. Если i соединено с j, то будем считать, что прочность υ_ij - этого соединения равна +1 или -1 с вероятностью 1/2 для каждого значения. Все ситуации выбора разрешаются независимо друг от друга.

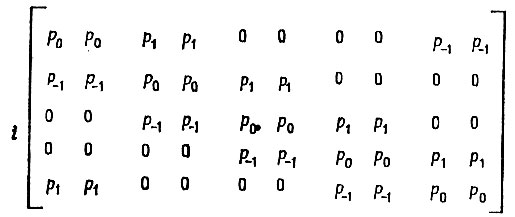
Рис. 6.3.2.

В результате получаем прямоугольную матрицу V = (υ_ik), которую можно рассматривать как линейный оператор, подающий в процессор некоторый входной вектор x = {x_i}, причем л; выполняет роль y(c). Нас, в частности, интересует, проявляет ли этот оператор к определенным векторам x большую благосклонность, чем к другим: как нормированная энергия (1/C)||V^Tx||² = x^TWx, W = (1/С)VV^T изменяется с изменением x при ||x|| = const? Каковы спектральные свойства оператора W?

Исходная сеть была построена по случайной (хотя и не чисто случайной) конструкции, соответствующей гипотезе о том, что генетически определена лишь статистическая топология (см. т. 1, разд. 3.5), но не ее детали. Однако если это так, то как можно объяснить одинаковые способности у различных особей одного и того же вида? Мы попытаемся ответить на этот вопрос, изучая общие свойства реализаций нашей модели. Опираясь на высокую размерность сети, мы пытаемся сформулировать и доказать предельные теоремы, которые могут быть к ней применены и из которых следует, что особи одного вида обладают (асимптотически) оператором с одинаковыми спектральными свойствами.

Мы считали, что первоначально предельная спектральная мера, соответствующим образом нормированная, будет иметь носитель, состоящий всего из одной точки, λ = 1. Для накопления данных было проведено несколько численных экспериментов при n = 40, s = 2 и

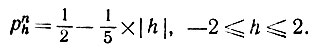(6.3.3)

На рис. 6.3.3 приведены соответствующие распределения собственных значений для нескольких типичных случаев. Совершенно очевидно, что собственные значения не группируются вокруг λ = 1, особенно при малых значениях коэффициента расхождения d.

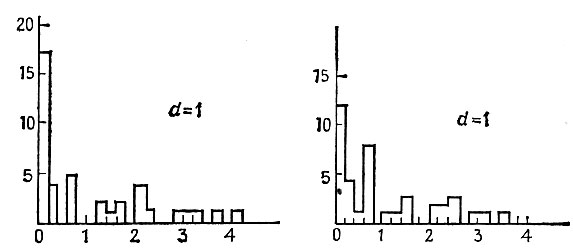
Рис. 6.3.3

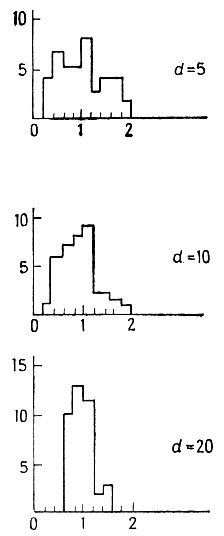
Рис. 6.3.3

Ситуация оказалась сложнее, чем мы предполагали, и поэтому следует провести более глубокий анализ задачи. Для начала отметим, что нашим объектом изучения сейчас являются спектральные свойства нормированного оператора W при больших значениях n. Это симметрический и неотрицательно определенный случайный оператор. Обозначим его собственные значения через λ⁽ⁿ⁾_i i = 1, 2, ..., n, и рассмотрим спектральную меру, заданную как спектральная функция распределения

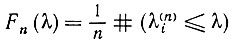(6.3.4)

на неотрицательной части действительной оси. Разумеется, F_n(λ) - это вероятностный процесс. Основная проблема здесь заключается в том, сходится ли F_n и является ли соответствующий предел общим, т. е. не зависящим от управляющих вероятностей.

Результат нашего анализа можно представить в виде отдельного предложения.

Предложение 6.3.1. Допустим, что С → ∞ при n → ∞. Пусть при заданном

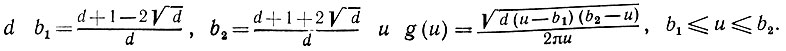
Тогда для каждого λ последовательность {F_n(λ)} сходится по вероятности к спектральной мере

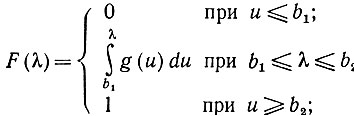(6.3.5)

которая зависит только от d.

Доказательство не из легких, но в настоящее время мы не надеемся, что его удастся упростить. Наша стратегия доказательства базируется на восьми леммах. В первую очередь выводятся предельные значения математических ожиданий моментов собственных значений, т. е.

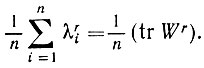
Затем с помощью комбинаторного приема мы показываем, что эти значения являются решением некоторого разностного уравнения. Далее мы докажем, что моменты сходятся по вероятности к этим значениям. После этого решим разностное уравнение с помощью производящей функции, перейдя в комплексную область, и получим в результате F(λ). Мы завершим доказательство, показав с помощью доводов из теории меры сходимость по вероятности F_n(λ) к F(λ).

Доказательство. Мы начнем со случая, когда отсутствует расхождение, т.е. когда d = 1. Наша первая задача - определить для каждого целого значения r ≥ 1 предельное значение

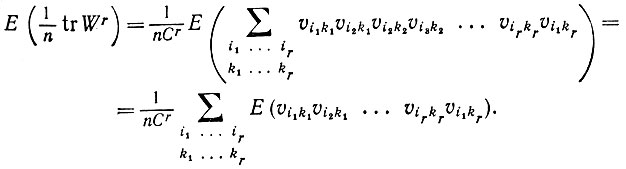(6.3.6)

Многие члены этого выражения равны нулю в (6.3.6) ненулевыми являются лишь те члены, в которых каждое входящее в соответствующий член υ_ik повторяется четное число раз. Рассмотрим один из способов подобной группировки υ_ik. Так, например, один из способов заключается в том, чтобы взять все члены, у которых (i₁, k₁) = (i₂, k₁), (i₂, k₂) = (i₃, k₂) =...= (i₁, k_r) и (i₁, k₁) ≠ (i₂, k₂). В настоящем примере имеются две группы. Другим способом группировки является объединение всех тех членов, в которых υ_ik равны. Можно просуммировать (6.3.6) по каждому типу группировки. Если выбран один из них, то при Р_ij = Рⁿ_ij получаем

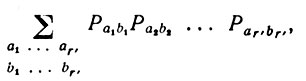(6.3.7)

где r'≤ r и связи между a₁, a₂,...., a_r', b₁, b₂,..., b_r' определяются начальными условиями. Отметим, что суммирование проводится не по всем значениям a₁, a₂,...., a_r', b₁, b₂,..., b_r' поскольку, например, (a₁, b₁) не может равняться (a₂, b₂). Рассмотрим в качестве примера случай, когда г = 3. Тогда (6.3.6) принимает вид

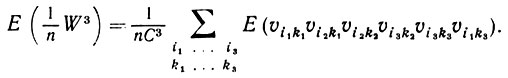(6.3.8)

Отметим, что некоторые группировки неосуществимы. Так, например, нельзя объединить с υ_i1k1 и υ_i2k2 оставлять υ_i2k1 в другой группе, поскольку (i₁, k) будет равна (i₂, k₂), в результате чего υ_i2k1 = υ_i1k1 = υ_i2k2 Один из допустимых способов группировки заключается в том, чтобы принять (i₁, k₁) = (i₂, k₁) = (i₂, k₂) = (i₃, k₂), (i₃, k₃) = (i₁, k₃) и (i₃, k₃) ≠ (i₁, k₁). Обозначив индексы первой группы через (a₁, b₁) и второй - через (a₂, b₂), переписываем выражение (6.3.7) в следующем виде:

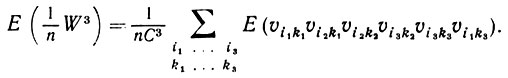(6.3.9)

Здесь r'= 2, и мы должны связать a₁ с а₂. Очевидно, что мы не берем члены, в которых (a₁, b₁) = (a₂, b₂). Отметим, что b₁ и b₂ свободны в том смысле, что они не связаны друг с другом.

Пусть при заданном r S_r есть множество всех группировок, таких, что всякая s∈S_r будет вносить непренебрежимо малый вклад в Е((1/n) tr W^r) в пределе.

Лемма 6.3.1.Для каждой группировки s∈S^r, r' = r, т.е. s∈S^r обеспечивает точный подбор пар υ_ik.

Доказательство. Можно ограничить (3.6.3), удалив в первую очередь все пары a_jb_j, в которых либо a_j, либо b_j не связаны (отметим, что для каждого Р_ab либо a, либо b должны повторяться в другом множителе). Каждый раз, когда удаляются одиночные элементы, можно ограничить величину (6.3.7), исключая Р_ajbj вместе с индексами a_jb_j - и умножая полученную в результате сумму на С. После того как это сделано, выбираем любой b_j и проводим по нему суммирование. Если имеется t множителей Р_aj'bj', таких, что b_j связан с b_j', то сумму можно ограничить, удалив эти t множителей и их индексы и умножив результат на

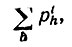
поскольку

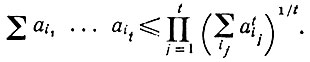
Отметим, что для каждого исключенного Р_ajbj. существует еще некоторый P_aj'bj', У которого a_j и b_j, связаны друг с другом и который не исключен, поскольку все свободные индексы были уже исключены прежде. Далее удаляются все одиночные O_ajbj затем множители и т. д. В результате мы получаем верхнюю оценку для выражения (6.3.7):

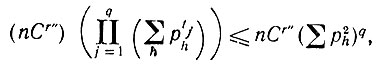(6.3.10)

где

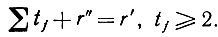
Если на каждом шаге удаляются только одиночные P_ajbj, то второго множителя явно не будет. В этом случае положим q = 0. Поскольку очевидно, что

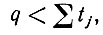
мы видим, что из r' < r следует

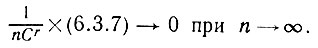
Отметим, что каждый раз, когда при доказательстве мы прибегали к группировке, ее можно было бы осуществлять по a_j - вместо b_j. Очевидно также, что для s∈S_r q = 0. Итак, можно заключить, что S_r - это множество всех связей, обеспечивающих точное спаривание υ_ik, и на каждом шаге (как это было сделано в лемме 6.3.1) одиночный Р_ajbj. может быть исключен.

Лемма 6.3.2. Для каждой s∈S_r величина (6.3.7) ~nС^r, и, следовательно, Е((1/n) tr W^r) → f (r) ≡ числу элементов в S_r при n → ∞.

Доказательство. При заданной s∈S_r либо какой-то a_j, либо какой-то b_j свободны. Пусть свободен b_j (a_j, конечно, не свободен). Тогда

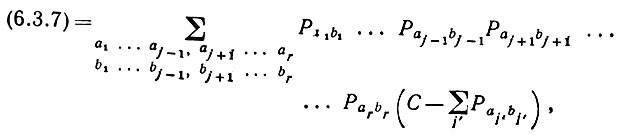(6.3.11)

где диапазон значений j' включает индексы, для которых (a_j, b_j) = (a_j', b_j'). Поскольку, однако, из (6.3.10) следует, что

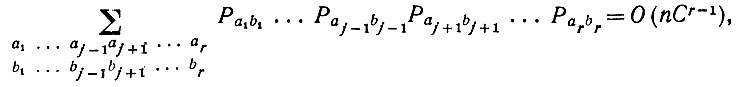
и поскольку

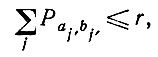
то мы получаем, что

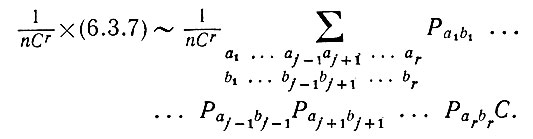(6.3.12)

Очевидно, что такую операцию можно осуществить на каждом шаге. Следовательно, (6.3.7) ~nС^r.

Мы вводим инструмент, который позволит нам получить рекуррентное соотношение для {f(r)}^∞_r=1. Будем называть его циферблатной нотацией. Основные обозначения приведены на рис. 6.3.4.

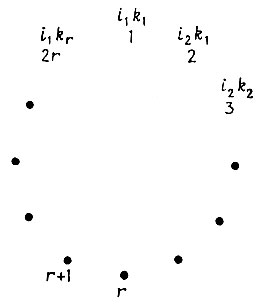
Рис. 6.3.4

Каждый номер соответствует некоторому а индексы представляют исходные связи. С помощью циферблатной нотации можно полностью охарактеризовать некоторую s∈S_r. Для каждой пары υ_ik проведем прямую, соединяющую номера, соответствующие элементам этой пары. Каждый номер в таком случае будет иметь одну и только одну исходящую из него прямую. Каждая прямая будет соответствовать некоторому Р_ajbj и наоборот. Нетрудно убедиться в том, что одиночный Р_ajbj может быть исключен только тогда, когда соответствующая ему прямая соединяет два соседних номера циферблата. Всякий раз, когда исключается некоторая пара, две позиции на циферблате, ближайшие к этой паре, можно считать соседними, и, следовательно, возникает циферблат соответствующий некоторой s∈S_r-1. Если, например, в пару объединены 1 и 2, то их можно удалить и соседними становятся позиции 2r и 3, поскольку i₁ и i₂ должны быть связаны. Можно продолжать эту процедуру до тех пор, пока все пары не будут исключены.

Линии группировки s∈S_r не могут, однако, пересекаться (при циферблатном представлении), поскольку пару исключать можно только тогда, когда все номера, расположенные между ее элементами (на обеих частях циферблата), исключены. Это невозможно, если две линии пересекаются. Следовательно, можно сформулировать такую лемму.

Лемма 6.3.3. S_r⊆B_r, где В_r - множество всех соединений (при заданном r), причем циферблатное представление характеризуется точным объединением в пары и отсутствием пересечений.

Нетрудно убедиться, что при любом b∈B_r, таком что Р_ajbj может быть исключен, полученная в результате связь будет принадлежать множеству В_r-1.

Лемма 6.3.4. S_r = B_r.

Доказательство. Нам остается показать, что при любом r' ≤ r из b∈В_r', следует, что Р_ajbj. можно исключить. Тогда b∈В_r должно принадлежать S_r.

Утверждение. При r ≥ 2 b∈B_r имеет по крайней мере два Р_ajbj, которые можно исключить. Мы докажем это, используя индукцию по r и циферблатную нотацию. Случай r = 2 очевиден. Допустим, что это справедливо для всех r' ≤ r. Представим заданное b∈B_r+1 в циферблатной нотации. Пусть 1 объединена в пару с m.

Случай 1. Прямая разделит циферблат на две части: одна из них представляет b∈B_r1, другая представляет аналогичный элемент множества В_r2, r₁, r₂ ≤ r. Если и r₁ и r₂ ≥ 2, то из гипотезы индукции следует, что в каждой части циферблата имеются по крайней мере две смежные пары, причем по крайней мере одна пара, расположенная на каждой из сторон, должна присутствовать на исходном циферблате. Если r₁ или r₂ или они оба равны 1, то очевидно, что на исходном циферблате будут две пары.

Случай 2. m = r или 2. Тогда одной парой является <<1 - m >> а на остальной части циферблата, представляющей некоторую связь в В_r, расположены две пары, причем по крайней мере одна из них имеется на исходном циферблате.

Лемма 6.3.5. При f(0) ≡ 1 мы имеем

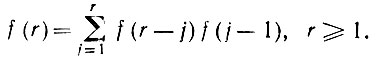(6.3.13)

Доказательство. Подсчитаем просто число возможных конфигураций на циферблате. 1 можно соединить с 2, 4, 6,....,2r. Для пары <<1 - 2>> получаем f(0)f(r - 1). Для пары <<1 - 4>> получаем f(1)f(r - 2) и т.д. Следовательно, (6.3.13) справедливо.

Рассмотрим далее

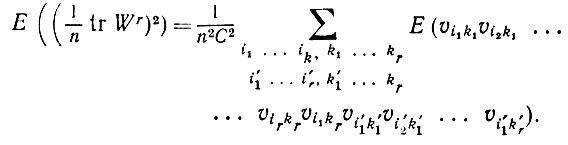(6.3.14)

Мы снова убеждаемся, что только те члены не обращаются в нуль, υ_ik которых объединяются в пары. Для некоторого заданного типа образования пар можно записать

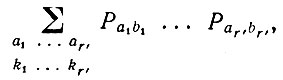(6.3.15)

причем связи, наложенные на a₁, ..., a_r, b₁, ..., b_r определяются исходными ограничениями. Как и в лемме 6.3.1, нетрудно убедиться в том, что этот способ построения пар может внести непренебрежимый вклад в величину Е (((1/n) tr W^r)²) в пределе только, если r' = 2r. Кроме того, ни на одном шаге нельзя удалить Р_ajbj, представляющий собой объединение υ_ik и υ_i'k' поскольку ни a_j, ни b_j не будут свободны. Мы можем исключить лишь такой Р_ajbj, который объединяет в пары соседние υ_ik или соседние υ_i'k'. На основании индукции мы приходим к выводу, что

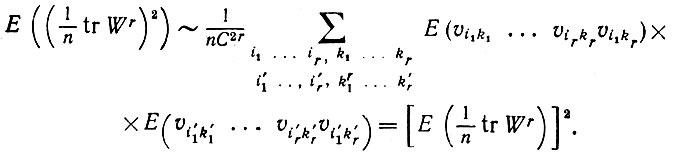(6.3.16)

Следовательно, Var ((1/n) tr W^r) → 0.

Лемма 6.3.6.Величина (1/n)tr W^r сходится по вероятности к f(r).

Доказательство. При заданном ε > 0 получаем, что

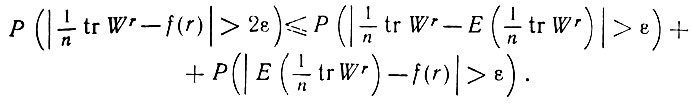(6.3.17)

На основании неравенства Чебышева получаем следующее:

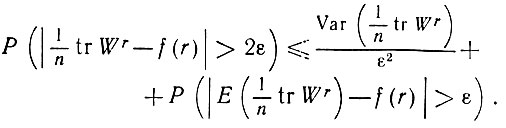(6.3.18)

Поскольку оба члена стремятся к нулю при n → ∞, доказательство закончено.

Обобщим теперь полученные результаты на случай, когда соединения расходятся с коэффициентом расхождения 1. Матрица V = (υ_ij) будет иметь размер n × dn.

Как и прежде, соединения будут циклическими. Напомним, что теперь

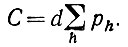
Для заданной строки, суммируя вероятности в столбцах, получаем С. Для заданного столбца сумма вероятностей по строкам дает C/d (см. рис. 6.3.2). Будем действовать тем же способом, что и в случае d = 1. Связи, налагаемые на индексы при оценивании Е ((1/n) tr W^r), те же самые, за исключением того, что показатель каждой связи не будет равен 1. При каждом исключении некоторого Р_ajbj. мы получаем С, если исключение основано на суммировании по b_j, и C/d, если суммирование проводится по a_j, за исключением случая, когда мы доходим до конца, поскольку

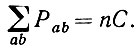
Пусть

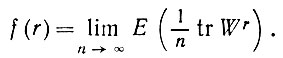
Случай произвольного d трактуется так же. Подробности доказательства можно найти в отчете Гренандера и Силверстайна (1974); здесь мы приведем только результат: при f(0) ≡ 1 справедлива следующая лемма.

Лемма 6.3.7.

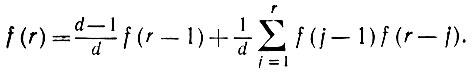(6.3.19)

Замечание. И при d = 1, и при d > 1 имеет место квадратное разностное уравнение. Ключевым является то обстоятельство, что это уравнение типа свертки, и, следовательно, для его решения можно воспользоваться методом производящих функций.

Лемма 6.2.8.Производящая функция G, задаваемая как

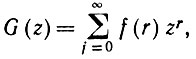
является полностью определенной и аналитической в окрестности 0 на комплексной плоскости.

Доказательство. Вспомогательная функция

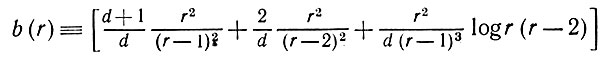
ограничена сверху для всех r ≥ 3, так что можно найти a ≥ 1, при котором f(2) ≤ a²/4 и b(r) ≤ a. Покажем по индукции, что f(r) ≤ a^r/r² при r ≥ 1. Поскольку f(1) = 1, случаи r = 1, 2 уже доказаны. Допустим, что наше утверждение справедливо для всех r' < r, r ≥ 3. Тогда

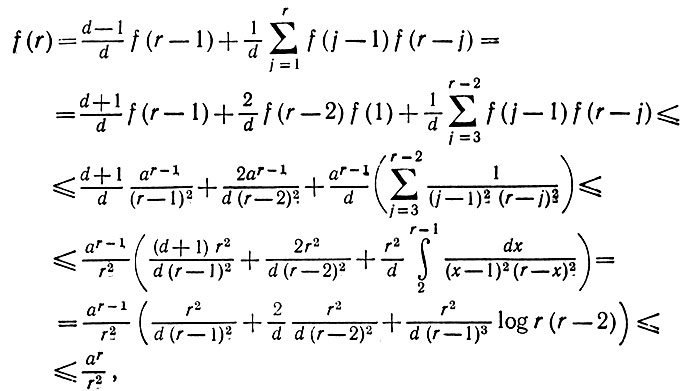(6.3.20)

и, следовательно, лемма 6.3.8 справедлива.

Нетрудно найти G(x), x∈R, в окрестности начала координат. Пусть - функция свертки

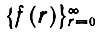
с ней же, a G - производящая функция

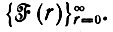
Тогда

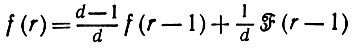(6.3.21)

и

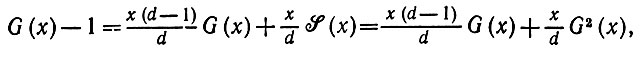(6.3.22)

так что

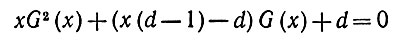(6.3.23)

И

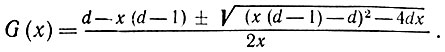(6.3.24)

Поскольку G (0) = 1, то мы приходим к выводу, что для z в некоторой окрестности начала координат на комплексной плоскости имеет место следующее:

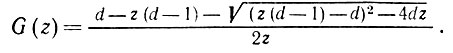(6.3.25)

Отметим, что в связи с наличием в (6.3.24) квадратного корня необходимо соблюдать осторожность при аналитическом продолжении G, т. е. следует продолжать G на правую ветвь римановой поверхности.

Определим функцию

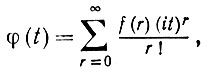(6.3.26)

воспользовавшись следующей теоремой (Титчмарш (1939)). Если

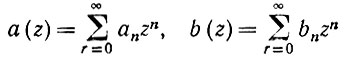
обе аналитические в некоторой окрестности 0, то

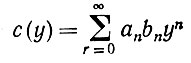
аналитическая в окрестности 0 и может быть задана с помощью

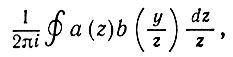(6.3.27)

где контур окружает начало координат, и в нем a(z) и b(y/z) аналитические. При a(z) = G(z), b(z) = e^z имеем

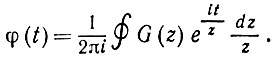(6.3.28)

При d ≥ 2

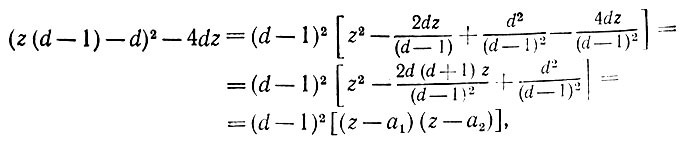(6.3.29)

где a₁ и a₂ (при a₁ < a₂) определяются

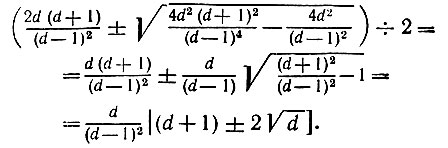(6.3.30)

Нетрудно убедиться в том, что

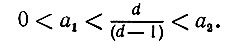
Следовательно, при d ≥ 2

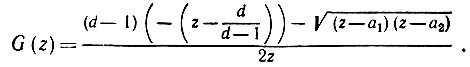(6.3.31)

При d = 1 мы получаем

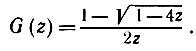(6.3.32)

В первую очередь рассмотрим случай d ≥ 2. G(z) можно записать как

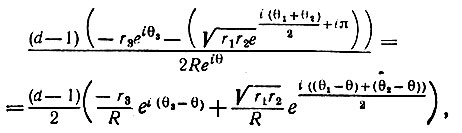(6.3.33)

где R, r₁, r₂, r₃, θ, θ₁, θ₂, θ₃ представлены на рис. 6.3.5. Причина присутствия n в показательной функции состоит в том, что квадратный корень должен быть положителен на оси действительных чисел слева от a₁ т. е. при θ = θ₁ = ₂ = θ₃ = π. Из элементарной тригонометрии известно, что при R → ∞ (r₁)/R → 1 и θ_i → 0, i = 1,2,3. Из (6.3.32) следует, что при R ↓ G (z) → 0 при всех θ.

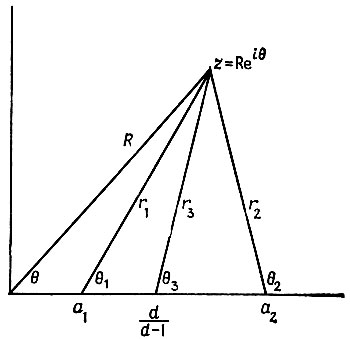
Рис. 6.3.5

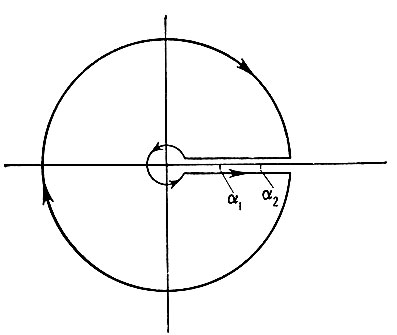
Рис. 6.3.6

Мы интегрируем вдоль пути, показанного на рис. 6.3.6. Учитывая, что функция квадратного корня имеет разрыв на прямой между a₁ и a₂, в пределе получаем

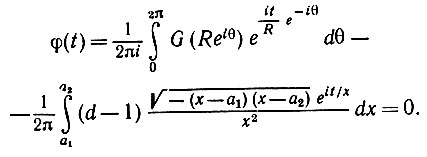(6.3.34)

Поскольку

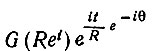
равномерно ограничена для всех R, то на основании теоремы Лебега о сходимости заключаем, что второй член в (6.3.34) сходится к нулю.

Следовательно,

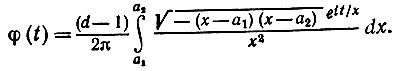(6.3.35)

Положив u = (1/x), получаем, что

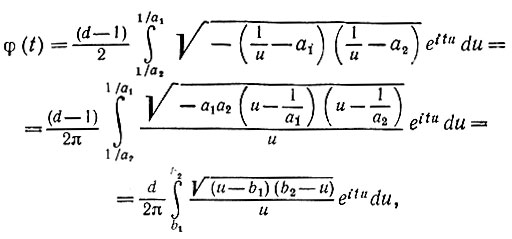(6.3.36)

где

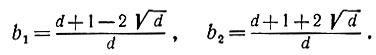
При d = 1 действуем так же, учитывая, что функция квадратного корня должна быть равна - 2i√r₁e^iθ₁/2 (см. рис. 6.3.7).

Поскольку G (Re^iθ) → 0 равномерно по 0 при R → ∞, то приходим к следующему:

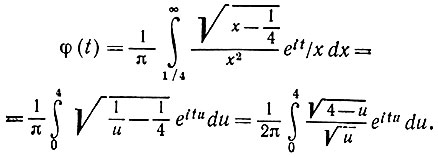(6.3.37)

Объединяя эти два результата, получаем

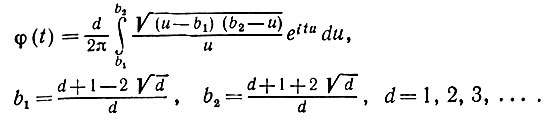(6.3.38)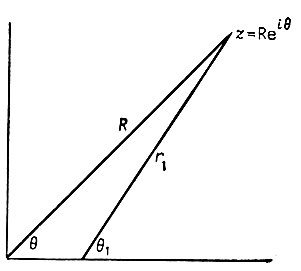

Рис. 6.3.7

Элементарный интеграл

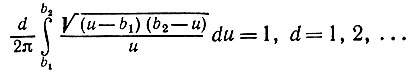(6.3.39)

вычислить нетрудно. Поскольку очевидно, что φ(t) может быть аналитически продолжена на всю R, то φ(t) является характеристической функцией распределения вероятностей G с плотностью

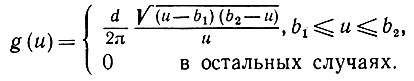(6.3.40)

Поскольку φ(t) - аналитическая функция в окрестности 0, то G - единственное распределение, обладающее моментами

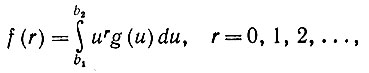(6.3.41)

и, следовательно, F, определенная в предложении, однозначно задана своими моментами.

Теперь мы можем закончить доказательство теоремы. Пусть

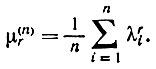
Нам известно, что

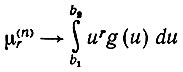(6.3.42)

по вероятности при n → ∞. Задав произвольную подпоследовательность 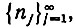, можно найти некоторую подпоследовательность

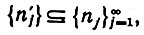
так что

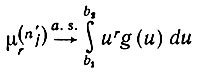(6.3.43)

для всех r. Поскольку F непрерывна, то при всех λ

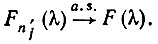(6.3.44)

Так как это может быть сделано для любой подпоследовательности натуральных чисел, то мы приходим к выводу, что

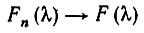(6.3.45)

по вероятности.

На этом доказательство предложения заканчивается.

На рис. 6.3.8 представлены графики g(u) при d = 1, 5, 10, 20. Их следует сопоставить с графиками, приведенными на рис. 6.3.3.

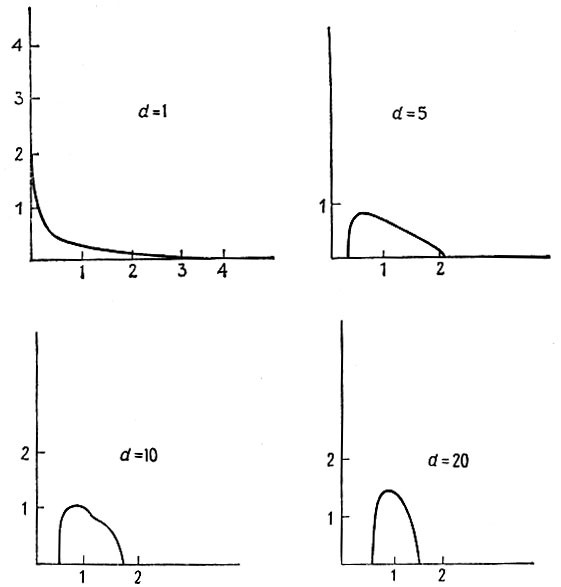
Рис. 6.3.8

Основной результат доказанной теоремы заключается в том, что случайно порожденная сеть будет иметь (почти) спектральную меру, определяемую (6.3.5). Для сетей с высокими коэффициентами расхождения эта мера сильно сконцентрирована, и можно, следовательно, допустить, что сеть в момент рождения представляет собой приблизительно постоянную, умноженную на единичный оператор.

Следует, однако, отметить, что мы не рассматривали трехмерную архитектуру сети , которой обладают реальные нейронные системы. Следовательно, вывод имеет лишь предварительный характер.