6.4. Действующая сеть

Сеть построена из нейронов, рассмотренных в разд. 3.5, соединенных между собой в соответствии со статистической топологией. Перенумеруем клетки с помощью индекса k, k = 1, 2, .. ., m.

Аксиома № 1. Функционирование сети будет описано вектором состояния ω(t) = [ω₁(t), ω₂(t), . ..,ω_m(t)], где ω_k(t) - мгновенная частота разрядов k-го нейрона. При соединении k → l часть n_kl импульсов, выдаваемых k-м нейроном, поступает в l-й нейрон. Импульсы проходят по нервным волокнам с постоянной скоростью.

Здесь m - это число нервных клеток, а не коэффициент уплотнения, как в разд. 6.2, обозначавшийся этим же символом.

Обозначим через d(k, l) длину волокна между k-м и l-м нейронами; если соединяющее их волокно отсутствует, будем считать эту длину равной +∞. Обозначим скорость распространения по волокну (предполагаемую постоянной) через υ_net.

Входной сигнал k-и клетки в момент t составляется из сигналов, порождаемых источниками, находящимися на различных расстояниях от этой клетки, и соответственно в связи с конечностью скорости распространения сигналов возникает запаздывание по времени. Суммируя, получаем входной сигнал

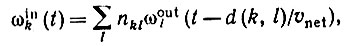(6.4.1)

к которому следует прибавить член y_k(t), представляющий добавочный входной сигнал, если k∈_in - множество клеток, на которые воздействует внешнее раздражение, а также член η_k, характеризующий вынуждающий сигнал, порождаемый собственно сетью. В данном случае мы будем считать, что η_k не зависит ни от y, ни от ω и не изменяется во времени.

С другой стороны, для сигнала на выходе того же нейрона имеем

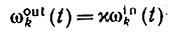(6.4.2)

(см. разд. 6.2). В результате мы приходим к системе уравнений - уравнениям сети

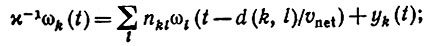(6.4.3)

здесь мы нормировали ω_k(t), вычтя из него сигнал, характеризующий спонтанную активность:

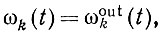(6.4.4)

где ω^out_k(t) - установившийся режим в состоянии покоя. Это объясняет причину отсутствия вынуждающего члена η_k в (6.4.3).

Знак n_kl должен быть положительным для возбуждающих входных точек (соединений) и отрицательным -для тормозящих. Поскольку мы работаем с правильными дробями, то должно выполняться условие

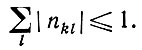(6.4.5)

Такая ситуация существует при рождении существа Ω; что происходит дальше - это совсем другой разговор.

Чтобы избежать недоразумений при рассмотрении сенсорного входного вектора y сети , отметим, что следовало бы считать dim(y) << dim(). Тем не менее мы будем предполагать равенство двух этих размерностей. Его всегда можно обеспечить формальными средствами, добавляя просто к вектору у нули для компонент, по которым отсутствует соответствие с - это обстоятельство следует иметь в виду при вычислении оператора опыта.

Сеть содержит астрономическое число клеток т, и поэтому сумму (6.3.4) можно аппроксимировать интегралом. Введем матричнозначную функцию N(L) так, что (k, l) - элемент N(L) ΔL - приближенно задается так:

(6.4.6)

Тогда наша аппроксимация оказывается матрично-векторным интегральным уравнением Вольтерра

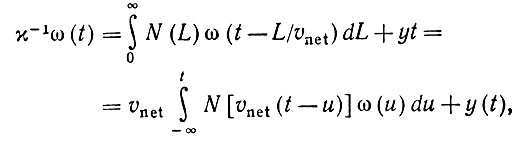(6.4.7)

где матрица полной сети определяется как

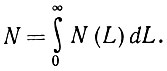(6.4.8)

Длины дендритов, естественно, ограничены. На самом деле имеется определенная эмпирическая информация для некоторых типов нейронных систем, свидетельствующая об экспоненциальном распределении длины дендритов, но в дальнейшем мы не будем этим пользоваться.

Интеграл (6.4.7) представляет пространственное суммирование в сети. Прежде чем заняться изучением (6.4.7), сделаем одно замечание относительно выбора модели. Поскольку число m огромно, вектор состояния (о принимает значения в пространстве высокой размерности и N(L) - матрицы большого размера. Эту высокую размерность следует иметь в виду. Было бы неудивительно, если бы переход к гильбертову пространству позволил лучше формализовать нашу задачу. Как бы то ни было, будем исходить из того, что число m конечное, но большое.

Наша следующая аксиома связана с коэффициентами сети.

Аксиома № 2. Коэффициенты сети n_kl должны быть симметричны, т. е. n_kl = n_lk.

Если точки соединения не содержат активных элементов, то

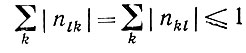(6.4.9)

или, через матрицу сети N,

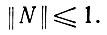(6.4.10)

Тот факт, что χ < 1, означает, что важный оператор χN ограничен по норме единицей при рождении существа Ω.

Значения n_kl при фиксированном l являются численными характеристиками свойства пространственного суммирования сети.

Определение 6.4.1.Если сеть удовлетворяет условию χ||N|| < 1, будем говорить, что сеть устойчива и имеет отображение памяти М:

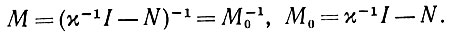(6.4.11)

Конечно, может оказаться, что даже при наличии активных элементов в соединениях сеть устойчива, но мы не можем быть в этом уверены. Подробнее этот момент будет рассмотрен в следующем разделе. Здесь же будем считать, что сеть всегда устойчива. Естественно, устойчивость имеет место и при рождении Ω.

Обратимся снова к уравнению Вольтерра (6.4.7) и будем считать, что исходное состояние сети при t = 0 - состояние покоя, ω(t) = 0, t < 0. В момент t = 0 на _in подается поле y, обладающее энергией ||y||². Напомним, что вектор y пополнен до m-мерного вектора. Хорошо известно, что решение уравнения сети (6.4.7) можно найти при помощи

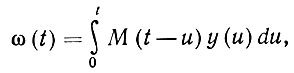(6.4.12)

где матричнозначное ядро М(⋅) можно представить рядом Неймана

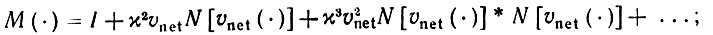(6.4.13)

звездочка здесь обозначает свертку Этот ряд сходится, если сеть устойчива.

Ряд Неймана (6.4.13) имеет привлекательную физическую интерпретацию. Допустим, что раздражитель подается в сеть только в момент времени l = 0 и только на l-ю клетку. По истечении t секунд мы наблюдаем деятельность k-й клетки - результирующая активность клетки представляет собой при этом m_kl(t), т. е. элемент (k, l) матрицы М (t). Другими словами, это фундаментальное решение уравнения системы. Фиксируя l и изменяя k и t, мы можем проследить распространение сигнала по сети .

Если бы сеть представляла собой более или менее однородную среду, как это бывает в классическом случае в акустике и оптике, то мы имели бы дело с волной, порожденной точечным источником. Хотя соответствующие волновые фронты не должны обязательно быть сферическими, они по крайней мере топологически подобны сферам.

В случае сети ситуация будет иной. Если для каких-либо ненулевых элементов N (L) распространяется на большие значения L и если метрика d(k, l) очень сильно отличается от метрики физического пространства сети, то результатом будут перескоки с одной области на другую, и поведение будет отличаться значительно меньшей регулярностью, чем явления волнового типа, используемые нами в классической физике.

Какова будет реакция сети при постоянном входном сигнале y? Уравнение (6.4.12) дает нам просто

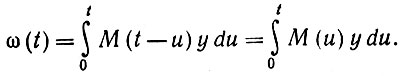(6.4.14)

При t → +∞ получаем некоторый конечный предел, достигаемый при сформулированном выше условии устойчивости:

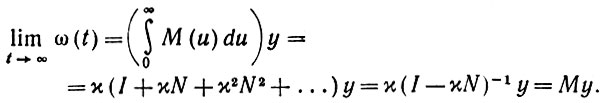(6.4.15)

Другими словами, можно сформулировать следующее предложение.

Предложение 6.4.1. Если сеть устойчива, то некоторый постоянный входной сигнал у порождает установившийся режим, определяемый отображением памяти М, примененным к y.

Отставив случай постоянства y, введем преобразования Лапласа для равномерно ограниченного y(t) при s > 0:

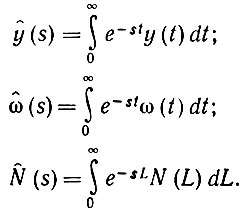(6.4.16)

Первые два из них векторнозначные, третье матричнозначное. Уравнение (6.4.7) можно представить так

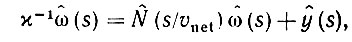(6.4.17)

и, следовательно,

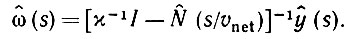(6.4.18)

В частном случае y(t) ≡ y ≡ const, разумеется,

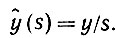
Для того, чтобы получить некоторое представление о том, насколько быстро сеть входит в установившийся режим, сформируем преобразование Лапласа от ω(t) - ω( + ∞):

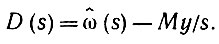(6.4.19)

Введя матрицу усредненной длины дендритов

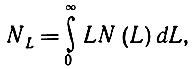(6.4.20)

можно разложить 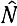в ряд Тейлора при малых положительных

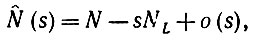(6.4.21)

и, используя (6.4.18), получаем, что

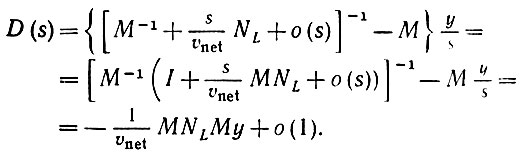(6.4.22)

Итак, D (+ o) определяется первым членом последнего выражения. Обратившись к классической теореме Таубера (см., например, Уиддер (1946)), получаем искомый результат.?

Предложение 6.4.2. В устойчивой сети установившийся режим достигается так, что

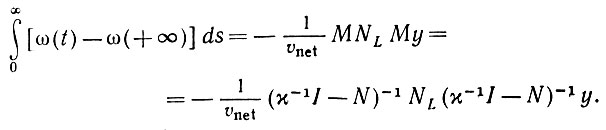(6.4.23)

Эта величина, естественно, обратно пропорциональна скорости распространения υ_net и в определенном смысле пропорциональна матрице средней длины дендритов NL. Последняя объединяется с отображением памяти М. Если у принадлежит собственному пространству N с малым по сравнению с χ^-1 собственным значением, то из (6.4.23) следует, что вектор состояния быстро устанавливается. Обратное утверждение верно не всегда, поскольку его справедливость зависит от того, как N_L связана с N.

Когда Ω быстро сканирует некоторую регулярную конфигурацию c = (g₁, g₂, ..., g_n), известно, что y приблизительно постоянен, а именно представляет собой уплотненный вариант u - линейной выпуклой комбинации всех u(g_i), i = 1, 2,..., n.

Соотношение (6.4.23) указывает, как быстро сеть придет к установившемуся режиму при данной конфигурации.

Установившийся режим, возникающий в сети при подаче постоянного сенсорного вектора y, будет, конечно, иным при N = 0. Если в момент рождения Ω сеть начинает свою деятельность с N(t) = 0, ТО ответ, определяемый обучением (модификацией) сети , на некоторую N ≠ 0 будет иметь вид

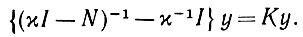(6.4.24)

Векторы y, для которых он не равен нулю, описывают сознательную сферу Ω, и мы определим подпространство сознания как

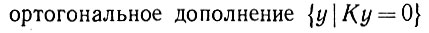(6.4.25)

и аналогично, когда мы начинаем с N(0) = εI. Если N стягивает в Y лишь пространство низкой размерности, то подпространство сознания также имеет малую размерность: Ω мало чему научилось, и наоборот.

Этой идее можно придать следующую количественную форму. При постоянном сенсорном входном сигнале для энергии установившегося режима имеем

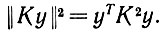(6.4.26)

Следовательно, реакция сети непосредственно связана со спектральными свойствами K и N. Общую модификацию сети можно измерить с помощью ||К|| или ||K||², и позже мы еще к этому вернемся.

Прежде чем закончить рассмотрение того, как функционирует , обратимся к представляющему определенный интерес частному случаю, когда время распространения по любому дендриту k → l постоянно, скажем h, и невелико. Эта ситуация кажется не очень правдоподобной, но заслуживает изучения, поскольку приводит к некоторым конструктивным идеям, до сих пор не исследованным.

Уравнение сети типа Вольтерра (6.4.7) можно аппроксимировать в этом случае дифференциальным уравнением

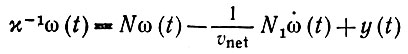(6.4.27)

(определение оператора N₁ дано в (6.4.20)). Но при этом, так как все длины L постоянны (пусть, например, они равны L₁), мы получаем, что

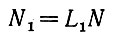(6.4.28)

и, естественно, L₁ = hυ_net. Итак, мы приходим к векторному дифференциальному уравнению первого порядка

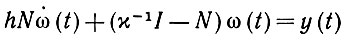(6.4.29)

или, если матрица N не особенная, к уравнению

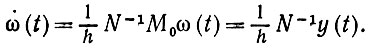(6.4.30)

При векторе начального состояния ω(0) = ω₀ уравнение (6.4.30) имеет следующее решение:

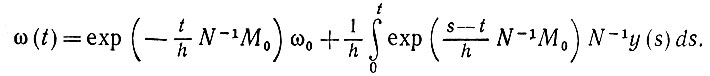(6.4.31)

Если же, с другой стороны, вариации длины дендритов существенны, то можно попытаться воспользоваться в качестве аппроксимации второго порядка двумя значениями L. Это снова приведет к некоторому дифференциальному уравнению, но на этот раз второго порядка.