6.5. Обучающаяся сеть

Функционирование сети на коротких временных интервалах можно описать уравнением (6.4.7), и мы изучили, как вектор состояния достигает определенных предельных значений при заданных условиях. Предполагается, что Ω воспринимает среду как последовательность кадров (продолжительности Δt), причем Δt. Достаточно велико для того, чтобы установившееся состояние Достигалось и поддерживалось.

В пределах подобного временного интервала Δt вектор состояния при постоянном входе y достигает установившейся величины

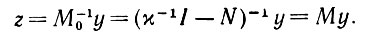(6.5.1)

В соединении (k, l) k-й и l-и клеток будем предполагать, что активность двух этих нейронов влияет на коэффициент связи n_kl (медленно) с интенсивностью, зависящей от произведения z_k и z_l и также имеющей длительный период затухания. Это означает, что модификация соединения клеток k и l не зависит от активности других клеток. В этом смысле модификация локальна.

Для ряда последовательных интервалов времени усредненный результат можно представить с помощью среднего Е (z_k, z_l),

отсюда следует естественная формализация утверждения последнего абзаца с учетом члена, представляющего затухание коэффициентов связи, т. е. забывание.

Аксиома M1. Систематическая долгосрочная модификация определяется дифференциальным уравнением

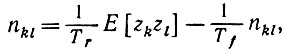(6.5.2)

где Т_r - постоянная времени запоминания и Т_f - постоянная забывания.

Данная аксиома касается лишь систематических изменений и не учитывает случайных вариаций изменений, порожденных вероятностной мерой, действующей на алгебре идеальных изображений. Случайные изменения будут рассмотрены в этом разделе позже.

Значение Т_r характеризует согласие коэффициентов связи с вектором функционирования. Значение Т_r указывает, сколь длительное предъявление необходимо для того, чтобы оказывалось воздействие на долгосрочную память. Аналогично значение Т_f показывает, через какое время модификации разрушаются. Эти величины считаются постоянными, однако, рассматривая жизнь Ω на всем ее протяжении, можно, вероятно, полагать, что к старости величина Tf возрастает: "затвердение" синапсов.

Следует отметить, что уравнение (6.5.2) справедливо только тогда, когда сеть 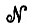устойчива; в противном случае следует использовать уравнение (6.4.7), а не только условие его устойчивости.

Важный случай, когда уравнение (6.5.2) сводится к более простому, - это обучение молодого Ω. При этом оператор сети N все еще мал по сравнению с χ^-1I, и, следовательно, z_k в (6.5.2) можно заменить на χy_k. Это означает, что приращения N-процесса будут пропорциональны внешним произведениям y(t)y^T(t), за исключением экспоненциального затухания, вызванного забыванием. Ниже мы часто будем иметь дело с обучением в процессе развития- либо при изучении систематической долгосрочной модификации (с членом Е[yy^Т]), либо при рассмотрении реальной долгосрочной модификации (с членом yy^T).

Мы нуждаемся также в допущении о способе "запуска" памяти Ω в момент времени t = 0 и будем пользоваться выводами, полученными в разд. 6.3 для сетей с высокой степенью расхождения.

Аксиома М2. Мы считаем, что исходная сеть осуществляет только тривиальную обработку информации в том смысле, что в нулевой момент времени N пропорционален тождественному N (0) = εI.

В разд. 6.3 было установлено, что спектр случайно инициированной сети 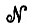обладает при определенном значении, скажем λ_max, точкой отсечки. В таком случае естественнее предполагать лишь выполнение условия N (0) ≤ λ_maxI, т. е. равенство в аксиоме М2 следует заменить неравенством с ε = λ_max. Недавно Дж. Силверстайн показал, что для дальнейшего анализа строгое равенство действительно не требуется.

Если сеть обладает высоким расхождением, то из теоремы (6.3.1) следует, что спектр концентрируется вокруг определенного значения, и в аксиоме М2 можно постулировать равенство.

Если Ω живет в некоторой стационарной среде, то что произойдет с его отображением памяти при предъявлении его exp (Ω)? Сходится ли оно к насыщенному отображению памяти и если да, то каковы его взаимосвязи со средой?

Для того чтобы уяснить это, рассмотрим уравнение

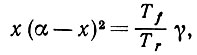
роль которого станет понятна ниже (здесь использовано обозначение χ^-1 = α). Обозначим через x^γ наименьший положительный корень этого уравнения. Нетрудно убедиться в том, что при

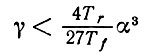
x_γ < α/3, а в противном случае x_γ > (4/3)α. Обозначим соответствующую функцию через Н: γ → x_γ. Следует отметить, что эта функция имеет разрыв при

(см. рис. 6.5.1.)

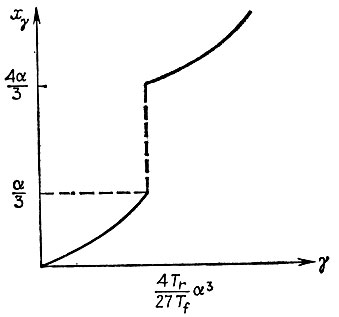
Рис. 6.5.1

Предложение 6.5.1. Рассмотрим некоторую стационарную среду exp (Ω) с оператором опыта Γ. Если

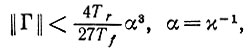(6.5.3)

то при малых ε (на самом деле нам требуется всего лишь ε < α/3) отображение памяти сходится к некоторому нормальному насыщенному пределу, определяемому как

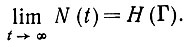(6.5.4)

Замечание. Правая часть (6.5.4) имеет значение, которое обычно придается функциям ограниченных симметрических операторов (см., например, Халмош (1951), с. 37).

Доказательство. Для вычисления первого члена правой части уравнения (6.5.2) сформируем выражение

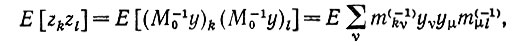(6.5.5)

где

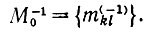
Используя определение оператора опыта Γ,

получаем, что

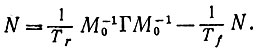(6.5.6)

и, следовательно, уравнение (6.5.2) можно переписать в матричной форме

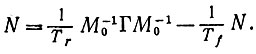(6.5.7)

Приводим к диагональной форме ковариационную матрицу

Γ = Θ^TΓ'Θ, где Γ' имеет диагональные элементы γ₁, γ₂, ..., самое большее равные

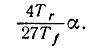
Мы покажем, что отображение памяти в момент времени t представляет собой

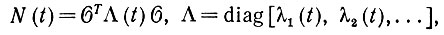(6.5.8)

где λ_υ(t) будут вскоре определены.

Введем дифференциальное уравнение

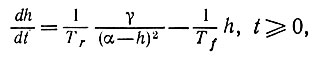(6.5.9)

с начальным условием h(0) = ε > 0. Решение будем обозначать через h(t, γ). Очевидно, что

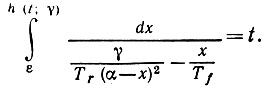(6.5.10)

Числитель в подынтегральном выражении положителен, если x заключен между ε и наименьшим значением x_γ, при котором выполняется соотношение

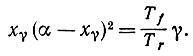(6.5.11)

Функция x(α - x)² имеет максимум (4/27)α³ при x = α/3, так что на основании неравенства (6.5.3) получаем, что x_γ < α/3. Интеграл (6.5.10) претерпевает логарифмический рост при x = x_γ, и, следовательно,

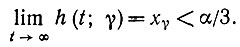(6.5.12)

Теперь мы покажем, что решение определяется (6.5.8), где

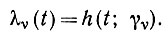(6.5.13)

Действительно, при t = 0 мы получаем, что _υ(0) = ε, и, следовательно, N(0) = εI, как и требовалось. Кроме того, поскольку соответствующая матрица

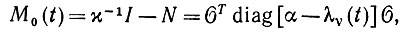(6.5.14)

мы получаем

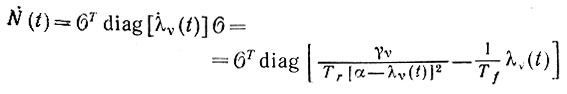(6.5.15)

и, воспользовавшись (6.5.14),

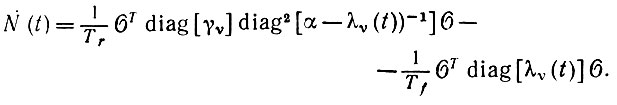(6.5.16)

С учетом (6.5.8) это сводится к

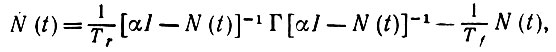(6.5.17)

так что N (t) удовлетворяет аксиоме модификации (см. уравнение (6.5.7)).

Устремив в (6.5.14) t к бесконечности, получаем насыщенное отображение памяти

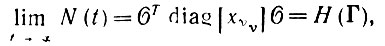(6.5.18)

как и утверждалось, на чем доказательство завершается.

Отметим, что, поскольку x_γυ < H М₀( + ∞) = αI - N(+ ∞) неотрицательно определенный. Если собственное значение γ_υ = 0, то, поскольку h (+ ∞, 0) = 0, соответствующее значение x₀ = 0. Следовательно, независимо от того, является оператор Γ определенным или нет, насыщенное отображение памяти М( + ∞) положительно определено в подпространстве, стягиваемом оператором Γ. Другими словами, насыщенное отображение памяти устойчиво в exp(Ω).

Этот результат позволяет нам выдвинуть качественное утвержден, описывающее связь долгосрочной памяти со стационарной средой.

Предложение 6.5.2. Если существо Ω живет в стационарной среде exp (Ω), причем

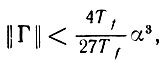
то насыщенное отображение памяти N (+ ∞), существование которого гарантируется предложением 6.5.1, имеет некоторое подпространство сознательной сферы, равное пространству, стягиваемому оператором Γ.

Доказательство. Из (6.5.18) следует, что собственные векторы N(+ ∞) соответствуют собственным векторам Γ, поскольку они одновременно были подвергнуты диагонализации с помощью одного и того же ортогонального преобразования Θ. Но всякое собственное значение N (+ ∞) равно нулю тогда и только тогда, когда соответствующий собственный вектор Γ также имеет нулевое собственное значение. При этом N(+ ∞) и Γ стягивают одно и то же подпространство, как и утверждалось.

Отсюда непосредственно получаем:

Следствие. При выполненных условиях предложения 6.5.2 подпространство сознательной сферы содержит некий элемент, соответствующий признаковому пространству φ^υ_j υ-го признака, если exp (Ω) удовлетворяет следующему условию:

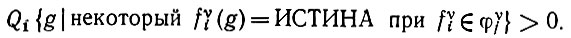(6.5.19)

Доказательство. Если условие (6.5.19) выполнено, то используется предложение 6.2.7. Из (6.5.19) следует, что коэффициент проецирования в φ^υ_j не равен нулю, а это означает, что пространство, стягиваемое оператором опыта, должно содержать элемент этого признакового пространства.

Роль параметра ε исходной памяти заслуживает специального комментария. Предполагается, что оператор исходной сети тривиален - он просто пропорционален единичной матрице N (0) = εI (см. аксиому М2), где ε - некоторое малое положительное число. Если исходной служит некоторая другая малая матрица, то доказательство предложения 6.5.1 теряет силу, если эту матрицу нельзя диагонализировать совместно с оператором Γ. Можно, однако, все еще утверждать, что единственное предельное отображение памяти должно иметь вид, определяемый (6.5.18).

На предложение 6.5.1 не следует возлагать чрезмерных надежд: оно не гарантирует, что отображение памяти насыщается всегда. В самом деле, внешне безобидное условие (6.5.3) играет существенную роль и без него память разрывается.

Предложение 6.5.3. При некоторой стационарной среде с оператором опыта Γ, таким, что

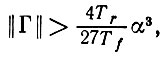(6.5.20)

отображение памяти становится неустойчивым в критический момент времени t = t_crit

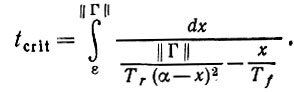(6.5.21)

Доказательство. При указанном условии, по крайней мере, одно из собственных значений Γ больше значения правой части I .5.20); пусть этим значением будет γ₁. Оператор сети, определяемый (6.5.8) и (6.5.13), все еще служит решением при малых значениях t, что можно доказать так же, как и выше. Однако при увеличении t ситуация меняется, как можно убедиться, рассмотрев функцию h(⋅, γ₁). Знаменатель интеграла (6.5.10) теперь положителен по крайней мере вплоть до значения x = α. Следовательно, значение функции h(t, γ₁) будет превышать значение а при t → +∞. При этом отображение памяти M₀(t) = αI - N (t) перестает быть определенным, и поэтому возникает переход к неустойчивой памяти, как и утверждалось в доказываемой теореме. Момент возникновения этой неустойчивости tx определяется про-хождением функции h(t₁, γ₁) через значение а, так что

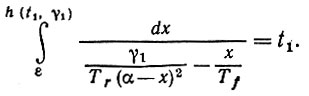(6.5.22)

Этот результат получен для собственного значения γ₁ оператора Γ. Рассмотрим теперь все собственные значения и наименьшее значение t (в соответствии с (6.5.21)). Это означает, что наибольшее собственное значение max _υ ||Γ|| определит критический момент времени, и тем самым наше предложение доказано.

В пространствах Y и ω мы с самого начала использовали обычную евклидову норму. По мере модификации сети изменяется геометрия пространства Z, и известно, что соответствующее внутреннее произведение определяется в Z как

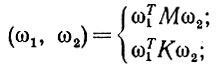(6.5.23)

выбор в этом определении зависит от того, рассматриваем ли мы ответ в собственно установившемся режиме или отклонение от реакции не модифицированной сети.

В любом случае существенно то, что в рамках аксиоматического подхода к процессам мышления обучение представляет собой изменение геометрии в пространстве состояний.

Выше мы часто имели дело с ортогональностью. Представляет определенный интерес то обстоятельство, что некоторые из этих ортогональностей фиксированны, т. е. имеют анатомическую природу. Так обстоит дело, например, с подпространствами U^υ. С другой стороны, существует ортогональность между пространствами М и K. Эти пространства размещаются в некотором абстрактном пространстве высокой размерности, а не в физическом пространстве, причем возникает эта ситуация в результате обучения, но не задается при рождении.

Прежде чем закончить с темой модификации сети , рассмотрим кратко роль случайности в поступлении входных векторов в сеть. Полное исследование этой проблемы, которое вне всякого сомнения было бы весьма целесообразным, придется пока отложить.

Мы будем считать, что на протяжении интервала времени (t, t + h) вклад матрицы {y_ky_l} будет равен

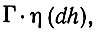(6.5.24)

где η -некоторый вероятностный процесс с независимыми приращениями, распределенными в соответствии с Γ-распределением. Последнее не лишено смысла, поскольку мы имеем дело с квадратами и произведениями переменных y. Если, в частности, y - фиксированный вектор, умноженный на случайную величину, подчиняющуюся нормальному распределению, это предположение будет естественным.

Большие сомнения, чем допущение о виде распределения, вызывает условие пропорциональности приращений Γ. Мы сделаем по этому поводу несколько замечаний после доказательства следующего предложения.

Предложение 6.5.4. Приняв допущение (6.5.24), при малой ||Γ|| получаем приближение первого порядка для распределения N (∞) в следующем виде:

(i) вся вероятность сосредоточена в корнях уравнения

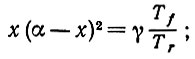(6.5.25)

(ii) приближение второго порядка плотности распределения вероятностей:

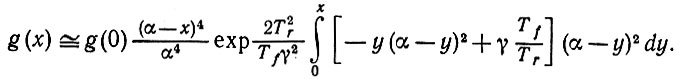(6.5.26)

Доказательство. Первый член в правой части стохастического дифференциального уравнения (6.5.2) пропорционален γ_kl - элементу матрицы Γ. Эта пропорциональность постоянна - одна и та же для всех k и l, но изменяется случайным образом во времени в соответствии с описанным выше распределением. Это означает, что N (t) будет иметь вид (см. уравнение (6.5.8))

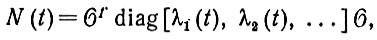(6.5.27)

где n_i(t) который марковский процесс, удовлетворяющий стохастическим дифференциальным уравнениям с разделенными переменными:

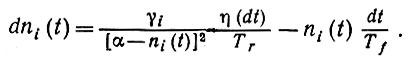(6.5.28)

Проведем анализ при некотором фиксированном i и, чтобы упростить обозначения, опустим этот индекс. Процесс, определяемый (6.6.28), обладает независимыми приращениями, подчиняющимися Γ-распределениям, и потому плотность распределения вероятностей процесса η(h) равна

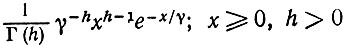(6.5.29)

и

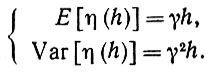(6.5.30)

Если G - равновесная функция распределения (6.5.28) и φ(z)- соответствующая характеристическая функция, то факт одинаковости характеристических функций n(t) и n(t + h) можно при малых h представить следующим образом:

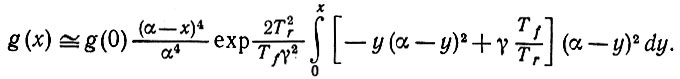(6.5.31)

Здесь в подынтегральном выражении член - (xh/T_f) соответствует члену, представляющему экспоненциальное затухание в (6.5.28). Выражение в квадратных скобках - это характеристическая функция первого члена в (6.5.28), представленная в виде известного преобразования Фурье от Γ-распределения.

Пусть теперь приращение времени h стремится к нулю в уравнении (6.5.31). Тогда с учетом только члена первого порядка по h получаем, что

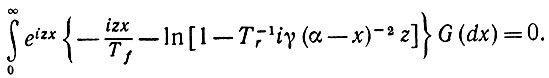(6.5.32)

При очень малых значениях z мы разлагаем функцию логарифма, сохраняя только линейный член, и получаем приближение первого порядка

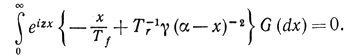(6.5.33)

Поскольку это уравнение должно быть справедливо при любых z, то вся масса G должна быть сосредоточена в точках x, являющихся решением уравнения

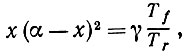(6.5.34)

которое мы уже изучали. Это, конечно, означает, что здесь мы возвращаемся к уже рассмотренной детерминистской ситуации.

Что происходит, когда z не так мало, уже менее очевидно. Приближение второго порядка (6.5.32) приводит к

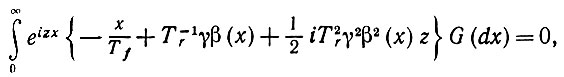(6.5.35)

где β(x) = (α - x)^-2. Интегрируя по частям третий член, получаем при G' = g

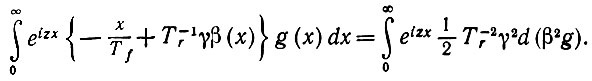(6.5.36)

Итак, мы получаем дифференциальное уравнение

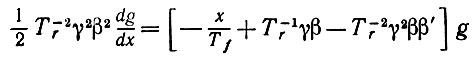(6.5.37)

или

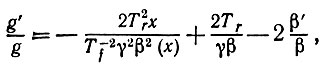(6.5.38)

решением которого является

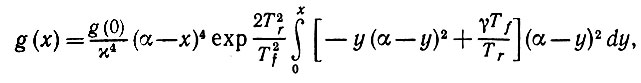(6.5.39)

а это и есть приближение второго порядка.

Отметим, что подынтегральное выражение обращается, в нуль при y = y₀, определяемом рассмотренным выше уравнением (6.5.25). Пусть γ в этом уравнении не слишком велико, так что первый корень y₀ < α. Плотность распределения g пропорциональна произведению (α - x)⁴ на некоторую показательную функцию подынтегрального выражения. Второй множитель увеличивается от x = 0 до x = y₀, после чего он монотонно убывает. Он стремится к нулю при x → ∞ исключительно быстро, потому что показатель степени равен 6. Первый множитель убывает от x = 0 до x = α и затем снова убывает вплоть до + ∞, причем очень медленно по сравнению со вторым множителем.

Объединяя это уравнение с (6.5.38), устанавливаем, что плотность распределения имеет максимум слева от y₀, быстро падает от нуля, соответствующего критическому значению y = α, а затем снова становится положительной и быстро уменьшается до нуля. Соответствующий график представлен на рис. 6.5.2.

Теперь достаточно просто напомнить, что норма ||N(t)|| определяет устойчивость сети . С помощью (6.5.39) можно вычислить вероятность того, что сеть устойчива, поскольку ||N(t)|| - это процесс n₁(t), рассмотренный выше.

Следует заметить, что результат, выражаемый этим предложением, основывается на эвристических соображениях и для обеих аппроксимаций нами не получены члены, характеризующие ошибки. Еще важнее то обстоятельство, что допущение (6.5.24) не совсем удовлетворительно.

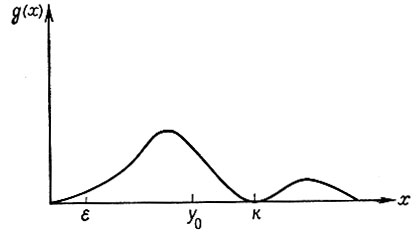
Рис. 6.5.2

Лучше было бы потребовать, чтобы вклад в стохастическое дифференциальное уравнение на временном интервале (t, t + h) определялся процессом Уишарта с h в показателе характеристической функции. В связи с этим следовало бы попытаться получить точно или приближенно распределение ||N(t)||, однако это еще не было сделано.

Как же можно охарактеризовать силу мыслительных способностей Ω и его способности обучаться? Конечно, m - физический размер сети - отражает их в какой-то степени, но более естественной мерой была бы, по-видимому, степень уплотнения μ при полном уплотнении или какой-либо иной числовой критерий, если уплотнение частичное. Действительно,μ определяет верхнюю грань сложности вывода, на реализацию которого Ω можно рассчитывать. Достижение этой верхней грани зависит, как мы убедимся в следующем разделе, от exp (Ω).

Другие сетевые параметры того же характера - это расхождение d сети и средняя связность (см. разд. 6.3), однако до сих пор мы не достигли полного понимания ситуации, когда все коэффициенты связи не поддаются модификации. В этом случае, несомненно, следует ожидать, что при реализации сетью обратной связи в соответствии с уравнением сети важную роль будет играть именно средняя связность.

Все эти критерии фиксированные. В отличие от них оператор N изменяется при обучении Ω, и критерии обучения должны отражать эволюцию этого оператора: величина типа

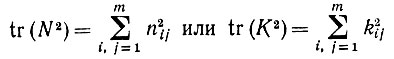(6.5.40)

представляется разумной, но пока мы не будем обсуждать этот вопрос более подробно.