1.1. Постановка и классификация задач. Общие понятия

Когда говорят о задачах математического программирования (планирования), то имеют в виду класс задач оптимизации, возникших в последние три десятилетия в связи с попытками повысить эффективность промышленных, транспортных, военных систем за счет улучшений в работе координирующих и управляющих органов. Несмотря на разнообразие смыслового содержания таких задач, все они с формальной точки зрения сводятся к одной общей постановке: найти значения переменных x₁, x₂, ...., x_n, доставляющие максимум (минимум) заданной скалярной функции z = f(x₁ ,..., x_n) при условиях

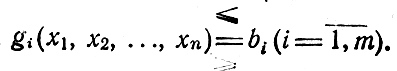
Условия, о которых идет речь, ограничивают выбор значений х₁, х₂,...., х_n и могут обладать самыми разнообразными свойствами, определяемыми видом функций g_i(x₁, х₂,..., х_n); в каждой из m строк здесь сохраняется какой-либо один знак (равенство, неравенство).

Введем ряд общих понятий, которые понадобятся в дальнейшем.

1. Совокупность различимых между собой объектов одинаковой природы принято называть множеством; каждый из таких объектов в отдельности есть элемент множества (принадлежность некоторого элемента множеству E обозначается как e ∈ E); в данном пособии речь будет идти о множествах, элементами которых являются математические объекты (числа, точки, функции и т. п.).

2. Множество E₁ представляет собой некоторое подмножество множества E (обозначается E₁∩E₂), если каждый элемент e, принадлежащий E₁, одновременно принадлежит и E; в случае, когда E₁ не содержит ни одного элемента (т. е. является пустым множеством, E₁ = ∅ ), оно может рассматриваться как подмножество любого множества E.

3. Пересечение множеств E₁ и E₂ (обозначается E₁∩E₂) есть множество всех элементов e, содержащихся и в E₁ и в E₂, объединение множеств и E₂ (обозначается E₁∪E₂) есть множество всех элементов e, содержащихся либо в E₁, либо в E₂, либо и в E₁, и E₁.

4. Множество E называется упорядоченным, если любые два его элемента e₁, e₂ связаны либо отношением e₁<e₂, либо отношением e₁>e₂ (таким свойством обладает, например, множество всех вещественных чисел); в этих условиях элемент ê называется верхней границей множества E, если ě≤e для всех e∈E, наименьший из имеющихся ê называется точной верхней границей (аналогично определяются нижняя и точная нижняя границы множеств).

5. Множество E называется метрическим пространством, если каждой паре его элементов e₁, e₂ поставлено в соответствие неотрицательное число (метрика) ρ(e₁, e₂), удовлетворяющее условиям: ρ(e₁, e₂) = 0 только при e₁ = e₂ (аксиома тождества), ρ(e₁, e₂) = ρ(e₂, e₁) (аксиома симметрии), ρ(e₁, e₂) + ρ(e₂, e₃) ≥ ρ(e₁, e₃) (аксиома треугольника).

6. Метрическое пространство, элементами которого являются упорядоченные системы из n вещественных чисел (x₁, x₂ ,..., x_n) = X, (y₁, y₂ ,..., y_n) = Y, а метрикой - расстояние

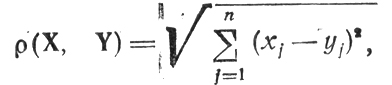
называется n-мерным эвклидовым пространством (обозначается R_n); элементы X, Y, ... могут рассматриваться как точки пространства R_n (или векторы в пространстве Rn), определяемые своими координатами x_j, y_j, ... (j = 1,...,n); величина

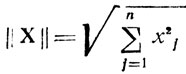
называется нормой или модулем вектора X; произведение вида ||Х||||Y||cos γ, где γ - угол между векторами X и Y называется скалярным произведением (X, Y) этих векторов.

7. Множество точек X∈R_n, для которых ρ(Х, Х₀)≤r, называется замкнутым шаром радиуса r с центром в точке Х₀; множество точек X∈R_n, для которых ρ(Х, Х₀)<r, называется открытым шаром с центром в Х₀.

8. Окрестностью произвольной точки Х∈R_n называется любой открытый шар с центром в этой точке.

9. Подмножество R̄_n множества R_n называется ограниченным, если оно содержится в (некотором замкнутом шаре S(r, X₀)⊂R_n; диаметром множества R̄_n в пространстве R_n называется точная верхняя граница расстояний между любыми двумя точками Х₁, X₂∈R̄_n.

10. Точка X_Π∈R_n называется пределом последовательности точек X_k, принадлежащих R_n, k = 1, 2, .. если ρ(X_k, Х_Π) → 0 при k → ∞.

Заметим теперь, что множество точек X, удовлетворяющих системе ограничении

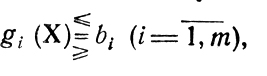
есть область определения (U) поставленной выше задачи. Функция z называется целевой функцией (в конкретных исследованиях это - критерий эффективности технической системы, показатель качества производственного плана и т. п.); она достигает своего экстремального значения в одной или нескольких точках области U, которые нужно искать.

Обычно вид функций z к g_i (i = 1,..., m) известен, константы b_i заданы, величины тип являются произвольными целыми числами (в отдельных случаях между ними устанавливается отношение вида m<n). Специально оговариваются ограничения, выраженные в требованиях не отрицательности и целочисленности переменных x_j (j = 1,...,n).

Сделанные замечания позволяют дать краткую символическую запись условий задачи математического программирования:

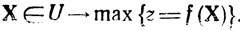
В основу существующей классификации таких задач положены особенности функций z или g_i, встречающихся в конкретных практических исследованиях. Различают два основных класса задач математического программирования - задачи линейного и нелинейного программирования. К первым относятся такие, в которых и целевая функция, и все функции g_i (i = 1,...,m) линейны относительно переменных x_j (j = 1,..,n), т. е.

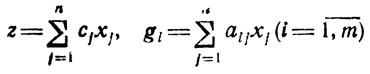
(здесь c_j и a_ij - известные постоянные коэффициенты). Из дополнительных ограничений обычно вводится требование ∀x_j ≥ 0 (j = 1,...,n). Если к тому же поставлено условие "все (или некоторые) x_j - целые числа", возникает задача целочисленного линейного программирования; методы ее решения имеют свои характерные особенности.

Во всех других случаях говорят о задачах нелинейного программирования. Чтобы не перечислять их многочисленные признаки, обратим внимание на следующее. В настоящее время хорошо изучены и довольно широко распространены задачи:

- решаемые методами классической математики при условии, что среди ограничений нет неравенств и m<n, нет требований не отрицательности или целочисленности переменных, функции z и g_i непрерывны и по крайней мере дважды дифференцируемы;

- с линейными ограничениями и целевой функцией вида

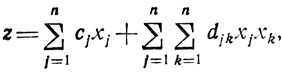
- с сепарабельной целевой функцией

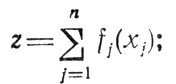
- обладающие такими универсальными свойствами, как выпуклость z и U, что позволяет формировать и использовать условия существования решений независимо от конкретных форм задания z и g_i (i = 1,...,m).

Приведенная классификация условна, поскольку она охватывает лишь задачи с полной информацией (т. е. такие, с которых все определено); кроме них можно указать целые группы задач, содержащих различные неопределенности (случайность отдельных параметров, отсутствие сведений о виде целевой функции и т. д.), следствием чего является практически неограниченное разнообразие приемов решения, позволяющих собрать и эффективно использовать недостающую информацию. Все это нашло отражение в материалах и структуре разделов книги, подчеркивающих важность существующих проблем оптимизации для различных областей целенаправленной деятельности.

Обратимся теперь к определениям экстремума, имея в виду безусловный абсолютный максимум (минимум), безусловный относительный максимум (минимум), условный абсолютный максимум (минимум) и условный относительный максимум (минимум).

Пусть в оптимизационной .задаче нет условий-ограничений (m = 0, отсутствуют ограничения вида x_j - целые числа) и целевая функция z = f(X) определена на множестве R_n. В этом случае говорят, что f(X) имеет безусловный абсолютный (глобальный) максимум в точке X^*, если f(X)≥f(X) для всех X∈R_n. Изменив здесь знак неравенства на противоположный, приходим к определению безусловного абсолютного минимума f(X). Таким образом, точка X^* как бы доминирует над всеми остальными точками пространства R_n, доставляя функции f(X) экстремальное значение.

Нетрудно представить, что могут существовать и такие точки (назовем их X°), которые доминируют в указанном смысле лишь над соседними, довольно близко лежащими точками; с существованием Х° связано понятие относительного (или локального) экстремума.

Пусть по-прежнему в задаче нет никаких ограничений и функция z = f(X) определена на множестве R_n. Рассмотрим множество точек X, составляющих окрестность (хотя бы достаточно малую) некоторой точки Х°. Если для всех этих X справедливо утверждение f(Х°)≥f(Х), то в точке Х° функция f(X) имеет безусловный относительный (локальный) максимум. Изменение знака неравенства на противоположный позволяет дать определение безусловного относительного минимума.

Если приведенные выше неравенства сделать строгими, то можно говорить о сильном экстремуме; в противном случае определяется слабый экстремум.

Рассмотренные виды экстремума редко встречаются на практике. Для любой задачи математического программирования характерно наличие более или менее жестких ограничений, придающих ей определенную специфику. В этом случае искомые экстремальные точки X^* или Х° должны обязательно принадлежать области U, поэтому сам экстремум называется условным.

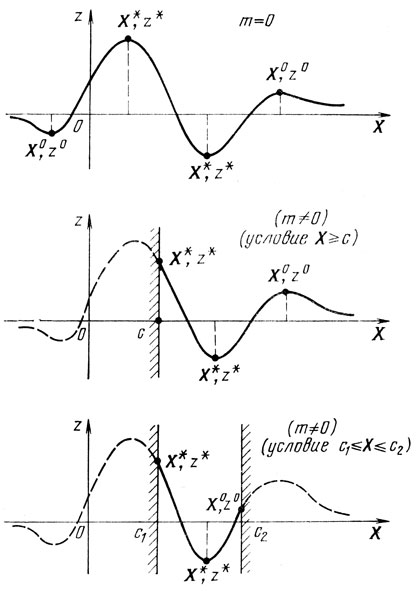
Рис. 1.1

Пусть дана задача математического программирования в общей постановке (см. стр. 8) и z = f(X) определена на R_n. В этом случае точка Х^*∈U является точкой условного абсолютного максимума z, если для всех X∈U выполнено f(Х^*)≥f(Х).

Наконец, функция f(X) имеет в Х°∈U условный относительный максимум, если неравенство выполнено для всех X, принадлежащих и области U, и некоторой окрестности точки Х°.

Изменив здесь знаки неравенств, можно получить соответствующие определения условного минимума z или, рассмотрев только строгие неравенства, сформулировать понятия сильного условного экстремума и т. д. Дополнительные пояснения дает рис. 1.1, иллюстрирующий приведенные определения.

Чтобы закончить обсуждение общих вопросов, обратим внимание на следующее: с формальной точки зрения нет необходимости различать задачи поиска максимума и минимума, так как одна задача сводится к другой изменением знака z; принятые обозначения (X^* и Х°) точек абсолютного и относительного экстремума будут сохранены в дальнейшем, соответствующие им значения z есть z^* и z°; из рис. 1.1 следует, что точек Х° (и даже X^*) может быть несколько и что Х:,: является одновременно точкой локального экстремума; это дает основание искать X^* путем перебора Х° и сравнения имеющихся f(X°) (особенно тогда, когда применяемые методы решения задач позволяют получать лишь Х°).