1.2. Линейное программирование. Основные свойства задачи

Задача линейною программирования, как отмечалось выше, состоит в отыскании значений n переменных х₁, х₂, ...., х_n) доставляющих экстремум функции z = ⁿΣ_{j = 1} c_jx_j при условиях

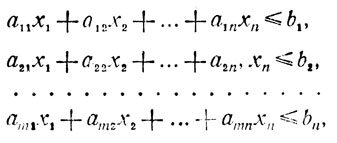(1.1)

представляющих собой систему линейных нестрогих неравенств, которые в случае необходимости могут быть превращены в равенства посредством присоединения искусственных переменных x_n+i:

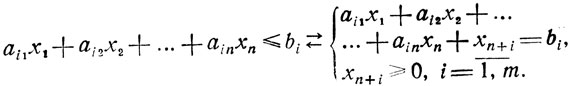
Подобная операция приводит к увеличению размерности задачи и появлению дополнительного требования не отрицательности x_n+i, однако часто это единственный путь получить решение.

Форма записи ограничений (1.1) является достаточно обшей, хотя сюда обычно добавляется условие ∀x_j≥0 (в противном случае нужно иметь m>n). Полезно заметить, что включение в (1.1) хотя бы одного строгого неравенства осложняет решение задачи; например, если z = x₁ и x₁ < 1, то нельзя указать значение x₁ которое доставило бы максимум z.

Свойства решений задачи линейного программирования во многом зависят от особенностей области определения, заданной неравенствами (1.1). Для изучения этих свойств введем следующие понятия:

- отрезком, соединяющим две данные точки X₁, Х₂, называется множество точек X с координатами x_j = ax_j1 + (1 - a)x_j2 (0 ≤ а ≤ 1, j = 1,...,n), где x_j1, x_j2 - координаты точек X₁ и Х₂ соответственно; а - изменяемый параметр, определяющий положение X (нетрудно видеть, что при а = 1 точка X совпадает с Х₁ а при а = 0 - с Х₂);

- произвольная область называется выпуклой, если вместе с двумя любыми точками она содержит и весь отрезок, соединяющий эти точки (часто слово "область" заменяют словом "множество", вкладывая в него тот же смысл);

- множество точек X, координаты которых удовлетворяют неравенству вида a₁x₁ + a₂x₂ +...+ a_nx_n ≤ b называется замкнутым (т. е. содержащим собственную границу) полупространством (оно обладает свойством выпуклости);

- точка X, принадлежащая выпуклой области, называется крайней, если в данной области нет двух таких точек Х₁≠X₂, что x_j - ax_j1 + (1 - a)x_j2 при 0 < а < 1 (крайняя точка не может находиться на отрезке между X₁ и Х₂, принадлежащими той же области).

Приведенные определения иллюстрирует рис. 1.2. Легко заметить, что система неравенств (1.1) указывает в R_n область U, являющуюся пересечением m замкнутых полупространств (т. е. выпуклым многогранником). Это подтверждает и рис. 1.3, где показана область U, определяемая условиями -x₁ + x₂ ≤ 1; -х₁ - x₂ ≤ 0; x₁ ≤ 3. С увеличением числа переменных наглядность геометрических представлений теряется, однако аналогии с рассматриваемым примером сохраняются полностью, и в дальнейшем область определения линейной задачи будет условно изображена так, как показано на

рис. 1.4. Полезно заметить, что вершины выпуклого многогранника U являются крайними точками, причем их число конечно.

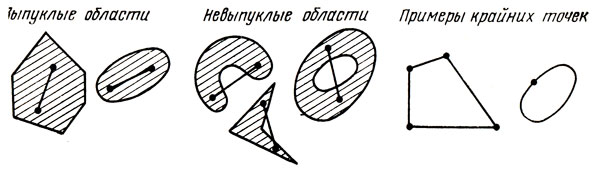
Рис. 1.2

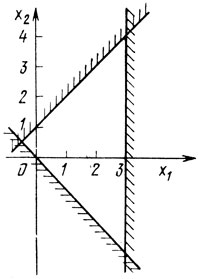
Рис. 1.3

Обратимся теперь к следующей теореме (1): экстремум целевой функции в задаче линейного программирования (если он существует) всегда является абсолютным.

Доказательство: пусть для определенности экстремум z есть максимум, и в U все-таки

существует точка Х° (рис. 1.5) с координатами х°₁, х°₂, ....,х°_n. Предполагая таким образом наличие локального максимума z, необходимо допустить и существование в U некоторой точки X̄, где значение z больше, чем z° = f(X°) (иначе величину z° надо было бы признать абсолютным максимумом z). Рассмотрим отрезок, соединяющий Х° с X̄. В любой его точке X, заданной координатами x_j = ax̄_j + (1 - a)x°_j (0 < a <1, j = 1,..,n), целевая функция 14 принимает значение z = f(X) = ⁿΣ_{j = 1} c_j(ax̄_j + [1 - a)x°_j] = af(X) + (1 - a)f(X°) или f(X) = a[f(X) - f(X°)] +f(X°).

Поскольку f(X) - f(X°) > 0 (исходное допущение), значения f(X) непрерывно возрастают с увеличением а от 0 до 1. Другими словами, f(X) > f(X°), даже если X при надлежит достаточно малой окрестности Х°; но это противоречит утверждению о том, что z имеет в Х° локальный максимум. Следовательно, в У не может быть точек Х°, отличных от Х^*.□

Рис. 1.4

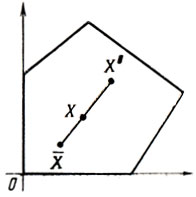
Рис. 1.5

Теперь можно говорить о множестве {X^*} глобально оптимальных решений (точек) X^*, допуская, что в каких-то случаях оно содержит один элемент, в каких-то более одного, а иногда вообще является пустым.

Другое важное свойство линейных задач отражено в теореме (2): множество точек X^* в задаче линейного программирования (если оно не пусто) всегда содержит хотя бы одну крайнюю точку многогранника U.

Доказательство: пусть число элементов множества {X^*} больше единицы, и среди точек X^* нет ни одной крайней точки многогранника U. Это значит, в U можно найти такие две различные точки Х₁, Х₂, что произвольно взятая точка Х^*∈{Х^*} окажется на соединяющем их отрезке, и тогда f(X^*) = [f(X₁) - f(X₂)]a^* + f(X₂). Очевидно, рассматриваемое равенство должно существовать совместно с требованиями f(X^*) ≥ f(X₁) и f(Х^*) ≥ f(Х₂), вытекающими из определения абсолютного экстремума (для определенности - максимума), однако достичь этого удается лишь при f(X₁) = f(X₂) = f(X^*) (проверку можно осуществить непосредственной подстановкой выражения f(X^*) в оба указанных выше неравенства). Таким образом, из исходных предположений следует вывод о принадлежности X₁, Х₂ множеству {X^*}, причем этот вывод относится к любым Х₁, Х₂, допустимым по условию построения отрезка, содержащего выбранную точку X^* (в частности, к любым точкам этого отрезка). Заметим теперь, что указанными свойствами могут обладать лишь точки, находящиеся на границе многогранника U (если бы X^* оказалась внутренней точкой, было бы нетрудно нарушить условие f(X₁) = f(X₂) = f(X^*), построив прямые, лежащие в разных плоскостях; см. рис. 1.6). Следовательно, множество {X^*} является либо гранью, либо ребром выпуклого многогранника, но в таком случае оно обязательно содержит хотя бы одну крайнюю точку, которая может рассматриваться как экстремальная.

Сделанные замечания легко переносятся на случай, когда {X^*} содержит всего один элемент - единственную точку X^*. Здесь равенства f(X₁) = f(Х₂) = f(Х^*) означают совпадение Х₁, Х₂, X^*, вследствие чего необходимо признать X^* крайней точкой U.

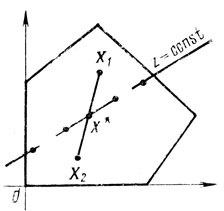
Рис. 1.6

Чтобы использовать полученные геометрические представления, нужно дать их формальную интерпретацию и построить на этой основе метод решения рассматриваемых задач.