1.4. Симплекс-алгоритм. Принцип организации переходов

Пусть задача линейного программирования дана в следующей постановке: найти значения x₁ ≥ 0, x₂ ≥ 0,..., x_n ≥ 0 доставляющие минимум функции z = ⁿΣ_{j = 1} c_jx_j при

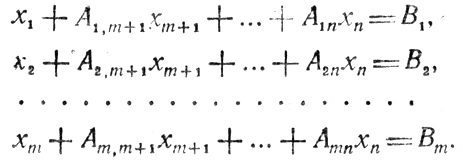(1.9)

Считая каноническую форму (1.9) допустимой рассмотрим очевидное базисное решение (∀∀B_i≥0) x₁ = B₁, ...., x_m = B_m, x_m+1 = ... = x_n = 0. Ответ на вопрос, является ли оно оптимальным, можно получить, проведя несложные преобразования выражения z.

Умножим каждую строку (1.9) на коэффициент c_j, номер которого совпадает с номером этой строки, что позволяет прийти (после суммирования строк) к равенству z = z₀ + ⁿΣ_{j = m+1} c̃_jx_j где z₀ - некоторая константа; c̃_j - коэффициенты при свободных переменных рассматриваемого базисного решения. По своему смыслу z₀ есть значение z, получаемое в точке с координатами x₁ = B₁ = ,..., x_m = B_m, x_m+1 = .... = x_n = Очевидно, z₀ и все c̃_j определяются теми A_ij, В_j (i = 1,...,m; j = m + 1,...,n), которые присутствуют в (1.9), а также теми c_j (j = 1,...,m), которые входят в первые m слагаемых исходного выражения z.

Обратимся теперь к теореме (4):допустимое базисное решение x_i = В_i (i = 1,...,m), x_j = 0 (j = m + 1,....,n) является оптимальным тогда, когда коэффициенты c_j при не базисных переменных в выражении z = z₀ + ⁿΣ_{j = m+1} c̃_jx_j не отрицательны.

Доказательство: обратим внимание на то, что в предлагаемой задаче нужно минимизировать z и что z - z₀ = ⁿΣ_{j = m+1} c̃_jx_j. Если c̃_m+1 ≥ 0,...,c̃_n ≥ 0 то при любых x_j ≥ 0 (j = m + 1,..,n) разность z - z₀ не отрицательна, т. е. ее минимум есть 0. Следовательно, минимум z не будет меньше (иначе найдется отрицательное значение разности z - z₀, равное min z = z₀, а этого не должно быть). Для рассматриваемого базисного решения z = z₀, поэтому предыдущее утверждение можно сохранить, положив min z = z₀, что и доказывает теорему.□

Из проведенного доказательства следует: всякое решение системы (1.9), которому соответствует нулевая сумма c̃_m+1x_m+1 +...+ c̃_nx_n при ∀c̃_j≥0 и ∀x_j≥0 (j = m + 1,..., n), также будет оптимальным. Наконец, допустимое оптимальное базисное решение окажется единственным, если ∀c̃_j>0 (в этом случае свести к нулю разность z - z₀ можно, лишь приняв х_m+1 = ... = х_n = 0).

Таким образом, получен признак оптимальности решения линейной задачи, однако ясно, что сразу найти такое решение удается далеко не всегда. Даже в тех случаях, когда задача сведена к допустимой канонической форме, очевидное базисное решение чаще всего оказывается промежуточным и должно быть заменено новым, позволяющим получить лучшее (т. е. более близкое к оптимальному) значение z.

Пусть базисное решение вида x₁ = В₁, х₂ = В₂, ... .. ,х_m = В_m, x_m+1 = .... = х_n = 0 оказалось не оптимальным (среди коэффициентов c̃_j j = m + 1,...,n, есть отрицательные) . Чтобы перейти к другому допустимому решению, нужно сделать строго положительной (ввести в базис) какую-то из переменных x_m+1,...,x_n обратив в нуль одну из x₁, x₂,...,x_n Имея в виду ограничение ∀x_j≥0, можно сказать, что при таком переходе z уменьшится только тогда, когда вводимая переменная будет иметь в выражении z отрицательный коэффициент.

Обозначим через р тот номер j из {m+1,..., n}, для которого величина c_j, во-первых, отрицательна и, во-вторых, максимальна по модулю, т. е. c̃_p = min{c̃_j < 0}. Решив дать положительное приращение величине х_р = 0, представим базисные переменные иге помощью (1.9) в виде

Поскольку c̃_p < 0, нужно как можно больше увеличивать хр в стремлении минимизировать z, однако возрастание х_р будет продолжаться до тех пор, пока какая-то из переменных x₁, х₂,...,х_m не обратится в нуль. Это произойдет, если хотя бы один коэффициент A_ip (i = 1,...,m) в (1.10) положителен (по исходному условию В_i ≥ 0). Если же A_ip > 0 для нескольких номеров i из {1, 2,...,m}, то первой в нуль обратится та базисная переменная из (1.10), которой отвечает наименьшая величина отношения B_i/A_ip Таким образом, предельное значение x_р, до которого можно увеличивать x̂_р, найдется как x̂_p = min_i{B_i/A_ip}. Необходимо подчеркнуть, что равенство нулю хотя бы одного B_i при соответствующем A_ip > 0 (случай вырожденного базисного решения) означает невозможность ввода x_р в базис с соблюдением требований ∀x_j ≥ 0.

Указанная процедура перехода может быть повторена, если новое базисное решение допускает дальнейшее улучшение z. Симплекс-алгоритм состоит в последовательных повторениях подобных операций до тех пор, пока не будет найдено либо оптимальное решение исходной задачи линейного программирования, либо множество допустимых ее решений, для которых |z| → ∞ Полезно обратить внимание на то, что рассмотренный процесс поиска X^*, z^* закончится за конечное число шагов, если ни на одном из них не возникают вырожденные базисные решения.

Обратимся теперь к более подробному описанию этапов реализации симплекс-метода применительно к стандартной форме (1.2) условий задачи линейного программирования. Без потери общности можно считать здесь все b_i ≥ 0 (i = 1,...,m) (в противном случае достаточно умножить на -1 обе части соответствующих строк).

Этап I: система (1.2) искусственно расширяется путем введения переменной x_n+i ≥ 0 в i-ю строку (i = 1,...,m) и принимает вид

Если существует решение исходной системы (1.2), то оно допустимо и для (1.11) при x_n+1 = ... = x_n+m = 0; наоборот, если удастся получить решение (1.11), содержащее нулевые x_n+i (i = 1,...,m), то оно будет допустимым для (1.2);

- рассматривается сумма

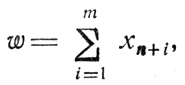
наименьшее возможное значение которой есть нуль вследствие не отрицательности x_n+1 именно оно будет достигнуто, если (1.2) имеет решение, причем проверка достижимости min w = 0 осуществляется в рамках следующей вспомогательной задачи линейного программирования: найти x_j ≥ 0 (j = 1,...,n), x_n+i ≥ 0 (i = 1,...,m)

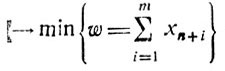
- решается задача минимизации w с использованием стандартного симплекс-алгоритма; в качестве начального базисного решения, как это следует из (1.11), принимается x_j = 0 (j = 1,...,n), x_n+i = b_i (i = 1,...,m). Если окажется min w > 0, то процесс вычислений можно прекратить, так как исходная задача с условиями (1.2) неразрешима; если же min w = 0, то соответствующее базисное решение фиксируется и используется на втором этапе исследований.

Таким образом, этап I предполагает предварительный анализ исходной системы уравнений (1.2) с целью указать для нее допустимое базисное решение (без вмешательства исследователя), если, конечно, таковое существует. В тех случаях, когда условия задачи представлены сразу в допустимой канонической форме, подобные действия оказываются излишними.

Этап II: оценивается решение вспомогательной линейной задачи, полученное в конце этапа I; в лучшем случае оно является невырожденным и содержит все x_n+i в числе свободных переменных; в худшем случае некоторые x_n+i войдут в базис (вырожденность), и тогда необходимо начинать этап II, сохраняя их нулевые значения; пусть в рассматриваемом решении свободными оказались x_j(j∈J₁, J₁ ⊂ {1, 2, ..., n}) и x_n+i (i ∈ J₂, J₂ ⊂ {1, 2, ...,m}), причем выражение w через эти переменные имеет вид

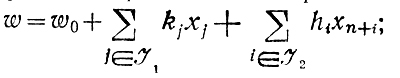
коэффициенты k_j,h_i здесь неотрицательны, поскольку речь идет об оптимальном решении, доставляющем min w = 0; чтобы на любом шаге этапа II сохранить w = 0, достаточно отбросить те x_j, x_n+i (j∈J₁, i∈J₂), которые имеют k_j, h_i > 0 в приведенном выше выражении w и сосредоточить внимание на оставшихся x_j, x_n+i с нулевыми коэффициентами k_j, h_i; решениям, состоящим только из таких x_j, x_n+i, всегда соответствует w = 0, что допустимо;

- после отбрасывания указанных x_j, x_n+i в рассмотрение вводится z и решается исходная задача линейного программирования; в результате либо отыскивается совокупность значений х^*₁, х^*₂,...,х^*_n, доставляющих экстремум z, либо обнаруживается, что |z| → ∞.

Ниже дан пример, иллюстрирующий возможности симплекс-метода.

Пример: найти x₁, х₂, ...,х₆ → min {z = -7х₁ - 5х₂} при

Решение: для простоты задача представлена сразу в канонической форме (относительно х₃,..., х₆); очевидное исходное базисное решение есть х₃ = 19, х₄ = 13, х₅ = 15, х₆ = 18, х₁ = х₂ = 0 и z = -7х₁ - 5х₂; обе не базисные переменные x₁, х₂ входят в выражение z с отрицательными коэффициентами, причем первый из них больше по -модулю, и согласно рекомендациям § 1.4 переменную x₁ нужно вводить в базис; для этого выпишем с помощью (1) ряд соотношений: x₃ = 19 - 2х₁, х₄ = 13 - 2х₁, x₅ = 15, х₆ = 18 - 3x₁; при возрастании x₁ первой обратится в нуль величина х₆, поэтому новое базисное решение есть х₆ = 0, x₁ = 6, х₃ = 7, х₄ = 1, x₅ = 15, х₂ = 0; z = -42 + 7x₆/3 - 5х₂ (ему соответствует величина z = -42, предыдущему безисному решению отвечало z = 0).

В новом выражении z отрицательный коэффициент имеет только х₂, и теперь необходимо рассмотреть соотношения x₁ = 6 - х₆/3, х₃ = 7 - 3х₂, х₄ = 1 - х₂, x₅ = 15 - 3х₂, которые показывают, что увеличивать х₂ можно лишь до единицы (при этом х₄ обращается в нуль); следовательно, новое (третье по счету) базисное решение есть x₄ = 0, х₂ = 1, х₆ = 0, x₁ = 6, x₃ = 4, x₅ = -12, z = -47 + 5x₄ - х₆ (ему соответствует z = -47).

Теперь в выражении z отрицательный коэффициент имеет х₆; введем эту переменную в базис, используя соотношения

полученные, как обычно, из (I); здесь при увеличении х₆ в нуль обращается прежде всего x₃, поэтому четвертое базисное решение есть x₃ = 0, х₆ = 3, х₅ = 6, х₁ = 5, х₂ = 3, х₄ = 0, z = - 50 +4x₃/3 + 11x₄/4.

Нетрудно видеть, что найденное решение оптимально: не базисные переменные х₃ и х₄ входят в выражение z с положительными коэффициентами; таким образом, x^*₁ = 5, х^*₂ = 3, х^*₃ = 0, х^*₄ = 0, х^*₅ = 6, х^*₆ = 3, z^* = -50.