1.3. Обоснование симплекс-метода. Этапы его реализации

Очевидно, всякая процедура, предусматривающая направленный перебор крайних точек области определения задачи, должна привести к отысканию среди них X^*. Эта идея отражена в так называемом симплекс-методе, являющемся классическим (и наиболее проработанным) методом в линейном программировании. Он позволяет найти крайнюю точку области U и определить, является ли она точкой экстремума целевой функции

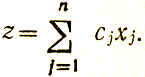
Если нет, то обеспечивается Переход в соседнюю крайнюю точку, где значение z больше (меньше) предыдущего, и тем самым делается шаг, приближающий получение решения. Через конечное число подобных шагов (обычно не более 2m) точка экстремума z либо оказывается найденной, либо признается несуществующей (например, в случае, когда ограничения задачи не совместны). Симплекс-метод является универсальным, так как позволяет решать задачу в общей постановке, хотя требует приведения ее к так называемому стандартному виду: найти х₁, х₂, ..., x_n доставляющие максимум (минимум) функции z ⁿΣ_{j = 1} c_jx_j при ограничениях

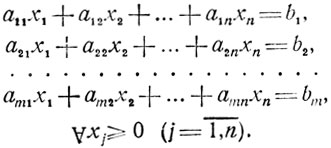(1.2)

Часто используется матричная форма представления рассматриваемых условий, например:

где A - матрица коэффициентов a_ij в (1.2); X и B - столбцы (х₁, х₂, ..., х_n) и (b₁, b₂, ..., b_m) соответственно, C - строка (c₁, c₂, ..., c_n).

Ограничения (1.2) представляют собой систему линейных неоднородных уравнений, решения которой определяют характер решения задачи в целом. Если система

(1.2) не имеет решений (множество U пусто), то задача теряет смысл; если существует единственное решение (1.2) (U содержит одну точку), то оно является одновременно и решением задачи, поскольку нет другого выбора; наконец, если система (1.2) имеет более одного решения, то рассматриваемая задача становится объектом исследования.

Известно, что в этом последнем случае искомое множество решений (1.2) может быть представлено как

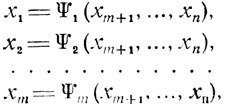(1.3)

где Ψ₁, Ψ₂,..,Ψ_m - линейные комбинации переменных x_m+1 ,...., x_n, называемых свободными. Вследствие линейности Ψ_i (i = 1,...,m) равенства (1.3) могут быть приведены к виду

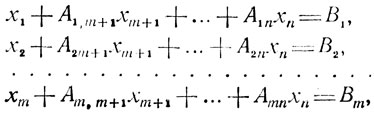(1.4)

причем (1.4) может рассматриваться как самостоятельная система уравнений, которой присуща следующая особенность: если номер j переменной x_j находится в пределах 1 ≤ j ≤ m, то эта переменная входит только в строку с номером i = j, имея при этом коэффициент, равный 1, и не входит в остальные m - 1 строк, для которых Такая система называется канонической.

Основным ее преимуществом является то, что она позволяет легко указать множество всех возможных решений системы (1.2), среди которых находятся так называемые базисные решения, представляющие собой интерес.

Частное решение системы (1.4), получаемое приравниванием свободных переменных x_m+1 ,..., x_n нулю, называется базисным; оно имеет вид

и является допустимым (с точками зрения требований ∀x_j≥0) при ∀B_i ≥ 0 (i = 1,..., m). Присутствие хотя бы одного B_i = 0 приводит к вырожденности рассматриваемого базисного решения (среди базисных переменных x₁, x₂, ..., x_m появляются такие, которые равны нулю).

Понятия, относящиеся к стандартной форме задачи линейного программирования, связаны с геометрическими представлениями, обсуждавшимися в § 1.2. В частности, существует соответствие между крайними точками множества U и решениями типа (1.5).

Пусть даны ограничения

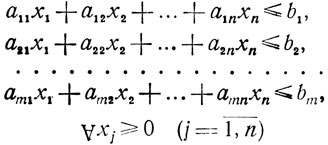(1.6)

или

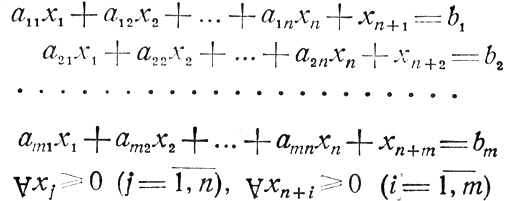(1.7)

с n свободными переменными х₁, х₂, ..., x_n (все b_i предполагаются строго положительными). Обратимся к теореме (3): допустимое базисное решение системы (1.7) определяет крайнюю точку области U, заданной неравенствами (1.6).

Доказательство: каждому набору значений х₁, х₂, ..., x_n (т. е. некоторой точке области U) соответствует набор х₁, х₂, ..., x_n, х_n+1, х_n+2, ..., x_n+m, представляющий собой допустимое решение системы (1.7); это следует из возможности однозначно определить базисные x_n+i (i = 1,...,m) через свободные x_j (j = 1,..,n). Пусть X₁ и Х₂ - точки в U с координатами x_j1, x_j2, а x_j1, x_n+i,1 и x_j , x_n+i,2 - соответствующие им решения (1.7). Рассмотрим произвольную точку X, лежащую между X₁ и Х₂ на соединяющем их отрезке. Она принадлежит V (так как U выпукло), ее координаты есть x_j = ax_j1 + (1 - a)x_j2 (j = 1,..,n) и ей отвечает допустимое решение (1.7), имеющее вид

Очевидно, x_j, x_n+i могут формально рассматриваться как координаты точки X, находящейся на отрезке, соединяющем X̄₁ = (x_j1, x_n+i,1) и X̄₂ = (x_j2, x_n+i,2). Поскольку X выбирается произвольно, приходим к выводу: каждой не крайней точке X̄ из U можно поставить в однозначное соответствие не крайнюю X с координатами, представленными в виде линейной комбинации (1.8); следовательно, и каждой крайней X из U отвечает крайняя X̄.

Пусть теперь x_n+1 = В_i (i = 1,...,m), x_j = 0 (j = 1,..,n) - допустимое базисное решение системы (1.7), причем каждая его компонента задана как (1.8). Для номеров i = 1,...,n это означает 0 = ах_j1 + (1 - a)x_j2 или (с учетом требований не отрицательности переменных) x_j1 = 0, х_j2 = 0 при 0 < a <1, что приводит и к совпадению величин x_n+i, x_n+i,1 x_n+i,2. Таким образом, попытка представить компоненты базисного решения в виде (1.8) при x_j1 ≠ x_j ≠ x_j2 не удается, а само оно (согласно выводам первой части доказательства) определяет в U крайнюю точку □.

Доказанная теорема подводит в какой-то мере итог тем оценкам свойств задачи линейного программирования, которые были даны в § 1.1, 1.2, и позволяет утверждать следующее: если задача (1.2) имеет оптимальное решение, то существует хотя бы одно оптимальное базисное решение. Симплекс-метод может быть определен теперь как метод, предполагающий последовательный анализ базисных решений системы (1.2).

Реализация этой идеи требует в общем случае:

а) получения исходного допустимого базисного решения системы (1.2), если оно существует (или подтверждения факта неразрешимости указанной системы);

б) проверки полученного решения на оптимальность;

в) организации перехода к новому допустимому базисному решению, если предыдущее решение оказалось не оптимальным;

г) повторения операций б), в) до тех пор, пока не будет получено оптимальное базисное решение системы (1.2) (или подтверждена возможность неограниченного возрастания |z|).

Для многих практических задач удается сравнительно легко найти соответствующую каноническую форму (1.4) представления условий, но часто это вызывает трудности. Можно, конечно, предварительно исследовать вопрос существования решений, однако желательно, чтобы сам метод исключал необходимость таких исследований, т. е. не был бы связан с априорными предположениями о свойствах систем вида (1.2). Симплекс- метод удовлетворяет поставленным требованиям; он состоит из двух этапов, первый из которых является как бы вспомогательным (хотя и очень важным). Для этого этапа характерно следующее: начальные действия производятся с системой (1.2), входящей составной частью в стандартную форму задачи, причем не нужно ничего знать об этой системе или предварительно ее преобразовывать; в результате либо окажется найденным исходное базисное решение системы (1.2), либо последует вывод об отсутствии решения рассматриваемой задачи линейного программирования [см. п. а)].

Если возможность решения подтверждена, начинается второй этап реализации симплекс-метода, приводящий к отысканию экстремума г. Важно заметить, что основу обоих этапов составляет так называемый симплекс-алгоритм предусматривающий проведение ряда операций [см. п. б), в), г)] применительно к системе уравнений в канонической форме (на первом этапе приходится иметь дело с искусственной канонической системой).