1.6. Целочисленные решения линейных задач. Метод Гомори
Задачи, сформулированные в терминах линейного программирования и содержащие требование "все или некоторые xj - целые числа", играют важную роль в исследованиях различных прикладных проблем. Появление указанного требования приводит к пересмотру некоторых геометрических представлений, развитых в § 1.2. В первую очередь это относится к области определения задачи, которая отождествляется теперь с совокупностью дискретных точек - узлов целочисленной решетки (если все xj целочисленны) или с набором не пересекающихся линий, плоскостей и т. п. (см. рис. 1.7). Соответствующие коррективы приходится вносить и в методологию поиска оптимальных решений, причем серьезные трудности вызывает разработка теоретически обоснованных методов получения X*, 2*. Наибольший интерес представляет метод Гомори, краткая характеристика которого сводится к следующему:
- позволяет решать как частично, так и полностью целочисленные задачи линейного программирования;
- применим и в тех случаях, когда требование цело- численности распространяется на величину z;
- дает решение за конечное число шагов, т. е. предлагает определенную вычислительную процедуру (часто используется термин "алгоритм Гомори").
Обратимся к задаче: найти х1,х2 ,...., xn → min
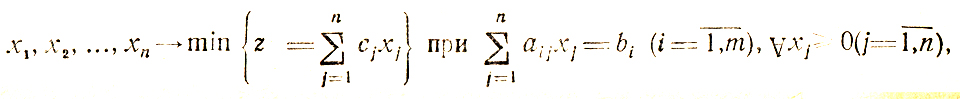
z и некоторые xj - целые числа (множество номеров этих xj обозначается в дальнейшем "J", так что принадлежность отдельно взятого j к J означает требование целочисленности для соответствующего xj).
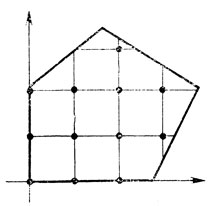
Рис. 1.7
Первый шаг алгоритма Гомори предусматривает отбрасывание условий "z, xj (j∈J) - целые числа" и решение задачи линейного программирования. В результате отыскивается каноническая система, например:
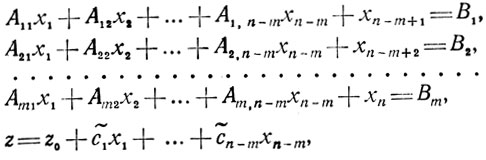 (1.15)
(1.15)указывающая оптимальное базисное решение:
x̂n-m+1 = B1,...., x̂n = Bn; x̂1 = ... =x̂n-m = 0 (1.16)
причем ∀Bj ≥ 0, ∀c̃j ≥ 0 (i = 1,...,m; j = 1,...,n). Для удобства дальнейших исследований вводится параметрическая форма представления компонент (1.16), получаемая из (1.15)
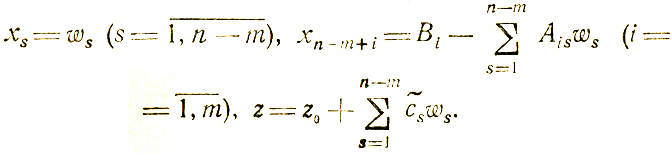
Упорядочение записи выражений всех переменных достигается здесь за счет использования единых обозначений коэффициентов при ws и свободных членов Bi, так что (1.15) переходит в
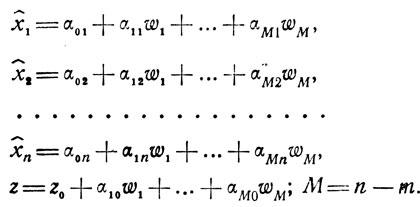 (1.17)
(1.17)Если (1.17) дает целые значения ẑ и x̂j(j∈J) при ∀ws = 0(s = 1,...,M), то исходные условия рассматриваемой целочисленной задачи удовлетворены. Если же этого нет (какие-то из α0j (j∈J) в 1,17 и, возможно, z0 оказались дробными), то необходимо продолжить поиск X*, г*, сделав второй шаг решения.
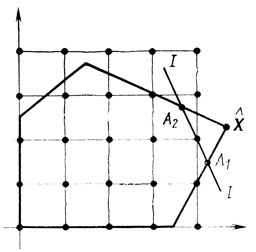
Рис. 1.8
Пусть либо z0, либо α0j (j∈J) есть дробные числа, т. е. равенства (1.17) определяют в области U стандартной задачи крайнюю точку X̂, которая не может быть принята в качестве X*. Возникает вопрос: нельзя ли так видоизменить область U, чтобы оказавшаяся ненужной точка X была отброшена, но все точки Х ≠ X̂, претендующие на роль X*, были сохранены? Ясно, что инструментом отсечения X̂ может стать дополнительное линейное ограничение, которому не удовлетворяют координаты X. На рис. 1.8 показана область U и некоторая гиперплоскость I - I, заданная дополнительным ограничением; здесь возникают новые крайние точки A1, А2. Такими построениями завершается второй этап реализации алгоритма Гомори.
Третий шаг предусматривает возвращение к задаче с отброшенными условиями целочисленности xj (j∈J) но с расширенной системой ограничений nΣj=1 aijxj = bi (i = 1,..., m + 1), в которую включено теперь то, что получено на втором шаге. Снова решается задача линейного программирования в стандартной постановке, и определяется новая точка X̂ (ей может стать, например, А1 на рис. 1.8).
Если найденная таким образом точка X̂ опять окажется ненужной, формируется новое (второе по счету) дополнительное ограничение, т. е. проводится четвертый шаг решения, повторяющий полностью второй шаг. Чередование подобных операций продолжается до тех пор, пока очередная точка X̂ не удовлетворит всем условиям исходной целочисленной задачи.
Из приведенного общего описания метода Гомори следует, что его отличительной особенностью являются периодические изменения конфигурации первоначальной области U с целью ее сужения. Именно здесь оказывается удобным представление компонент x̂j оптимального решения стандартной линейной задачи в виде (1.17), поскольку равенства (1.17) используются непосредственно для формирования отсекающих ограничений.
Чтобы перейти к соответствующим формализмам, введем следующие понятия и обозначения:
[β] - наибольшее целое число, не превосходящее β;
fβ = β - [β] - положительная собственная дробная часть числа β;
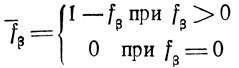
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'