1.7. Формирование дополнительных ограничений

Принципы формирования дополнительных ограничений основываются на результатах теорем, приводимых ниже. Теорема (5): если x̂_j - переменная, на которую распространяется требование целочисленности, w_s(s = 1,...,М) -параметры, связанные с x̂_j соотношением x̂_j = α_0j + α_1jw₁ + .... +α_Mjw_M, если ∀α_sj (s∈1,...,M), то линейное неравенство

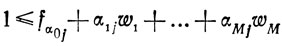(1.18)

выполняется для всех w_s, дающих целочисленное x̂_j, и не выполняется для базисного решения (1.16), получаемого из (1.17) ∀w_s = 0, s = 1,...,M.

Доказательство: вследствие не отрицательности (по предположению) величин α_sj и w_s (s = 1,...,M) минимальное значение x̂_j не может быть меньше α_0j, т. е. min x̂_j ≥ α_0j - отсюда следует x̂_j ≥ [α_0j] + 1 поскольку x̂_j есть целое число. Вычитая это неравенство из выражения x̂_j, приведенного в условии теоремы, приходим к соотношению (1.18), что и доказывает первую часть утверждения теоремы; доказательство второй части очевидно: f_α0j ≤ 1 всегда (по определению f).□

Полученный результат легко преобразуется в дополнительное ограничение, используемое в методе Гомори.

Если записать условие x̂_j[α_0j] + 1 в виде равенства x̂_j - x̂̂_j = [α_0j] + 1 (для этого переменная x̂̂_j должна быть не отрицательной и целочисленной) и вычесть это равенство из выражения x̂_j, то

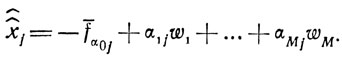(1.19)

Выбрав x̂̂_j в качестве новой переменной и дополнив систему (1.17) уравнением (1.19), приходим к следующему: при обращении всех ws в нуль (этим определяется точка X) появится базисное решение

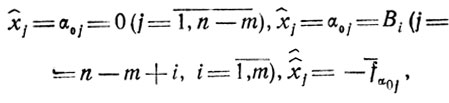
в котором одна переменная (именно x̂̂_j) отрицательна, поскольку всегда f̄_α0j > 0. Такое решение недопустимо,

следовательно, условие (1.19) не удовлетворяется в точке X̂, хотя во всех других точках, для которых рассматриваемая координата %j принимает целочисленные значения, оно выполнено (это следует из равенства x̂̂_j = x̂_j - [α_0j] - 1, дающего целые неотрицательные значения x̂̂_j при любом x̂_j ≥ [α_0j] + 1).

Таким образом, уравнение (1.19) может быть использовано для расширения системы (1.17) с целью отсечения X̂. Известным недостатком, ограничивающим область применения теоремы (5), является введенное выше требование не отрицательности коэффициентов α_sj (s = 1,...,M; j∈J). Чтобы избежать связанных с этим неудобств, обратимся к доказательству еще одной теоремы (6): если x̂_j (1≤j≤n, j∈J) и w_s (s = 1,....,М) - целочисленные неотрицательные переменные, такие, что x̂_j = α_0j+^MΣ_s=1 α_sjw_sлинейное неравенство

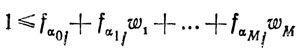
выполняется для всех w_s, дающих целое значение и не выполняется для базисного решения (1.16), получаемого из (1.17) при нулевых w_s.

Доказательство: каждая величина α_sj (s = 0,...,М) в выражении x̂_j может быть представлена как α_sj = [α_sj]+f_αsj тогда само выражение x̂_j принимает вид

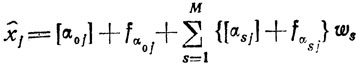
или после несложных преобразований

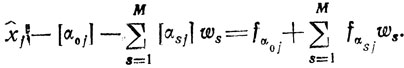
Левая часть этого равенства есть целое число вследствие целочисленности (по предположению) всех w_s и x_j, кроме того, все f_αsj неотрицательны, что позволяет

отождествить возникшие здесь условия с условиями теоремы (5) (разница лишь в обозначениях коэффициентов при w_s и переменной, стоящей в левой части). Следовательно, выводы теоремы (5) доказывают утверждения теоремы (6). □

Так же, как и в предыдущем случае, здесь можно ввести в рассмотрение целочисленную неотрицательную величину x̂̂_j, определяемую выражением

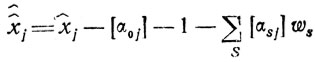
или

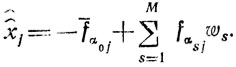(1.20)

Добавление уравнения (1.20) в систему (1.17) обеспечивает отбрасывание X̂ и не затрагивает точек, для которых координата x̂_j остается целочисленной.

Теорема (6) тоже должна иметь ограниченную область применения из-за условия "все w_s - целые числа", однако всегда существует возможность объединения результатов (1.19) и (1.20).

Теперь остается рассмотреть общий случай, когда переменные ws могут быть и дробными, и целочисленными, а коэффициенты asj при дробных ws не имеют ограничений на знак. Для упрощения формулировок введем следующие обозначения:

S₁ - множество номеров s, для которых w_s - целые и α_sj>0;

S₂ - множество номеров s, для которых w_s - дробные и α_sj>0;

S₃ - множество номеров s, для которых w_s - целые и α_s<0;

S₄ - множество номеров s, для которых w_s - дробные и α_sj<0.

Существует теорема (7): если x̂_j - переменная, на которую распространяется требование целочисленности, и w_s - параметры, связанные с x̂_j соотношением x̂_j = α_oj+^MΣ_s=1 α_sjw_s, то линейное неравенство

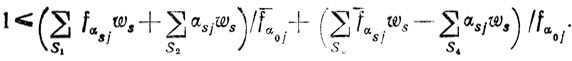
выполняется для всех w_s, дающих целочисленное x̂_j, и не выполняется для базисного решения (1.16), получаемого из (1.17) при ∀w_s = 0.

Не останавливаясь подробно на доказательстве, обратим внимание на важное обстоятельство: переменная x̂̂_j, заданная здесь как

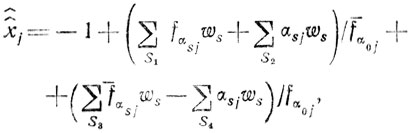
не обладает свойством целочисленности в отличие от (1.19) и (1.20); будучи введенной в систему (1.17), она не может использоваться на последующих шагах для формирования новых ограничений и лишь увеличивает размерность задачи. Следовательно, всегда имеет смысл обращаться к результатам теорем (5) или (6) (если это допускают условия конкретной задачи). Дополнительные пояснения дает следующий пример.

Пример: найти x₁ ..., x₄→min{-7/12+x₁/4+4x₃/3} при условиях: x₁, x₂, x₃, x₄ - целые неотрицательные числа, z - целое число и 2х₁+x₂+4x₃/3 = 13/3; x₁/2+3x₃+x₄ = 9/4.

Решение: отбрасывая требование целочисленности x_j(j = 1,...,4) и z, видим, что оптимальное решение стандартной задачи линейного программирования можно указать сразу - x̂₁ = 0, x̂₂ = 13/3, x̂₃ = 0, x̂₄ = 9/4, z = -7/12; следовательно, положив x̂₁ = w₁ и x̂_s = w₃, получим из исходных условий систему типа (1.17):

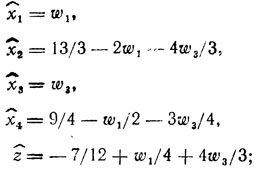(I)

свободные члены второй, четвертой и пятой строк (I) являются дробными, и необходимо ввести дополнительное ограничение; для его формирования удобно выбрать строку ẑ, где α_0j = α_0z = -7/12 и f̄_α0i = 7/12; согласно рекомендациям теоремы (5) новая переменная (обозначаемая просто x̂₅) определяется равенством x̂₅ = -7/12+w₁/4+w₃/3, а расширенная система ограничений принимает вид

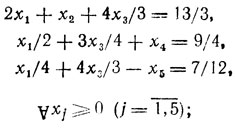(II)

ясно, что x̂₁ и x̂₂ не могут оставаться свободными (при x̂₁ = x̂₃ = 0 величина x̂₅ отрицательна); чтобы найти им замену, обратимся к задаче: найти x₁, х₂,....,х₅→min{z = x₅} при ограничениях (II); ее решением являются x̂₁ = 45/21, x̂₂ = 0, x̂₃ = 1,28, x̂₄ = 129/112, x̂₅ = 0 или (в параметрическом представлении)

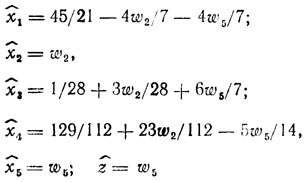(III)

(полезно обратить внимание на то, что здесь ẑ = 0; отбрасывание

очередной точки X̂ может сопровождаться увеличением ẑ, и совсем не исключено, что оптимальное решение исходной целочисленной задачи может оказаться хуже - в смысле полученной величины z, - чем решения промежуточных задач); в строках системы (III) опять присутствуют дробные свободные члены, поэтому нужно вводить новое дополнительное ограничение; выбрав строку x̂₃ с α₀₃ = 1 /28 и f_α03 = 27/28, получаем x̂₆ = -27/28+3w₃/28+6w₅/7; отсюда следует формулировка третьей по счету линейной задачи - найти x₁, х₂,..., x₆→min{z = x₅} при

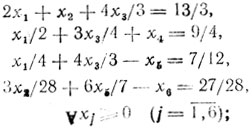(IV)

решив ее, получаем x̂₁ = 0, x̂₂ = 3, x̂₃ = 1, x̂₄ = 3/2, x̂₅ = 3/4, x̂₆ = 0 или

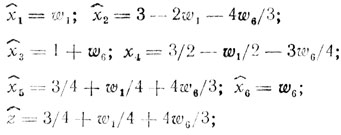(V)

результат (V) не удовлетворяет исходным требованиям целочисленности всех x_j(j = 1,...,6), и в качестве еще одного ограничения, порождаемого строкой x̂₅ в (V), принимается x̂₇ = -1 /4+w₁/4+w₆/3; это приводит к очередной линейной задаче - найти x₁,....,x₇→min {z = x₅} при

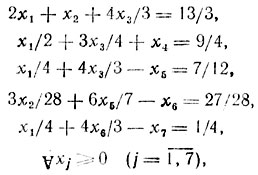(VI)

и решению x̂₁ = 1, x̂₂ = 1, x̂₃ = 1, x̂₄ = 1, x̂₅ = 1, x₆ = 0, x̂₇ = 0, ẑ = 1, которое полностью целочисленно и должно быть признано оптимальным для исходных условий, т. е. x^*₁ = 1, х^*₂ = 1, х^*₃ = 1, x^*₄ = 1, z^* = 1.