2.5. Теорема Милютина-Дубовицкого. Интерпретации общих условий экстремума

Остается выяснить, при каких условиях пересечение

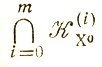
окажется пустым. Ответ на "этот вопрос дает теорема Милютина-Дубовицкого.

Пусть R̃ - эвклидово пространство размерности (m+1)n (оно может быть образовано как прямое произведение m+1 пространств R_(n)i предварительно пронумерованных). Произвольный вектор Z∈R̃ определяется совокупностью векторов Х_(i), принадлежащих соответствующим R_(n)i (i = 0,....,m), а его проекциями на координатные оси в R_(n)s являются x_js (j = 1,....,n; 0≤s≤m).

Вектор X_(s)∈R_(n)s с составляющими x_js может быть назван R_(n)s - компонентой Z,

Все X_(s), представляемые в виде суммы Х° + ρ_δ^(s)δ(s) (s) (0≤ρ_δ^(s)≤ρ^(s)) составляют множество R^(s)_X° все Z, компоненты X_(s) которых принадлежат только R^(s)_X°, образуют множество R̃_X°, включенное в R̃; наконец, все Z, имеющие равные компоненты X_(s) (s = 0,....,m), образуют выпуклое множество П. Если пересечение конусов пусто, то пусто и пересечение множеств R^(s)_X°.

Предположим, что

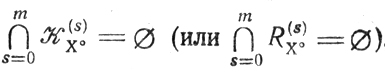
Отсюда следует: множества Π и R̃_X° не имеют общих элементов (если бы существовал хотя бы один такой элемент точка Z, все ее R_(n)s -компоненты принадлежали бы R^(s)_X°, оставаясь равными между собой; по это означало бы существование элемента, входящего во все R^(s)_X°, что противоречит рассматриваемому предположению).

Поскольку два выпуклых множества Π и R̃_X° не имеют общих точек, их можно разделить. Другими словами в R̃ найдется такой вектор А≠0 с R_(n)s-компонентами A(s), что (A, Z_R) > (A, Z_n) для любых Z_R ∈ R̃_X° и Z_Π ∈ Π.

Это неравенство можно переписать в виде

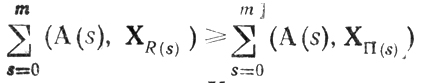
или, учитывая форму представления X_(s),

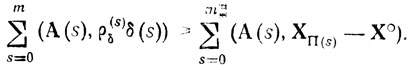(2.10)

Рассматриваемые соотношения имеют место при любых Х_П(s) и любых неотрицательных ρ_δ^(s), меньших или равных ρ^(s), поэтому можно положить Х_Π(s) = Х°, ρ_δ^(s) = ρ^(s) для s = p (0≤p≤m), ρ^(s) = 0 для s≠p. Следовательно, (A(р), δ(р) за 0 для произвольного δ(р)∈K^(p)_X° и А(р)∈K^(p)*_X°

Неравенство (12.10) должно выполняться и тогда, когда ∀ρ^(s)_δ (s = 0,...,m);

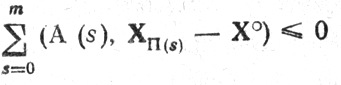
или

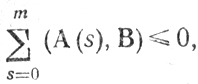
где В = Х_П(s) - Х° - вектор, не зависящий от s вследствие равенства всех Х_П(s) (они являются компонентами вектора Z_Π ∈ П), В свою очередь,

неравенство

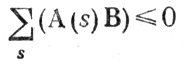
справедливо для любых том числе и для

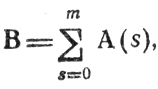
но это возможно лишь при

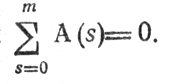
Таким образом, получены условия существования в точке X°∈U минимума функции f(X), что находит отражение в уже упоминавшейся теореме Милютина-Дубовицкого (10): для того, чтобы множество

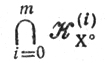
было пустым, необходимо существование таких векторов А(i), принадлежащих соответствующим K^(i)*_X°которые удовлетворяли бы условию

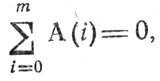
не будучи все равными нулю.

Ясно, что терминология формулировок может меняться в зависимости от конкретного содержания исследуемой оптимизационной задачи. В этом смысле представляют интерес возможные интерпретации рассмотренных понятий применительно к частным случаям.

Пусть выпуклые множества Ui определяются условиями g_i(X)≤b_i (i = 1,.....,m) или просто φ_i(Х)≤0, где φ_i(X) - дифференцируемые функции (функция f(X) тоже считается дифференцируемой). Пересечение U = ∩_i U_i (область определения задачи) не пусто, т. е. задача является содержательной. Исследуем сначала конус K⁽⁰⁾_X°.

Вдоль всех направлений, его составляющих, f(X) убывает, поэтому (df/de)_X° = (∇f, е)<0, при е∈K⁽⁰⁾_X° (другими словами, K⁽⁰⁾_X° объединяет такие векторы е, что(∇f, е)<0). Сопряженный конус K^(0)*_X° объединяет точки (векторы) А₀, удовлетворяющие условию (А₀, е) > 0. Следовательно, А₀ = λ₀∇f при λ₀≤0 (произвольному А, соответствует не положительное число λ₀). Относительно K⁽ⁱ⁾_X° (i = 1,....,m) можно заметить следующее: если Х° является внутренней точкой области U_i, то конус K⁽ⁱ⁾_X° совпадает с R_n; если же Х° есть граничная точка U_i, то конус K⁽ⁱ⁾_X° содержит векторы е, образующие тупой угол с направлением (∇φ_i)_X°. (см. рис. 2.11), т. е. e∈K⁽ⁱ⁾_X° при (∇φ_i(Х°), е)<0, а сопряженный :конус образуют векторы A_i = λ_iφ_i (Х°) при λ_i<0 (эти условия могут быть интерпретированы и так: если A_i∈K⁽ⁱ⁾_X°^*, то либо А_i=0 при φ_i(Х°)<0, либо А_i = λ_iφ_i(Х°), λ_i<0 при φ_i(Х°) = 0). Отсюда следует другая формулировка теоремы (10): для того чтобы f(X) достигала минимума в точке Х° при ограничениях φ_i(Х)≤0, необходимо существование таких чисел λ_i≤0, (t = 1,....,m), которые, не будучи все равными нулю, удовлетворяли бы условиям

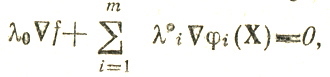
причем λ_i=0 при φ_i(X)<0.

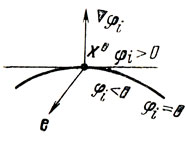
Рис. 2.11

В этой формулировке рассматриваемая теорема совпадает с правилом множителей Лагранжа. Оказывается, при определенных условиях она приводит и к теореме Куна-Таккера.

Пусть X^* -точка минимума вогнутой функции f(X) на выпуклом непустом множестве

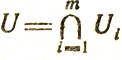
заданном ограничениями φ_i(X)≤0, где φ_i - выпуклые функции. Очевидно, X^* удовлетворяет требованиям теоремы (10), например, в ее последней формулировке, из которой следует

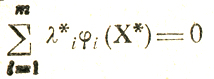
(всегда либо φ_i(Х^*) = 0, либо соответствующий множитель λ_i^*, обращается в нуль). Таким образом, для любого λ_i≤0 имеем

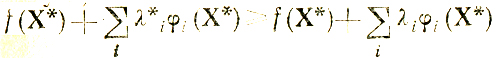
или Φ(Х^*,Λ^*)≥Φ(Х^*,Λ), где Φ - функция [Лагранжа. Вместе с тем, в силу вогнутости (по предположению) функций f(X), λ_iφ_i(Х) (λ_i≤0, i = 1,...,m) вогнутой по X оказывается и Φ(Х, Λ), что позволяет утверждать Φ(Х, Λ^*)≥Φ(Х^*, Λ^*) (равенство ∇Φ = 0 предполагается выполненным в силу требований теоремы Милютина - Дубовицкого). Полученные соотношения указывают на существование седловой точки X^*, Λ^* функции Лагранжа как необходимое и достаточное условие экстремума f(X) в рассматриваемом случае.

Общие подходы к проблемам поиска экстремума создают предпосылки для дальнейших исследований теории и прикладных методов математического программирования. Не теряют своего значения и результаты, полученные применительно к отдельным классам задач.