2.4. Проблема единого подхода к задачам математического программирования. Условия существования оптимума
Поиски более общих условий экстремума (по сравнению с рассмотренными в п. 2.3) приводят к необходимости использования новых понятий, не встречавшихся ранее. Обратимся к определениям:
- множество K называется конусом с вершиной в начале координат, если вместе с точкой (вектором) X оно содержит и точки (векторы) аХ, а≥0;
- двойственным (или сопряженным) данному K называется конус K*, содержащий те точки (векторы) Y, которые удовлетворяют условию (Y, Х)≥0, ∀X∈K, где (Y, X) - скалярное произведение указанных X, Y (см. рис. 2.4; конус K* заштрихован);
- Многогранным конусом, образованным на базе векторов Vp, называется множество векторов X, получаемых
как Х = NΣp=1 арVр при ∀ai≥0 (рис. 2.5);
- конусом возможных направлений KХ0, рассматриваемым по отношению к некоторому выпуклому множеству U и связанным с произвольной точкой Х0∈U, называется совокупность всех отличных от нуля векторов 8, каждому из которых можно поставить в соответствие такое число ρδ>0, что X=Х0+ρδδ будет принадлежать U пои любом 0<ρδ≤ρ, ρ>0 (см. рис. 2.6; здесь KX0 образован векторами X - Х0, составляющими с касательной угол, не превышающий π);
- конусом возможных направлений KfX0, рассматриваемым по отношению к некоторой функции f(X) и связанным с Х0, называется совокупность 8^0, каждому из которых можно поставить в соответствие такое число ρδ>0, f(X0+ρδδ)≤f(X0) при любом 0<ρδ≤ρ, ρ>0 (другими словами, KfX0 содержит точки X, в которых значения f не превышают f(X0)).
Рассмотренные определения позволяют сформулировать ряд теорем, которые используются в дальнейшем для исследования свойств экстремума f(X).
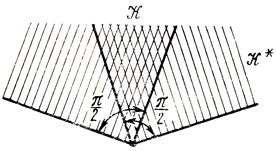
Рис. 2.4
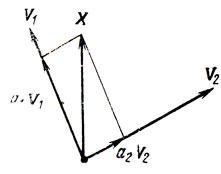
Рис. 2.5
I. Если U - замкнутое выпуклое множество и Y - внешняя по отношению к U точка, то существует единственная точка Х0∈U, обладающая свойством ||Х0-Y||<||X-Y|| для ∀ Х∈U, Х ≠ Х0 (действительно, величина ||X-Y|| является непрерывной неотрицательной функцией X, и на произвольном замкнутом множестве она достигает своего минимума ||X0-Y||; поскольку U выпукло, Х0 - единственна, см. рис. 2.7).
II. Если U - выпуклое замкнутое множество и Y - внешняя по отношению к U точка, то существует такой вектор А, что (А, Х)<(А, Y) для ∀X∈U (первая теорема о отделимости).
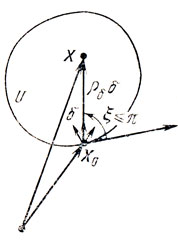
Рис. 2.6
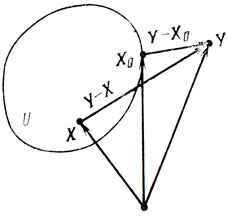
Рис. 2.7
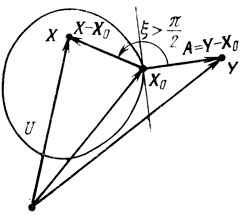
Рис. 2.8
Доказательство: пусть X - произвольная точка области U; тогда Q∈U, если Q = aX+(1-a)X0, 0<а<1 (свойство выпуклости U), и в силу утверждения I выполнено неравенство ||Y-X0||2<||Y-Q||2, которое может быть - интерпретировано как (Y-Х0, Y-X0) < (1-а) Х0-аХ, Y-(1-а) Х0-аХ) или а2-2а(Х-Х0, Y-X0)>0, скольку все эти соотношения должны иметь место и при сколь угодно малых а>0, необходимо (X-Х0, Y-Х0) < 0; положив Y-Х0 = А, получим (Х-Х0, А) < 0 или (А, Х)<(А, Х0) и тем более (А, X)<(А, Y) (см. рис. 2.8); из условия (А, X)<(А, Y) следует (kA, X) < (kА, Y), k>0, поэтому без потери общности можно принять ||А|| = 1. □
III. Если U1, U2 - выпуклые замкнутые множества, не имеющие общих точек, то существует такой вектор А, что (А, Х)<(А, Y) для ∀ X∈U1 и ∀Y∈U2 (вторая теорема об отделимости).
Доказательство: пусть P - множество точек Р = Х-Y при Х∈U1 ,Y∈U2; можно показать, что P выпукло в рассматриваемых условиях; кроме того, всегда можно считать точку 0 внешней по отношению к Р; следовательно, существует вектор А, для которого (А, Р)<(А, 0) или (А, X-Y)<0; последнее неравенство равносильно утверждению (А, Х)><(А, Y) (см. рис. 2.9). □ Геометрический смысл этого результата заключается в возможности провести некоторую разделяющую гиперплоскость, так что области U>1 и U2 окажутся "по разные стороны" от нее (приведенную теорему обычно называют теоремой об отделимости двух выпуклых множеств) .
Непосредственное использование введенных выше понятий связано с рассмотрением важной теоремы (9): если Х°∈U есть точка минимума функции f(X) и множество U выпукло, то пересечение конусов KfX° и KX° пусто.
Доказательство: пусть рассматриваемое пересечение не пусто и X̂ есть произвольная точка, ему принадлежащая; если Х° является внутренней экстремальной точкой, то KX° совпадает с U и X̂∈KfX°∩U (рис. 2.10); из факта принадлежности X̂ множеству KfX° следует f(Х̂)<f(Х°) (см. определение Kfx°), т. е. Х° не доставляет минимума f(X) (возникшее противоречие доказывает исходное утверждение); аналогичная ситуация возникает и в случае, когда Х° лежит на границе U (см. рис. 2.10). □
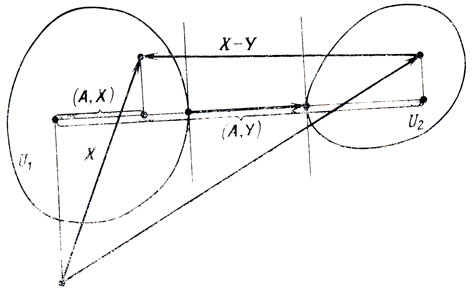
Рис. 2.9
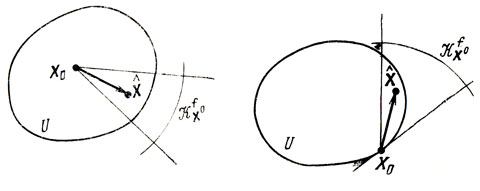
Рис. 2.10
Обычно область U представляется как пересечение нескольких областей Ui, порождаемых отдельными ограничениями, входящими в систему вида gi(Х)≤bi или φi(Х)≤0, т. е.
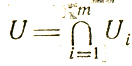
Пусть Ui выпуклы; обозначив конус возможных направлений, относящийся к Ui как K(i)X° конус KfX° как K(0)X° приходим к заключению: f(X) достигает минимума в X°∈U если
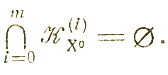
Сайт https://uzhnosahalinsklust.com регулярно обновляет анкеты, чтобы у пользователей был актуальный выбор.
|
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'