2.7. Метод Вольфа в квадратичном программировании

Идея метода Вольфа в общих чертах такова: вводятся дополнительные переменные, позволяющие перейти от системы (2.12) к новой системе уравнений, для которой легко указать базисное решение, допустимое с точки зрения требований x^*_jp^*_j = 0 (j = 1,...,n) и λ^*_iq^*_i = 0 (i = 1,...., m); решается задача линейного программирования с целью обратить эти переменные в нуль (т. е. возвратиться к исходной системе 2.12, но так, чтобы получить при этом оптимальное базисное решение, определяющее X^*). В процессе такого перехода все время приходится следить за соблюдением условий x^*_jp^*_j = 0 и что и определяет единственное отличие применяемого здесь симплекс-алгоритма от того, который известен в линейном программировании.

Метод Вольфа разработан в двух вариантах. Частный вариант метода позволяет получить решение задачи либо тогда, когда квадратичная форма, входящая в выражение z, является отрицательно определенной (т. е

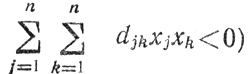
либо тогда, когда ∀c_j = 0 (j = 1,....,n).

Общий вариант дает возможность решить задачу без этих оговорок, но он более громоздкий, так как в нем дважды повторяется схема частного варианта, которая и будет рассмотрена здесь.

Введем в (2.12) искусственные неотрицательные переменные y_i (i = 1,....,), w'_j (j = 1,...., n), w"_j (j = 1,...,n) так, что

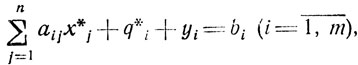(2.13)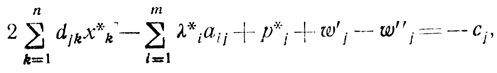

Для системы (2.13) можно сразу назвать базисное решение, удовлетворяющее условиям: не более n+m переменных отличны от нуля, выполнены требования x^*_jp^*_j = 0 (j = 1,....,n), λ^*_iq^*_i = 0 (i = 1,....,m). Таким решением является либо x^*_j = 0, p^*_j = 0, λ_i^* = 0, q^*_i = 0, w"_j = 0, y_i = b_i, w'_j = c_j (при ∀c_j>0), либо x^*_j = 0, p^*_j = 0, λ_i^* = 0, q^*_i = 0, w'_j = 0, y_i = b_i, w"_j = с_j (при ∀c_j>0). Если ∀ c_j = 0 (j = 1,...,n), то безразлично, какое из названных решений использовать. Важно подчеркнуть, что такие решения не являются допустимыми для (2.12) и могут выступать лишь в качестве исходных в задачах линейного программирования, рассматриваемых ниже.

Первый этап реализации метода Вольфа предусматривает решение следующей вспомогательной задачи: найти

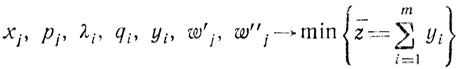
при ограничениях (2.13). Ясно, что минимизация суммы неотрицательных y_i (i = 1, ...,m) должна привести к отысканию базисного решения, содержащего нулевые компоненты y_i (i = 1,...,m) и удовлетворяющего поэтому "промежуточной" системе уравнений

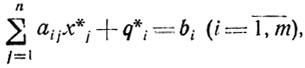(2.14)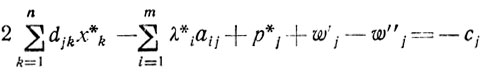

Теперь можно отбросить все y_i (они обращены в нуль), те w'_j, которые входят в строки с c_j>0, и те w"_j, которые входят в строки с c_j<0 (нужно оставить в каждой строке либо w'_j, либо w"_j в зависимости от знака соответствующего c_j). Тем самым число переменных группы w сокращается до n, и появляется возможность сделать следующий шаг, направленный на окончательное их исключение.

Второй этап реализации метода Вольфа связан с решением следующей задачи: найти p_j, h_i, λ_i, q_i,

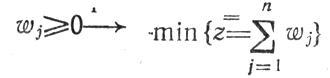
при ограничениях (2.14). Оно проводится с соблюдением правила: при переходе к очередному базисному решению переменная p_j(x_j) не должна включаться в базис, если там уже находится x_j(p_j) (запрещается одновременное пребывание x_j и p_j с одинаковым номером у в числе переменных, отличных от нуля). Если min z̄̄ = 0, то соответствующее оптимальное базисное решение является одновременно и решением системы (2.12), т. е. всей задачи квадратичного программирования. Этим заканчивается вычислительная процедура, составляющая содержание метода Вольфа.

Выше было замечено, что рассмотренный здесь частный вариант метода Вольфа применим в случае, когда либо ∀c_j = 0, либо

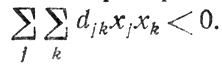
Если снять названные ограничения, может оказаться, что из-за требования обеспечить равенства x^*_jp^*_j = 0, λ^*_iq^*_i = 0 (j = 1,..., n; i = 1,...,m) переход от одного промежуточного базисного решения к другому будет невозможен, хотя z еще не обратится в нуль.

Ниже дан пример, иллюстрирующий возможности метода.

Пример: найти x₁, х₂→min{z = x₁ + 2x₂ - 0,5x²₁ - 0,5x²₂} при x₁,x₂≥0, 2x₁+3x₂≤6, x₁+4x₂≤5 (нетрудно видеть, что в роли слагаемого

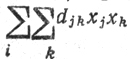
здесь выступает сумма -0,5x²₁-0,5x²₂, причем она отрицательно определена в U; следовательно, допустимо применение частного варианта метода Вольфа).

Решение: составляем функцию Лагранжа

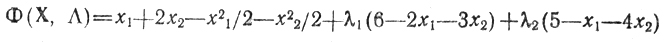
и находим

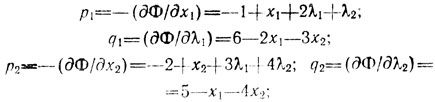
поскольку здесь c_j < 0 (j = 1, 2), можно ограничиться введением всего n+m искусственных переменных y_i (i = 1, 2), w"_j = w_j (j = 1, 2), и тогда первая задача линейного программирования принимает вид: найти x₁, х₂, p₁, р₂, λ₁, λ₂, q₁, q₂, y₁, y₂, w₁, w₂ минимизирующие

сумму z̄ = y₁+y₂ при условиях

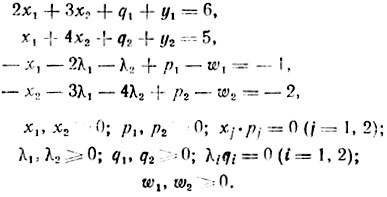(I)

Базисное решение системы (I), удовлетворяющее требованиям x_jp_j = 0 и λ_iq_i=0, можно назвать сразу: x₁ = x₂ = 0, p₁ = p₂ = 0, x₁ = x₂ = 0, q₁ = q₂ = 0, y₁ = 6, y₂ = 5, w₁ = 1, w₂ = 2; используя его в качестве исходного в решении сформулированной линейной задачи, выразим y_i, w_j (i = 1,2; j = 1,2) и z через свободные переменные

в соответствии с уравнениями (I), что дает

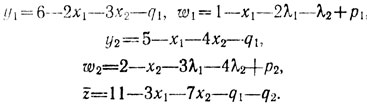
Если теперь увеличить, например, q₁ до 6 (при этом y₁ обращается в нуль), то можно получить новое допустимое базисное решение х₁ = х₂ = 0, р₁ = р₂ = 0, λ₁ = λ₂ = 0, y₁ = q₂ = 0, q₁ = 6; y₂ = 5, w₁ = 1, w₂ = 2. Выражения новых связанных переменных и г приобретают вид

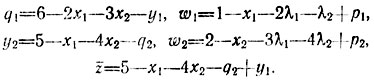
Увеличивая теперь q₂ до 5, т. е. обращая y₂ в нуль, имеем x₁ = x₂ = = 0, р₁ = р₂ = 0, λ₁ = λ₂ = 0, y₁ = y₂ = 0, q₁ = 6, q₂ = 5, w₁ = 1, w₂ = 2, z̄ = y₁+y₂.

Таким образом, достигнут минимум z̄ (не базисные переменные входят в выражение z̄ с положительными коэффициентами), и этот минимум оказался равным нулю, причем требования x_jp_j = λ_iq_i = 0 и λ_iq_i = 0 удовлетворены; именно возможность сохранять λ_i= 0 (i = 1,2) в процессе решения первой линейной задачи (это обеспечивается структурой выражений (I)) позволила избежать трудностей, связанных с необходимостью следить за соблюдением равенств λ_iq_i = 0. Последнее из полученных выше базисных решений, удовлетворяющее всем ограничениям (I) и минимизирующее z̄, построено так, что одновременно удовлетворяет и уравнениям (II), являющимся ограничениями во второй задаче линейного программирования: найти х₁, х₂, р₁, р₂, λ₁, λ₂, q₁, q₂, w₁, w₂ → min{z̄̄ = w₁ + w₂} при

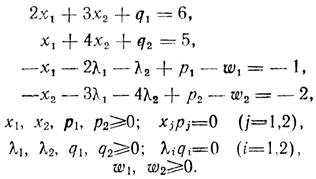(II)

Отсюда следует

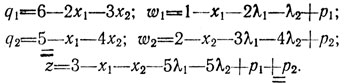
Нетрудно видеть, что добиться уменьшения z̄̄ можно за счет увеличения либо x_j, либо λ_i (j = 1,2; i = 1,2). Выбирая для этого переменную x₁ и увеличивая ее до единицы (при этом w₁ обращается в нуль), получаем базисное решение w₁ = x₂ = 0, р₁ = р₂ = 0, λ₁ = λ₂ = 0, q₁ = 4, q₂ = 4, x₁ = 1, w₂ = 2 и новые выражения

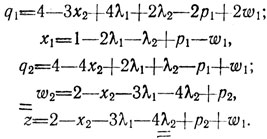
Ясно, что дальнейшее уменьшение z̄̄ должно сопровождаться возрастанием только х₂, так как при попытке увеличить λ₁ или λ₂ нарушаются равенства λ_iq_i = 0; величина х₂ может расти до единицы (при этом q₂ обращается в нуль), что приводит к решению w₂ = q₂ = 0, p₁ = p₂ = 0, λ₁ = λ₂ = 0, q₁ = 1, x₁ = 1, x₂ = 1, w₂ = 1 и выражениям

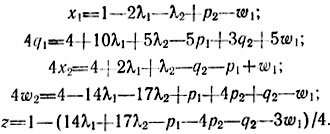
Теперь увеличивать можно лишь λ₂ (поскольку q₂ = 0), причем до значения 4/17 (w₂ обращается в нуль). Получаемое базисное решение w₁ = q₂ = 0, p₁ = р₂ = 0, λ₁ = w₂ = 0, q₁ = 22/17, x₁ = 13/17, х₂ = 18/17, λ₂ = 4/17 оказывается искомым, так как здесь 2 = 0 и удовлетворены все условия (II); таким образом, для исходной задачи квадратичного программирования имеем x^*₁ = 13/17, х^*₂ = 18/17.

В рассмотренном примере метод Вольфа выглядит довольно громоздким, однако его преимущество состоит в том, что он сводит процесс решения к последовательному применению симплекс-метода, который удобно реализовать с помощью ЭВМ. Вместе с тем известны и другие методы, основанные на интерпретациях условий Куна-Таккера, но их подробное изучение потребовало бы значительного увеличения объема данной главы.

В заключение обратимся к краткому исследованию вопроса о двойственных задачах квадратичного программирования. Таким задачам присущи характерные особенности, вытекающие из связи между их целевыми функциями и ограничениями.

В квадратичном программировании вопрос о двойственности начинает рассматриваться по существу вместе с изучением особенностей функции Φ(Х, Λ). Если нет требования не отрицательности x_j (j = 1,...,n) и Φ(Х, Λ) имеет минимум по Λ в точке X°, Λ°, то можно ставить задачу об отыскании совокупности значений λ°_i (i = 1,...,m), доставляющих минимум функции Φ(Х, Λ) при условиях

(dΦ/dx_j)_x°j = 0 (j = 1,...,n). Другими словами, задача: найти

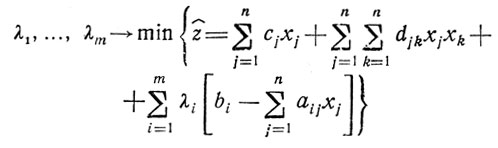
при

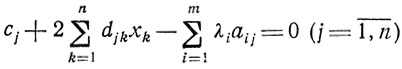
является двойственной по отношению к задаче: найти

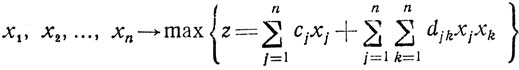
при

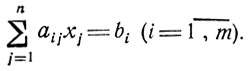
Обычно условия двойственности записываются здесь в несколько ином виде. Каждая строка-ограничение умножается на соответствующее x_j, и после суммирования по номерам j возникает равенство

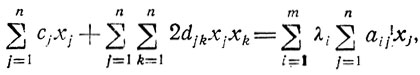
что позволяет формулировать двойственную задачу так: найти

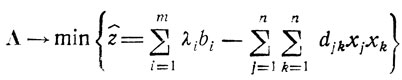
при

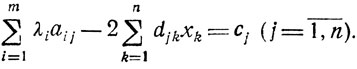
Если теперь ввести в указанную выше исходную квадратичную задачу требование ∀x_j>0 (j = 1,..,n) и учесть условие (dΦ/dx_j)_x°j ≤ 0, то двойственная задача принимает вид: найти

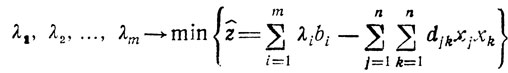
при

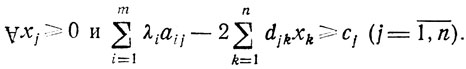
Вследствие своей несимметричности двойственные квадратичным задачи (они оказываются линейными относительно Λ) не получили столь широкого распространения, как аналогичные задачи, изученные в § 1.5. Это объясняется, в частности, следующим: если X^* есть решение прямой задачи (квадратичной), то компоненты X^* совпадают с соответствующими x^*_j, получаемыми из анализа двойственной (линейной) задачи; обратное утверждение верно лишь тогда, когда

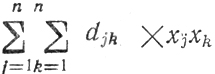
строго отрицательно (положительно) определена в U.